- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрия на ОГЭ
Содержание
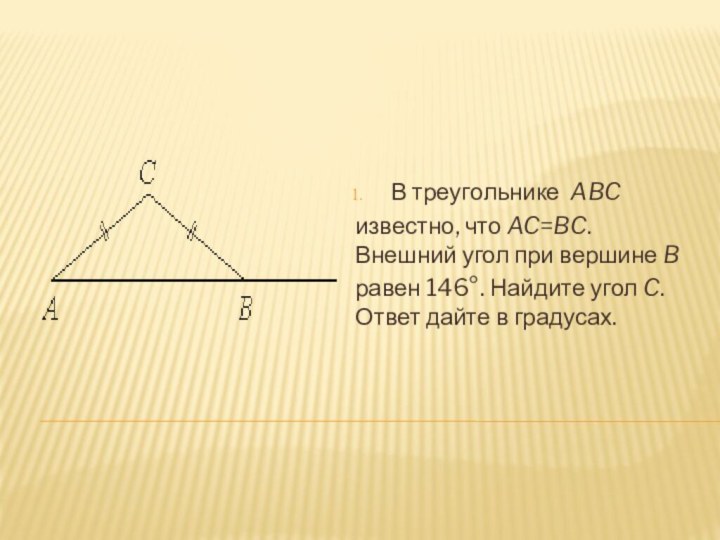
- 2. В треугольнике ABC известно, что AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.
- 3. 2. Какое из следующих утверждений верно?1) Площадь
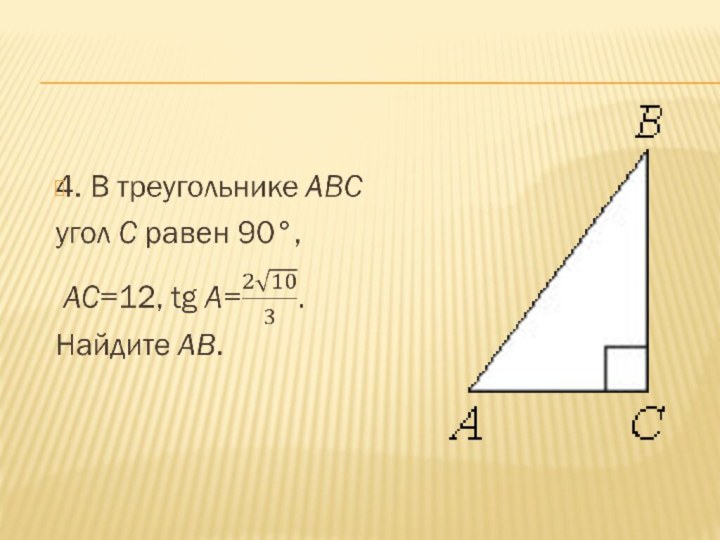
- 4. 3. Какое из следующих утверждений верно?1)Все углы
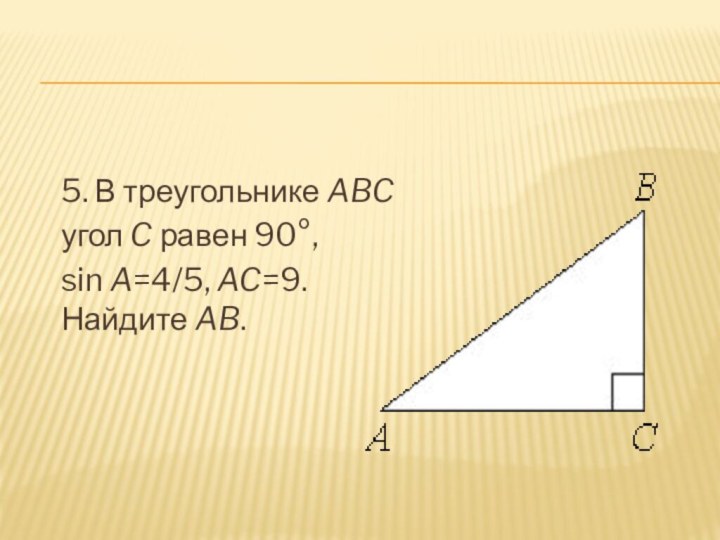
- 6. 5. В треугольнике ABC угол C равен 90°, sin A=4/5, AC=9. Найдите AB.
- 7. 6. Высота равнобедренной трапеции, проведённая из вершины C,
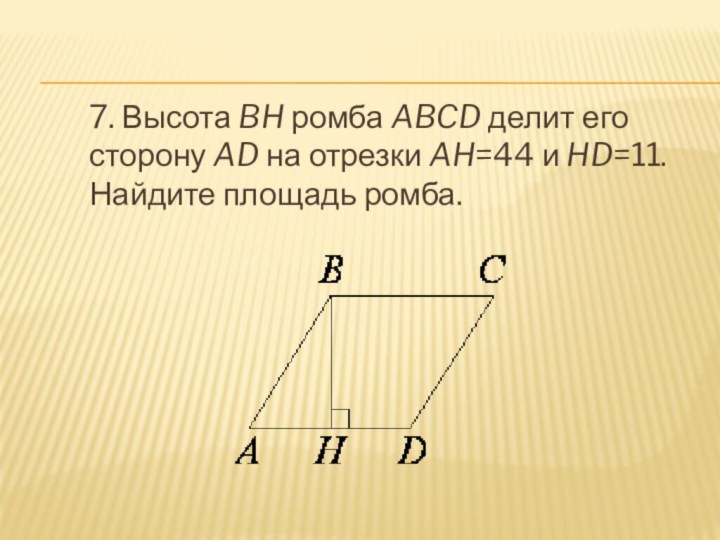
- 8. 7. Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
- 9. 8. Найдите площадь треугольника, изображённого на рисунке.
- 10. 9. Найдите площадь треугольника, изображённого на рисунке.
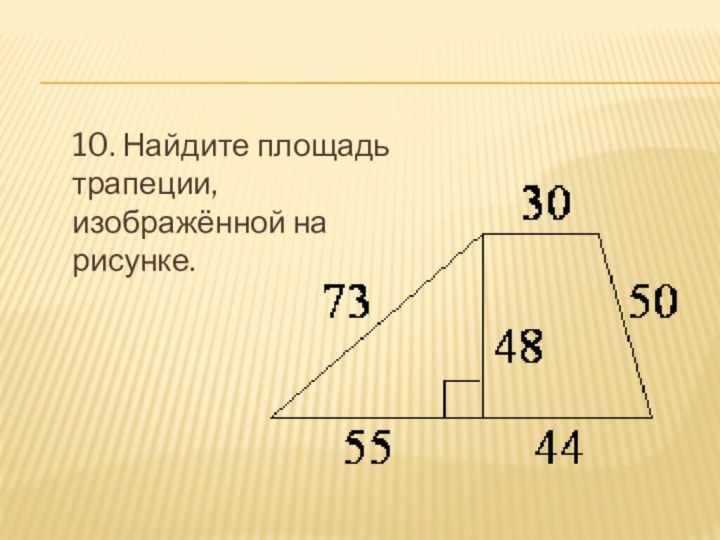
- 11. 10. Найдите площадь трапеции, изображённой на рисунке.
- 12. 11. На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.
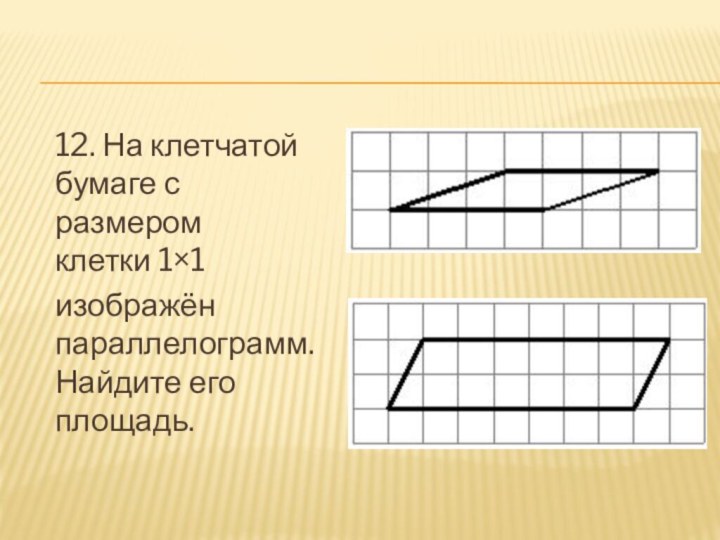
- 13. 12. На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
- 14. 13. В равнобедренной трапеции основания равны 2
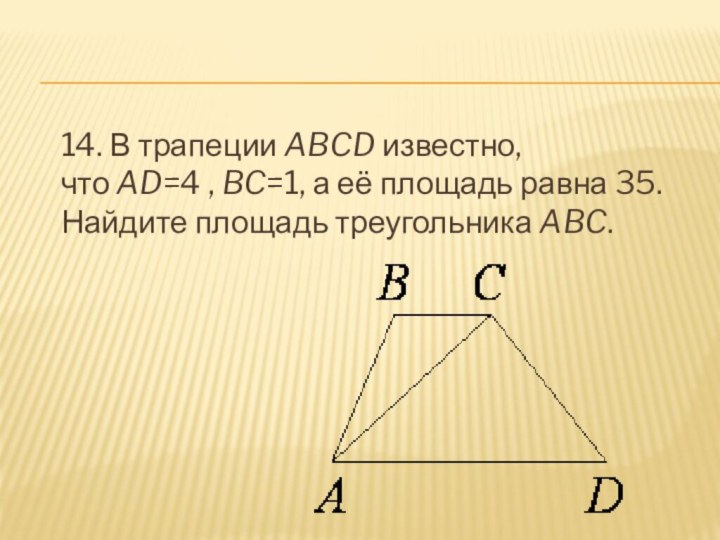
- 15. 14. В трапеции ABCD известно, что AD=4 , BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
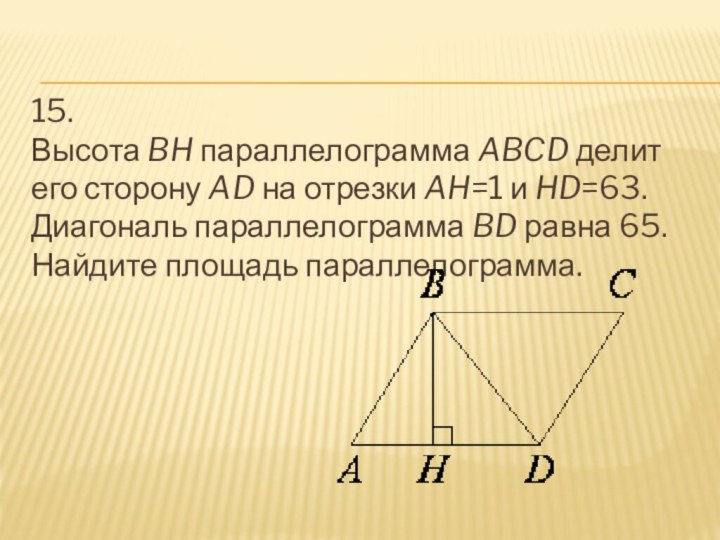
- 16. 15. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
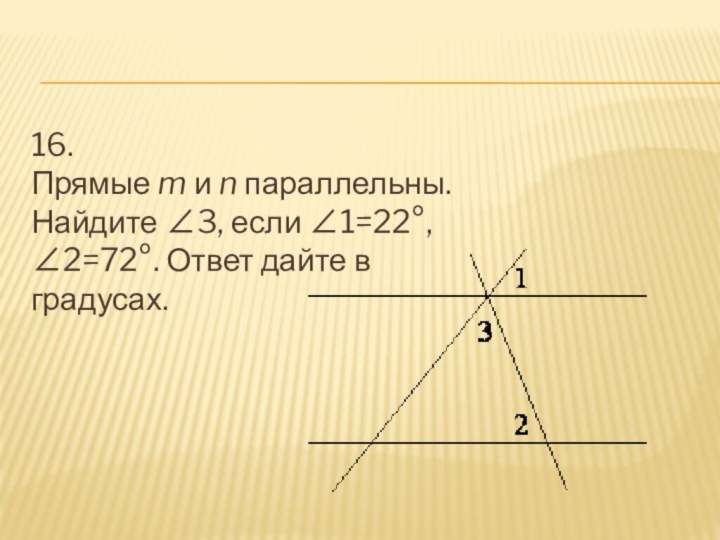
- 17. 16. Прямые m и n параллельны. Найдите ∠3, если ∠1=22°, ∠2=72°. Ответ дайте в градусах.
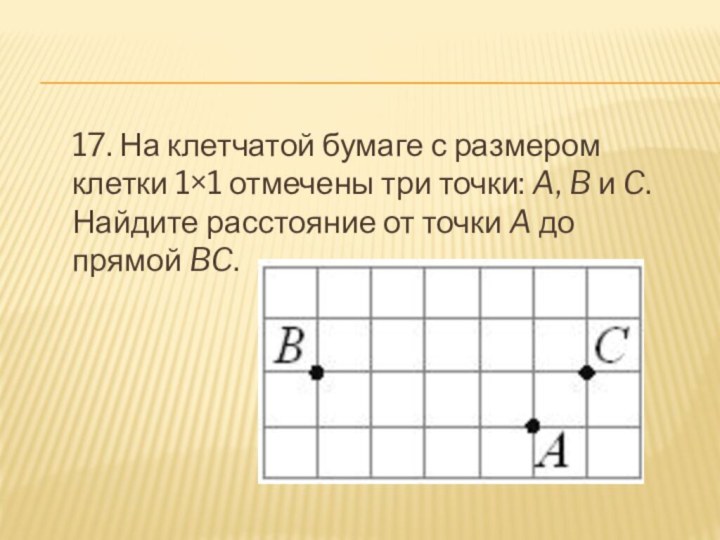
- 18. 17. На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.
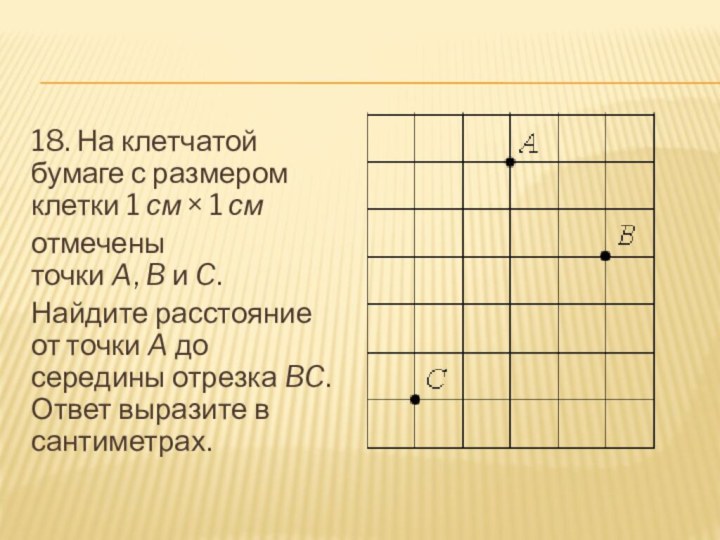
- 19. 18. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены
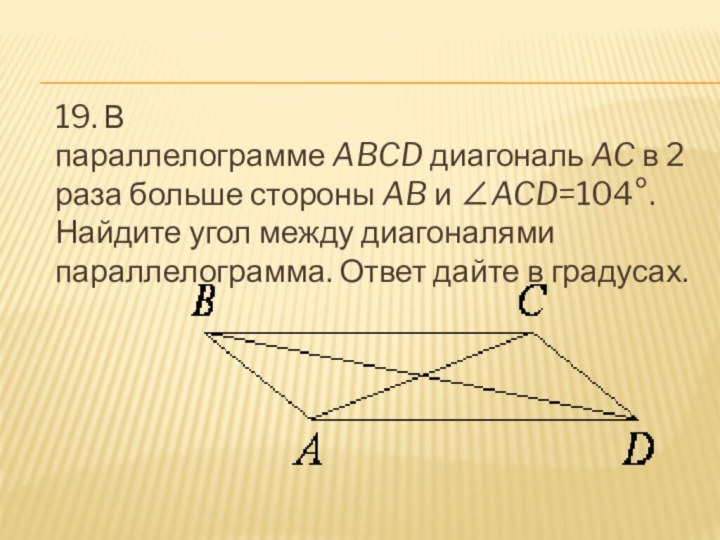
- 20. 19. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
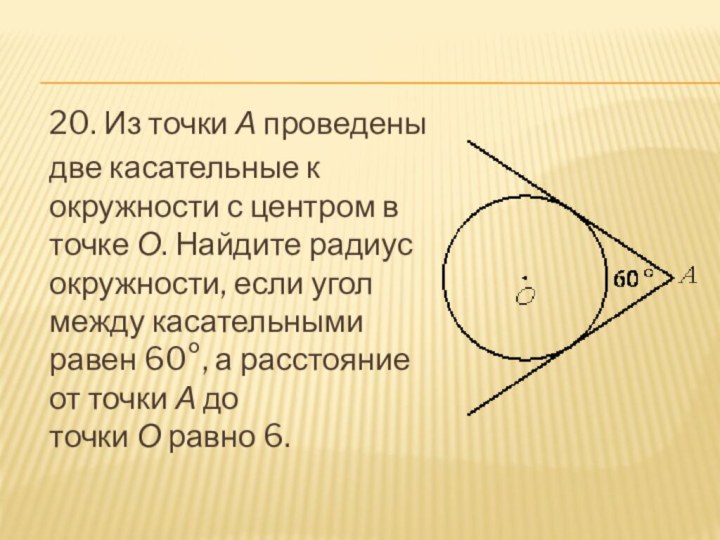
- 21. 20. Из точки А проведены две касательные к окружности
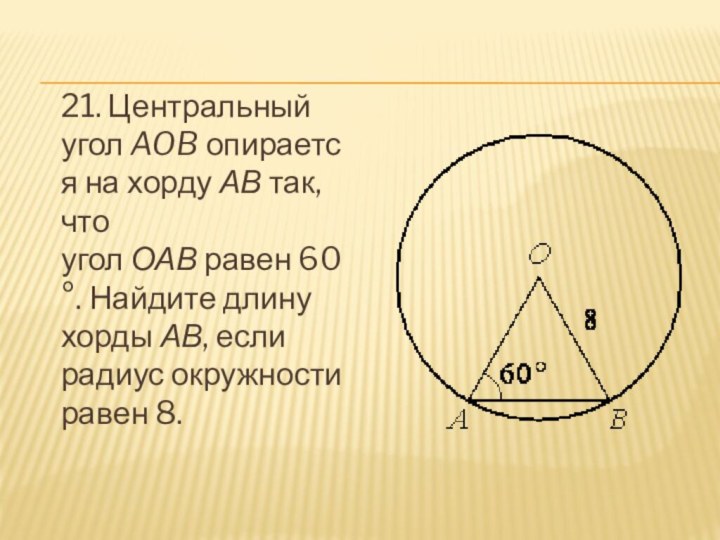
- 22. 21. Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 8.
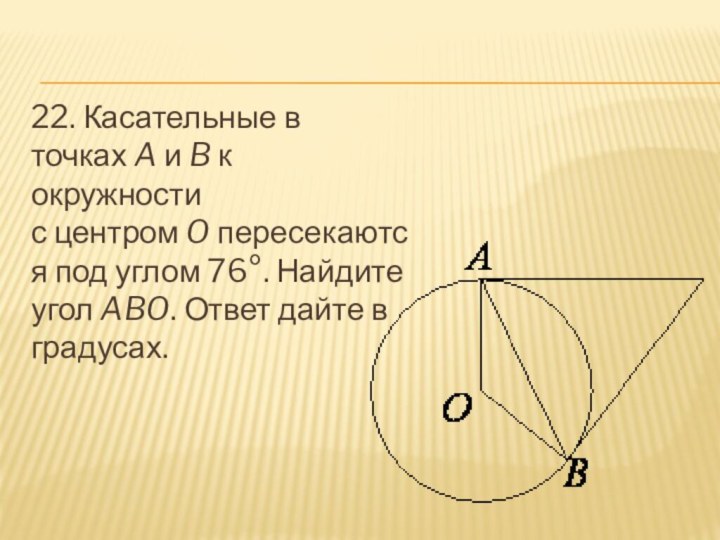
- 23. 22. Касательные в точках A и B к окружности с центром O пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
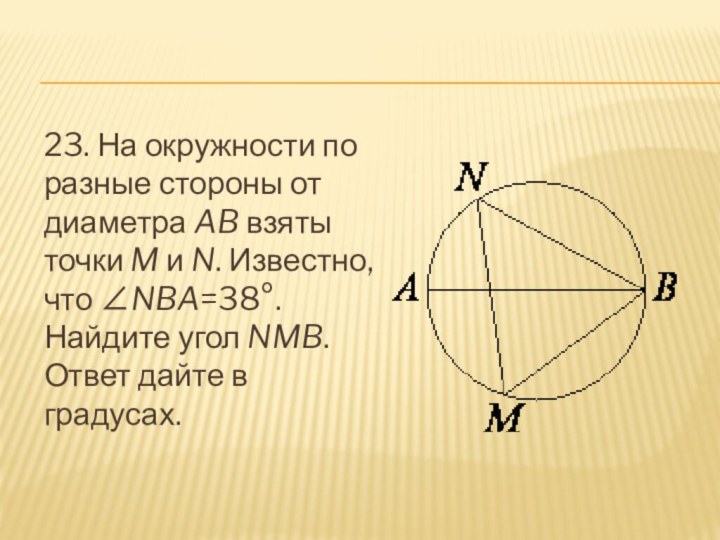
- 24. 23. На окружности по разные стороны от
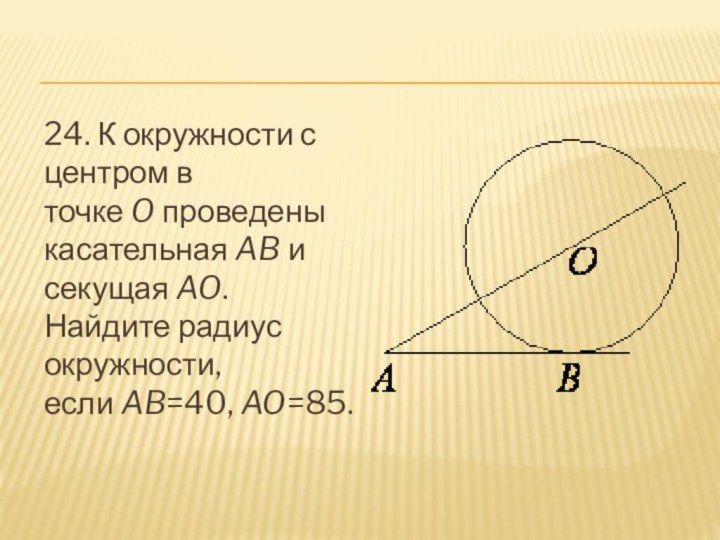
- 25. 24. К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
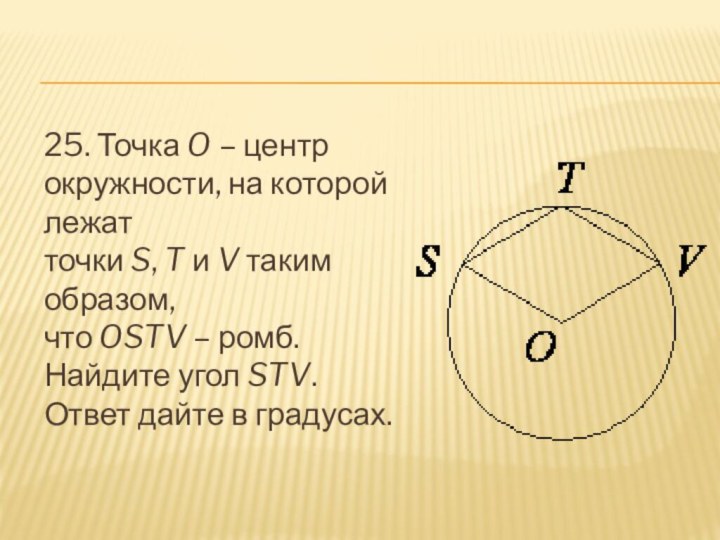
- 26. 25. Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол STV. Ответ дайте в градусах.
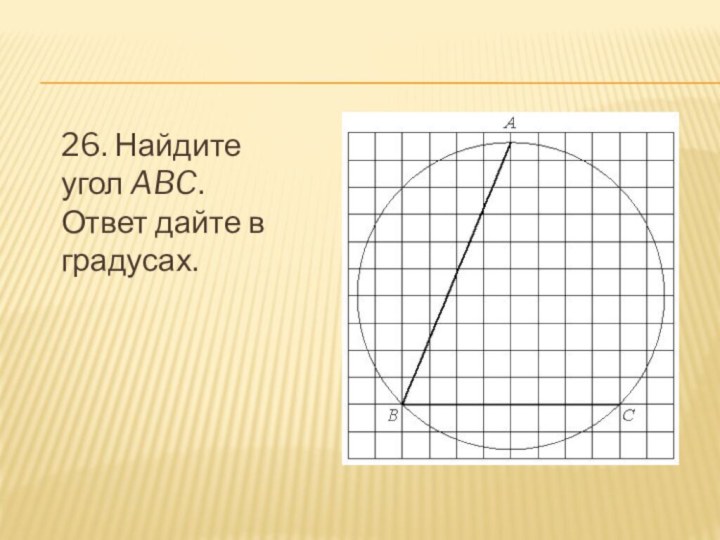
- 27. 26. Найдите угол ABC. Ответ дайте в градусах.
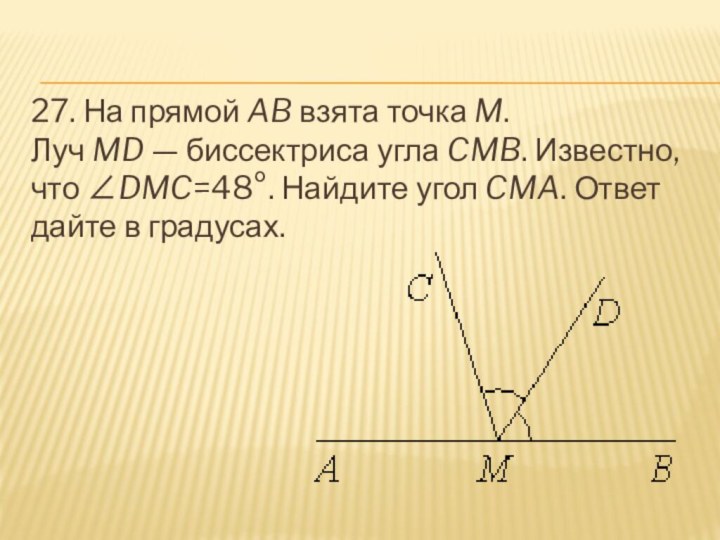
- 28. 27. На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC=48°. Найдите угол CMA. Ответ дайте в градусах.
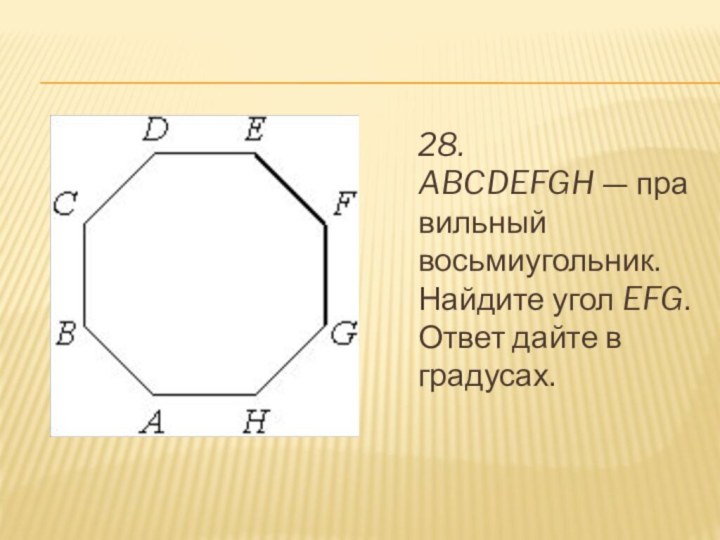
- 29. 28. ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
- 30. 29. Вершины треугольника делят описанную около него
- 31. 30. Пол комнаты, имеющей форму прямоугольника со
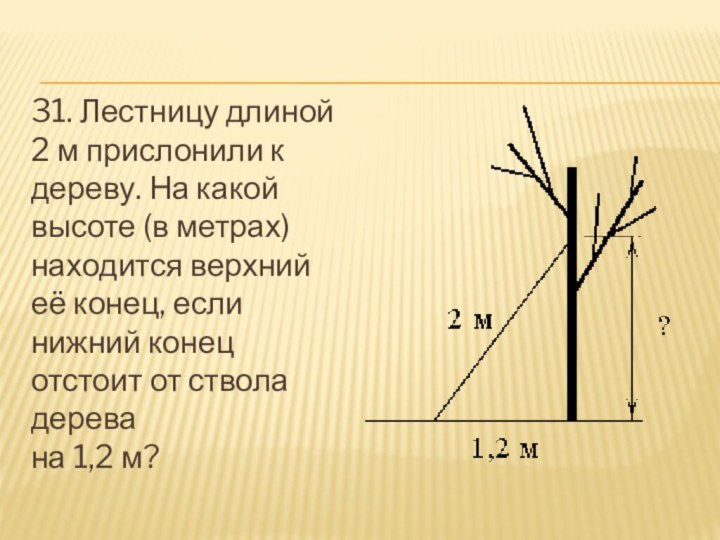
- 32. 31. Лестницу длиной 2 м прислонили к дереву.
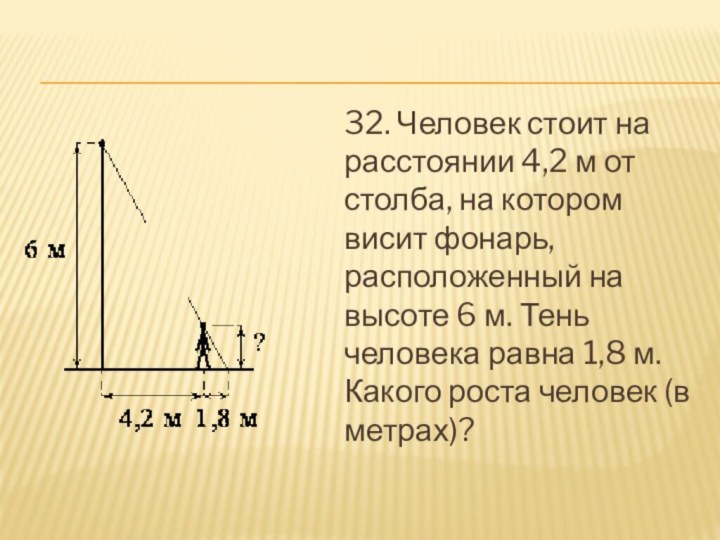
- 33. 32. Человек стоит на расстоянии 4,2 м
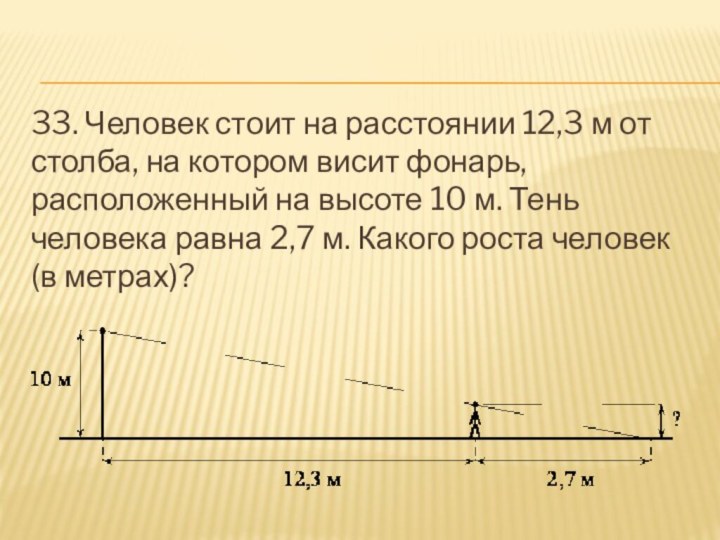
- 34. 33. Человек стоит на расстоянии 12,3 м
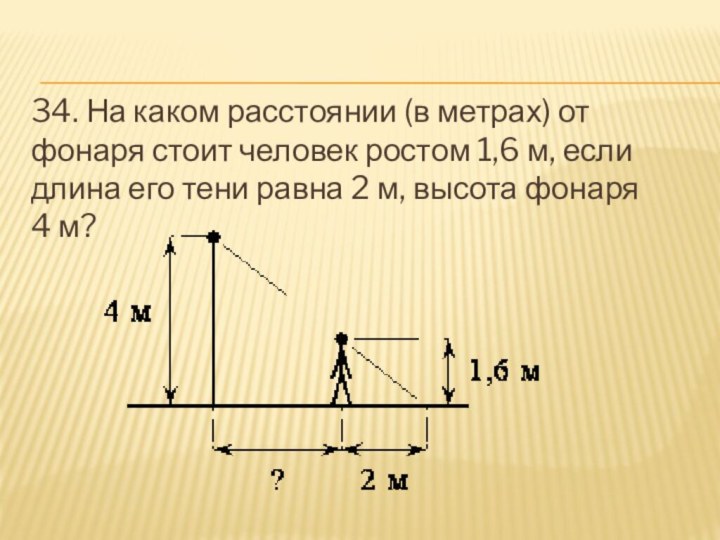
- 35. 34. На каком расстоянии (в метрах) от
- 36. 35. На рисунке изображён колодец с «журавлём».
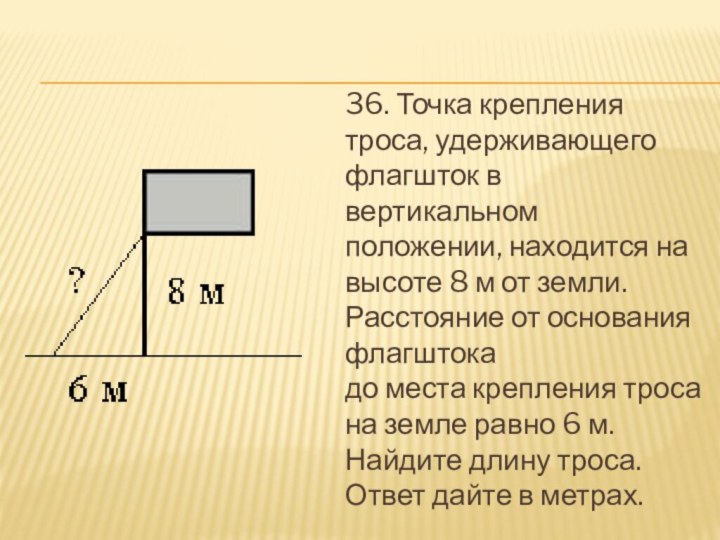
- 37. 36. Точка крепления троса, удерживающего флагшток в
- 38. Скачать презентацию
- 39. Похожие презентации
В треугольнике ABC известно, что AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.












Слайд 3
2. Какое из следующих утверждений верно?
1) Площадь квадрата
равна произведению двух его смежных сторон.
2) Диагональ трапеции делит
её на два равных треугольника.3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Слайд 4
3. Какое из следующих утверждений верно?
1)Все углы ромба
равны.
2)Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника,
то такие четырёхугольники равны.3)Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.