Слайд 2
СОДЕРЖАНИЕ:
Введение
Математика в рекламных стратегиях
2.1Тенденциозное
использование пропорций
2.2Вероятность
2.3 Как
математика помогает достичь совершенства
3. Математика в дизайне
3.1 Дух геометрии
3.2 Почему пазлы из 2000 элементов не содержат ровно 2000 элементов
4.Заключение
5. Используемая литература
Слайд 3
1.Введение
Математика всегда была и будет актуальной. Но давайте
же посмотрим, как математика используется в областях, которые сегодня
являются синонимом творчества вне рамок мира искусства, а именно в дизайне и рекламе.
Нет никаких сомнений относительно того, какую роль играла и продолжает играть геометрия в дизайне. Она неизбежно применяется при создании чего-то материального и осязаемого. С начала XX века чисто геометрические фигуры используются в дизайне самых разных товаров, особенно в дизайне мебели и упаковки. Дизайнеры, обладающие эстетическим вкусом, стремящиеся к абстракции и экономии форм, с помощью геометрических фигур делают свои работы более элегантными.
Слайд 5
Используется математика и в мире рекламы. Реклама в

потоке информации занимает поистине царское место при всей многообразности
и разнонаправленности современного информационного пространства. Поэтому в последние десятилетия растущий интерес к науке вдохновил авторов рекламных кампаний на использование различных математических инструментов, чтобы повысить доверие к рекламируемому товару. Графики, формулы, геометрические фигуры, символы, числа и расчёты стали всё чаще встречаться во всех средствах массовой информации, как печатных, так и аудиовизуальных.
Математика играет важную роль в дизайне и рекламе по двум причинам. С одной стороны, тот факт, что и дизайнеры, и специалисты по рекламе грамотно используют математические идеи, расширяет область применения этих идей. С другой стороны, когда математические понятия появляются в контекстах, не связанных с миром науки и технологий, они помогают по-новому понять знакомые нам идеи, делая их ещё более доступными.
Можно привести множество примеров применения математических идей в сфере дизайна или рекламы. Проанализируем некоторые из них.
Слайд 6
2. Математика в рекламных стратегиях
Непрерывная борьба за аудиторию
приводит к тому, что теле- и радиокомпании в свей
рекламе преувеличивают свои достижения и преуменьшают результаты конкурентов. Типичным примером является демонстрация графиков для того, чтобы сделать рекламу убедительнее. Чтобы подчеркнуть преимущество телеканала А над телеканалом В по охвату территории, обычно используются графики, подобные следующему:
2.1 Тенденциозное использование
пропорций
Слайд 8
Допустим, что приведённые на графике данные верны, и
телеканал A действительно популярнее телеканала B. Тем не менее
разница в размерах между столбцами диаграммы значительно преувеличивает это преимущество. Прямоугольник, обозначающий аудиторию телеканала A, намного больше, чем прямоугольник, обозначающий аудиторию канала B:
A: 29,6 – 27,5 = 2,1
B: 28,8 – 27,5 = 1,3 A/B= 2,1/1,3 = 1,615.
В действительности разница между аудиториями каналов составляет восемь десятых процента, поэтому высота одного прямоугольника должны быть менее чем на 2,8% больше высоты другого. Корректнее было бы изобразить прямоугольники в всю длину:
Слайд 10
Похожая проблема связана и с графиками, иллюстрирующими колебания
курсов валют. Изменение курса валют в течение недели может
показаться незначительным или огромным в зависимости от выбранного масштаба вертикальной оси графика:
Слайд 12
Стремление проиллюстрировать на графиках отношение величин или их
разницу очень часто встречаются в рекламе, но, к сожалению,
результат оказывается прямо противоположным: точность графиков является мнимой. Числа и графики обладают строгостью, присущей математике, но только при объективном использовании.
Слайд 13
2.2 Вероятность
Несколько лет назад одной рекламе одной телефонной
кампании прозвучала фраза: «Вероятность того, что сын вашего начальника
и вы – это один и тот же человек, равна 0,00000000001%».
В математике вероятность – это численная характеристика возможности возникновения какого-либо события. Классическое определение вероятности звучит как отношение числа благоприятных исходов к общему числу возможных исходов. Например, вероятность того, что при броске шестигранного кубика выпадет число очков х, меньшее 3, равна 2/6, так как число благоприятных исходов равно 2 (выпадет одно либо два очка), общее число исходов – 6:
P(х 3) = 2/6 = 1/3 = 0,333…
Слайд 14
Чтобы рассчитать вероятность того, что некий человек –
сын вашего начальника, нужно найти отношение числа благоприятных исходов
к общему числу возможных исходов. Так как у любого человека может быть только один отец, число благоприятных исходов равно единице. Чтобы определить число возможных исходов, нужно узнать, сколько всего начальников в мире, что практически невозможно. Из общего числа жителей Земли, превышающего шесть миллиардов человек, нужно исключить женщин (речь идёт о начальнике, а не о начальнице), бездетных, безработных и тех, кто не занимает руководящую должность. Тогда число возможных исходов будет меньше половины от шести миллиардов. Таким образом, вероятность будет равна:
P = 1 / 3х 10 = 3,33х 10
Вероятность, указанная в рекламном слогане, равна:
Q = 0,00000000001 / 100 = 10
Слайд 15
Это предполагает существование 10 начальников и численность населения
Земли, равную 2х10 человек, а это в 600 раз
больше реального населения Земли:
P/Q = 3,33х10 / 2х10 = 600
Нам неизвестно, почему автор рекламного слогана выбрал именно число 0,00000000001%, однако ему, несомненно, удалось показать, что ни один человек на планете не является сыном своего начальника. Чем больше нулей после запятой в записи десятичной дроби, тем меньше значение этой дроби. Если приписать у этому числу знак %, оно уменьшится ещё в сто раз.
Перед нами – пример творчества, в котором невозможность события подчёркивается с помощью очень малой величины. Хотя 0% описывает вероятность абсолютно невозможного события, визуальный эффект от числа 0,00000000001% выше, поэтому автор его и использовал.
-10
-13
Слайд 16
2.3 Как математика помогает достичь совершенства
Некоторое время назад
один из производителей вина запустил рекламную кампанию, смысл которой
сводился к тому, что совершенство его продукции обусловлено сочетанием математики, природы и мастерства. В рекламном ролике показывался длиннейший ряд математических формул, большинство из которых не несли особого смысла, а многие цифры и буквы в них были заменены изображениями природы или фотографиями мастеров-виноделов. Ряд формул заканчивался знаком равенства, по другую сторону которого была изображена бутылка вина. Рядом с бутылкой располагался слоган: «Кто сделал его совершенным?».
Замысел автора рекламы заключался в том, чтобы с помощью математических инструментов показать, сколь длительным и скрупулёзным является процесс изготовления вина, ведь именно слова «длительность» и «скрупулёзность» описывают большую часть математической деятельности.
Слайд 17
3. Математика в дизайне
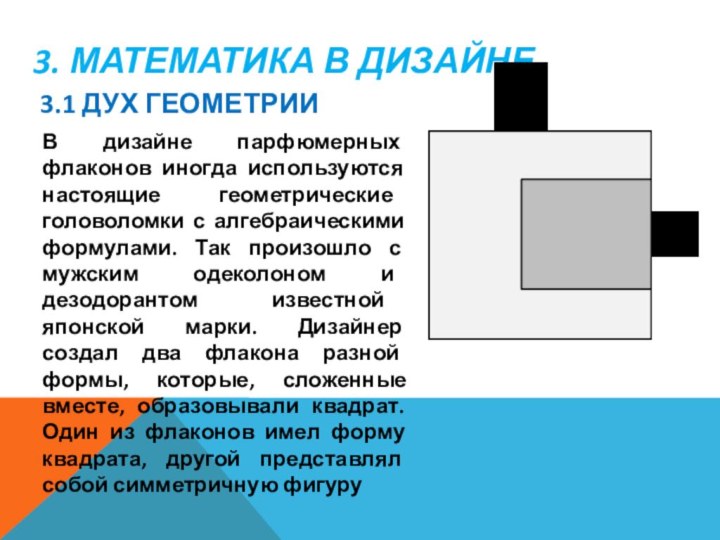
В дизайне парфюмерных флаконов иногда
используются настоящие геометрические головоломки с алгебраическими формулами. Так произошло
с мужским одеколоном и дезодорантом известной японской марки. Дизайнер создал два флакона разной формы, которые, сложенные вместе, образовывали квадрат. Один из флаконов имел форму квадрата, другой представлял собой симметричную фигуру
3.1 Дух геометрии
Слайд 18
Вместимость большого флакона равнялась 75 мл, малого –
50 мл. В рекламе основной упор делался на суммарном
объёме флаконов и их особой форме:
Z
Z
X
X
Слайд 19
Сможете ли вы определить реальные размеры флаконов? Объём
меньшего равен 50 мл, большего - 75 мл. Суммарный
объём флаконов 125 мл. Так как флаконы идеально укладываются друг в друга, их толщина одинакова, следовательно, их объёмы пропорциональны площадям видимых поверхностей. Учитывая, что 1 мл воды эквивалентен 1 см, можно вполне ооснованно считать, что сторона Х малого флакона и сторона Z большого флакона соответственно равны:
50 = X , следовательно, х = корень из 50 = 7,1 см;
125 = Z , следовательно, Z = корень из 125 = 11,2 см.
Слайд 20
3.2 Почему пазлы из 2000 элементов не содержат
ровно 2000 элементов
Не всегда можно создать предметы точно такой
формы или из точно такого числа элементов, как этого хочется их автору. Многие из вас наверняка собирали головоломки-пазлы, но немногие подсчитывали точное число их элементов. Некоторые могут возразить, что подобный подсчёт не нужен, так ка число элементов всегда указано на коробке: 500, 1000, 2000, 3000, 5000, 8000. Однако изготовители головоломок обманывают нас, или, по меньшей мере, не говорят всей правды.
Пазлы из 500 элементов действительно содержат 500 элементов, но пазлы из 2000 элементов не содержат 2000 элементов, и чтобы убедиться в этом, не требуется подсчитывать их все. Все пазлы образуют форму прямоугольника, их элементы имеют различную форму, однако вырезаются из прямоугольного основания, в котором проделываются выступы и выемки.
Слайд 21
При изготовлении пазла из 2000 элементов нужно найти
два целых числа, обозначающих число элементов на каждой стороне
прямоугольника, произведение которых будет равно 2000. Так как 2000 = 2х2х2х2х5х5х5, возможны следующие варианты:
1х2000 = 2х1000 = 4х500 = 8х250 = 10х200 = 16х125 = 20х100 = 25х80 = 40х50.
Соотношение ширины и высоты собранного пазла должно быть гармоничным и приближаться к соотношению сторон листа стандартного формата А4, то есть примерно равно 1,4. Однако прямоугольники, длины сторон которых являются делителями числа 2000, будут либо слишком вытянутыми, либо слишком «квадратными»:
50/40 = 1,25 80/25 = 3,2
Поэтому вместо 2000 используется 1998 элементов: разложив 1998 на простые множители, мы увидим, что два его делителя описывают прямоугольник, соотношение сторон которого очень близко к желаемому:
1998 = 2х3х3х3х37, следовательно, (2х3х3х3)/37 = 1,46
Это интересный пример того, как разложение натурального числа на простые множители определяет дизайн предмета.
Слайд 22
4. Заключение
Каковы особенности математического творчества? Творить математику означает,
прежде всего, иметь необходимые идеи, чтобы прокладывать пути к
новым формулам, теоремам и методам, которые постепенно позволят понять интересующие нас события и явления.
И чтобы обычный человек смог понять суть математического творчества, ему стоит применить математические методы и понятия для анализа различных событий повседневной жизни, явлений из сферы искусства, литературы или рабочих ситуаций. Взгляд в зеркало или в сторону горизонта побуждает творить формулы и определять отношения, помогающие лучше понять мир. Ни одну из этих формул нельзя считать результатом открытия – она не находилась по другую сторону зеркала и не погребена была в песке. Эти формулы родились благодаря нашему воображению, способному моделировать реальность в виде множества геометрических фигур. Без нас не было ни формул, ни горизонта.
Слайд 23
Творить означает создавать что-то, чего раньше не существовало,
будь то объект, процедура или понятие. Творить математику, по
сути, означает решать задачи, поэтому мы делаем первый шаг к творчеству, когда задаёмся вопросом, на который может ответить математика. Этот вопрос может родиться из другой математической задачи, теоремы или какого-то явления повседневной жизни. Погрузившись в суть вопроса, нужно внимательно изучить его, и в этом очень важную роль может сыграть социальное и культурное взаимодействие. Когда мы обмениваемся с другими людьми нашими идеями и рассказываем о неудачах, это помогает осветить «тёмную комнату», в которую мы попали.
Технологии могут оказать нам огромную помощь и стать источником вдохновения, поскольку позволяют реализовать самые немыслимые плоды нашего воображения.
Слайд 24
И я полагаю, что творить математику может любой
и что математика намного более демократична, чем это кажется
с учётом человеческой истории и традиций в сфере образования. В чём же состоит метод, который поможет нам стать творцами и создать новую математику? На основании всего ранее изложенного можно заключить, что этот метод состоит в том, чтобы:
- посмотреть на ситуацию с точки зрения математики;
- сформулировать задачу на языке математики;
- не стесняясь, использовать эксперимент, интуицию, аналогии, логику, технологии и социокультурные достижения, например, труды экспертов и работы других авторов.
Иными словами, нужно каждый день хотя бы несколько мгновений жить математически.
И дорогие слушатели, успехов вам в творчестве!