- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Сечения параллелепипеда
Содержание
- 2. Взаимное расположение плоскости и многогранникаbcdaa. Нет точек
- 3. Определение Если пересечением многогранника и плоскости является многоугольник, то он называется сечением многогранника указанной плоскостью
- 4. Особенность 1. Все стороны многоугольника-сечения лежат в
- 5. Особенность 2. Каждую грань многогранника сечение может пересекать не более, чем по одной прямой.
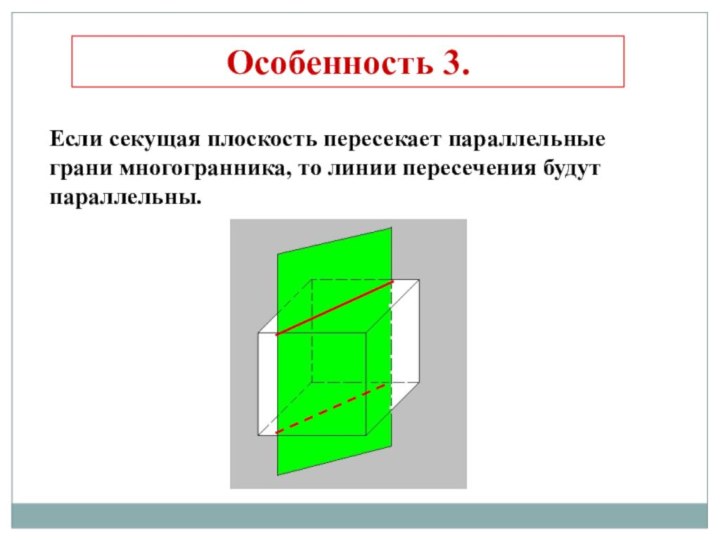
- 6. Если секущая плоскость пересекает параллельные грани многогранника, то линии пересечения будут параллельны.Особенность 3.
- 7. 3. Если секущая плоскость пересекает параллельные грани
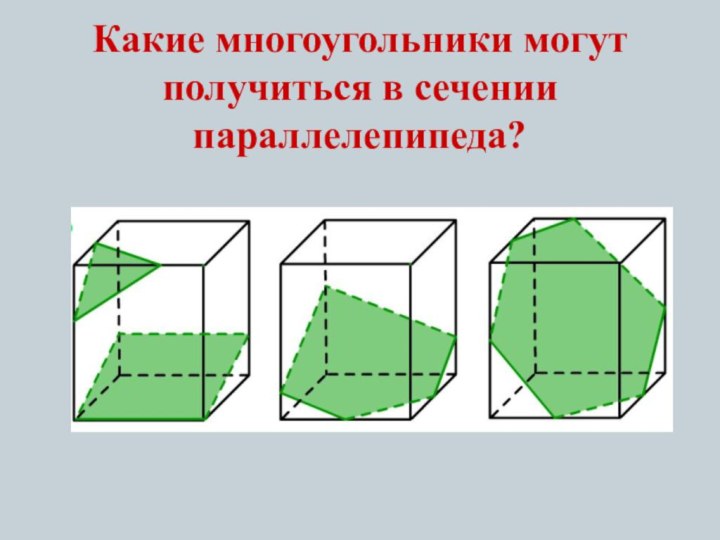
- 9. Какие многоугольники могут получиться в сечении параллелепипеда?
- 10. MN1)ß PA1D1=PM;2)ß DD1C1=MN;3)ß PDC=PN;PMN – искомое сечение
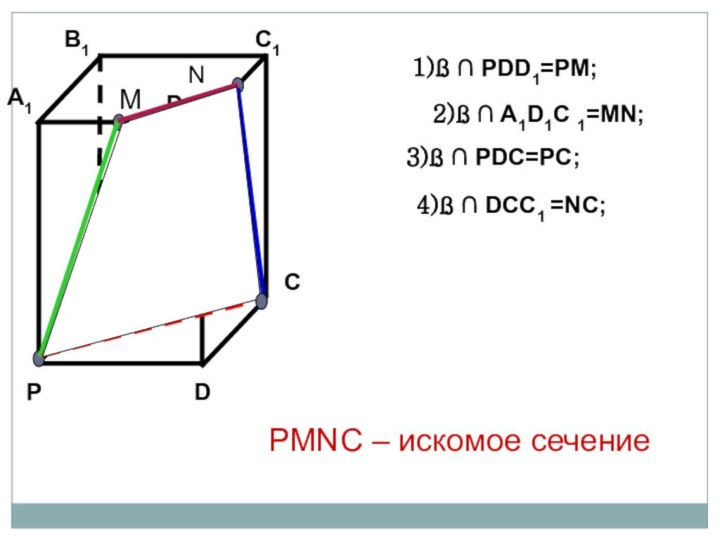
- 11. MN1)ß PDD1=PM;2)ß A1D1C 1=MN;3)ß PDC=PC;4)ß DCC1 =NC;PMNC – искомое сечение
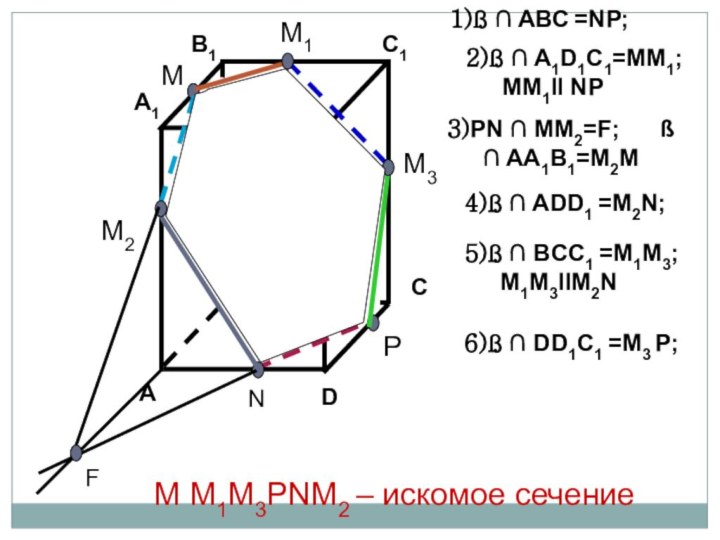
- 12. PMNDA1B1C1D1BCAM1P11)ß BB1C1 =NP;2)ß ADD1=MM1; ,
- 13. Скачать презентацию
- 14. Похожие презентации
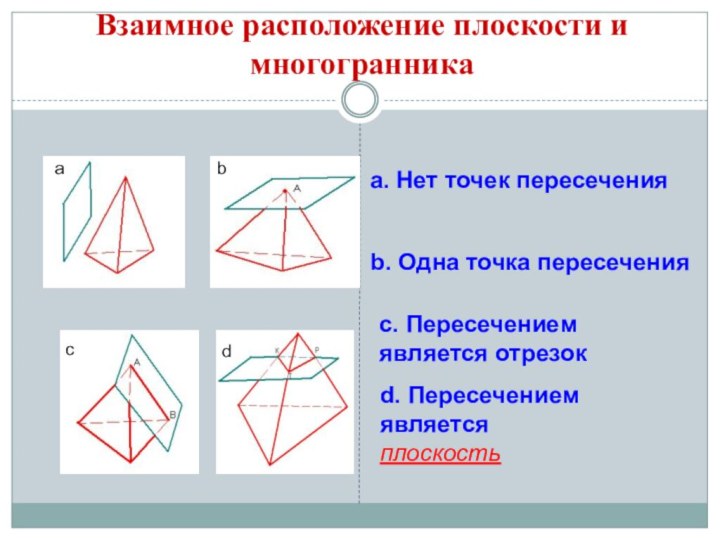
Взаимное расположение плоскости и многогранникаbcdaa. Нет точек пересеченияb. Одна точка пересеченияc. Пересечением является отрезокd. Пересечением является плоскость








Слайд 2
Взаимное расположение плоскости и многогранника
b
c
d
a
a. Нет точек пересечения
b.
Одна точка пересечения
Слайд 3
Определение
Если пересечением многогранника и плоскости является многоугольник, то
он называется сечением многогранника указанной плоскостью
Слайд 4
Особенность 1.
Все стороны многоугольника-сечения лежат в плоскостях
граней многогранника.
Никакая из сторон сечения не может проходить внутри
многогранника!
Слайд 5
Особенность 2.
Каждую грань многогранника сечение может пересекать
не более, чем по одной прямой.
Слайд 6 Если секущая плоскость пересекает параллельные грани многогранника, то
линии пересечения будут параллельны.
Особенность 3.
Слайд 7 3. Если секущая плоскость пересекает параллельные грани многогранника,
то линии пересечения будут параллельны.
1. Никакая из сторон сечения
не может проходить внутри многогранника2. Каждая грань многогранника содержит не более одной стороны сечения.
!
!
!
Слайд 12
P
M
N
D
A1
B1
C1
D1
B
C
A
M1
P1
1)ß BB1C1 =NP;
2)ß ADD1=MM1; , MM1ll
NP
3)ß AA1B1=M1N;
4)ß DD1C1 =PP1; PP1ll M1N
5)ß
ADC =MP1;M1NPP1 M – искомое сечение