Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Подобные треугольники

Содержание

Оглавление Определение подобных треугольников Признаки подобия треугольников Применение подобия к доказательству теорем и задач Соотнашение между сторонами и углами прямоугольного треугольника
Подобные треугольники Оглавление Определение подобных треугольников Признаки подобия треугольников Применение подобия к доказательству теорем 1.1. Пропорциональные отрезки.1.2. Определение подобных треугольников1.3. Отношение площадей подобных треугольников.1.4. Свойства подобия.Определение подобных треугольников 1.1 Пропорциональные отрезки.Отношением отрезков AB и CD называется отношение их длин, т. 1.2. Определение подобных треугольников. В повседневной жизни встречаются предметы одинаковой формы, но разных 1.2. Определение подобных треугольников.ПОДОБИЕ, геометрическое понятие, характеризующее наличие одинаковой формы у геометрических 1.2. Определение подобных треугольников.Задача№1.Пусть у двух треугольников ABC и A1B1C1 соответственно равны: 1.2. Определение подобных треугольников.АB C А1B1C1AB и A1B1, BC и B1C1, CA и C1A1- сходственные стороны 1.2. Определение подобных треугольников.Определение. Два треугольника называются подобными, если их углы соответственно 1.2. Определение подобных треугольников.Подобие треугольников ABC и A1B1C1 обозначается так : Нажмите сюда и увидите подобные треугольники 1.3. Отношение площадей подобных треугольников.Теорема. Отношение площадей двух подобных треугольников равно квадрату 1.3. Отношение площадей подобных треугольников. По формулам имеем: поэтому Теорема доказана. Свойства подобия.Задача №2. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные Свойства подобия.С другой стороны, эти же треугольники имеют по равному углу( Признаки подобия треугольников Первый признак Второй признак Третий признак Теорема: Если два угла одного треугольника соответственно равны двум углам другого, то Доказательство:По теореме о сумме углов: С = 1800 - А Теорема. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и АВС2 А1В1С1(по первому признаку) ,значит Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие Доказательство:Рассмотрим АВС2, у которого Применение подобия к доказательству теорем и задач Средняя линия треугольника Медианы в Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон. Теорема: Дано: АВСМN – средняя линияДоказать:МN //АС и MN=1/2ACСредняя линия треугольника Доказательство: Меридианы треугольника пересекаются в одной точке, которая делит каждую меридиану в отношении Доказательство:А1В1 – средняя линия, и А1В1//АВ, поэтому Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два Доказательство: АВС АСН(по двум углам: А- как общий Отрезок ХY называется средним пропорциональным (или средним геометрическим) между отрезками АВ и СД, еслиСреднее пропорциональное Дано: АВС – прямоугольныйСН – высотаДоказать:Высота прямоугольного треугольника, проведенная из вершины Дано: АВС – прямоугольныйСН – высотаДоказать:Катет прямоугольного треугольника есть среднее пропорциональное Соотнашение между сторонами и углами прямоугольного треугольника Синус Косинус Тангенс Значение синуса, Синус Синус острого угла прямоугольного треугольника – это отношение противолежащего катета к гипотенузе. АСВ АВСКосинус Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе. АВСТангенс Тангенс острого угла прямоугольного треугольника – это отношение противолежащего катета к прилежащему катету. АВСКотангенс Тангенс острого угла прямоугольного треугольника – это отношение прилежащего катета к противолежащему катету. АВСОсновные тригонометрические тождества. 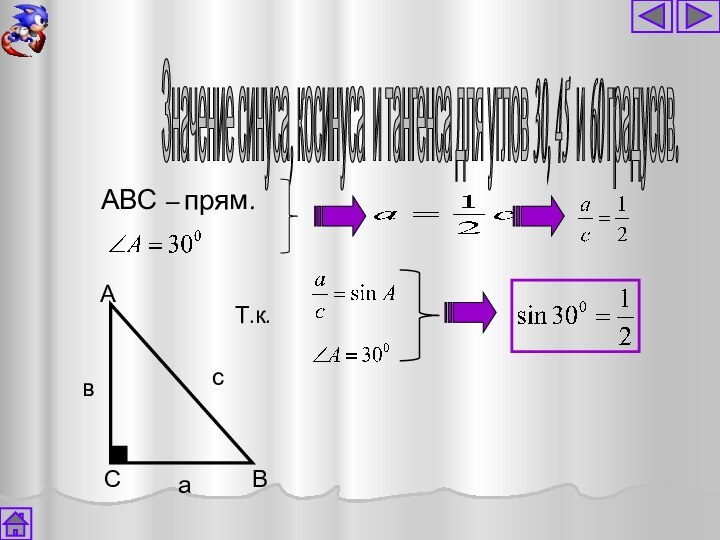АВСЗначение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов. АВС – прям.Т.к.вса АВСЗначение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов. АВСЗначение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов. вса АВСЗначение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов. вса Конец
Слайды презентации

Слайд 2 Оглавление
Определение подобных треугольников
Признаки подобия треугольников
Применение

Оглавление Определение подобных треугольников Признаки подобия треугольников Применение подобия к доказательству

подобия к доказательству теорем и задач
Соотнашение между сторонами

и углами прямоугольного треугольника

Слайд 3 1.1. Пропорциональные отрезки.
1.2. Определение подобных треугольников
1.3. Отношение площадей

1.1. Пропорциональные отрезки.1.2. Определение подобных треугольников1.3. Отношение площадей подобных треугольников.1.4. Свойства подобия.Определение подобных треугольников

подобных треугольников.
1.4. Свойства подобия.
Определение подобных треугольников



Слайд 4 1.1 Пропорциональные отрезки.
Отношением отрезков AB и CD называется

1.1 Пропорциональные отрезки.Отношением отрезков AB и CD называется отношение их длин,

отношение их длин, т. е.



Говорят, что отрезки AB

и CD пропорциональны отрезкам A1B1 и C1D1, если



ПРИМЕР №1.
Отрезки AB и CD, длины которых равны 2 см и 1см, пропорциональны отрезкам A1B1 и C1D1,отрезки которых равны 3см и 1,5см. В самом деле,







Слайд 5 1.2. Определение подобных треугольников.
В повседневной жизни встречаются предметы

1.2. Определение подобных треугольников. В повседневной жизни встречаются предметы одинаковой формы, но

одинаковой формы, но разных размеров, например футбольный и теннисный

мячи, круглая тарелка и большое круглое блюдо. В геометрии фигуры одинаковой формы принято называть подобными. Так, подобными являются любые два квадрата, любые два круга. Введем понятие подобных треугольников.




Слайд 6 1.2. Определение подобных треугольников.
ПОДОБИЕ, геометрическое понятие, характеризующее наличие

1.2. Определение подобных треугольников.ПОДОБИЕ, геометрическое понятие, характеризующее наличие одинаковой формы у

одинаковой формы у геометрических фигур, независимо от их размеров.

Две фигуры F1 и F2 называются подобными, если между их точками можно установить взаимно однозначное соответствие, при котором отношение расстояний между любыми парами соответствующих точек фигур F1 и F2 равно одной и той же постоянной k, называемой коэффициентом подобия. Углы между соответствующими линиями подобных фигур равны.

Подобные фигуры F1 и F2.




Слайд 7 1.2. Определение подобных треугольников.
Задача№1.
Пусть у двух треугольников ABC

1.2. Определение подобных треугольников.Задача№1.Пусть у двух треугольников ABC и A1B1C1 соответственно

и A1B1C1 соответственно равны: A=

A1, B= B1, C= C1. В этом случае стороны AB и A1B1, BC и B1C1, CA и C1A1 называются сходными.




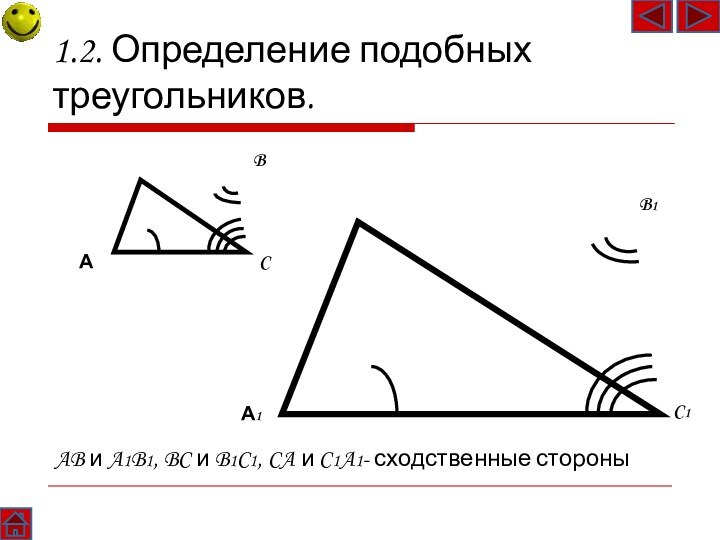
Слайд 8 1.2. Определение подобных треугольников.



А
B
C
А1
B1
C1
AB и A1B1,

1.2. Определение подобных треугольников.АB C А1B1C1AB и A1B1, BC и B1C1, CA и C1A1- сходственные стороны

BC и B1C1, CA и C1A1- сходственные стороны


















Слайд 9 1.2. Определение подобных треугольников.
Определение. Два треугольника называются подобными,

1.2. Определение подобных треугольников.Определение. Два треугольника называются подобными, если их углы

если их углы соответственно равны и стороны одного треугольника

пропорциональны сходственным сторонам другого треугольника.
Другими словами, два треугольника подобны, если их можно обозначить буквами ABC и A1B1C1 так, что A= A1, B= B1, C= C1,



Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.




Слайд 10 1.2. Определение подобных треугольников.

Подобие треугольников ABC и A1B1C1

1.2. Определение подобных треугольников.Подобие треугольников ABC и A1B1C1 обозначается так : Нажмите сюда и увидите подобные треугольники

обозначается так :






Нажмите сюда и увидите подобные треугольники



Слайд 11 1.3. Отношение площадей подобных треугольников.
Теорема. Отношение площадей двух

1.3. Отношение площадей подобных треугольников.Теорема. Отношение площадей двух подобных треугольников равно

подобных треугольников равно квадрату коэффициента подобия.
Доказательство. Пусть треугольники ABC

и A1B1C1 подобны и коэффициент подобия равен k. Обозначим буквами S и S1 площади этих треугольников. Так как
A= A1, то





Слайд 12 1.3. Отношение площадей подобных треугольников.
По формулам имеем:


поэтому


Теорема

1.3. Отношение площадей подобных треугольников. По формулам имеем: поэтому Теорема доказана.

доказана.




Слайд 13 Свойства подобия.
Задача №2.
Докажите, что биссектриса треугольника делит противоположную

Свойства подобия.Задача №2. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки,

сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Решение.
Пусть AD –

биссектриса треугольника ABC. Докажем, что


Треугольники ABD и ACD имеют общую высоту AH, поэтому



1

2

A

H

B

D

C




Слайд 14 Свойства подобия.
С другой стороны, эти же треугольники имеют

Свойства подобия.С другой стороны, эти же треугольники имеют по равному углу(

по равному углу( A= A1),

поэтому


Из двух равенств для отношений площадей получаем

, или

Что и требовалось доказать.




Слайд 15 Признаки подобия треугольников



Первый признак
Второй признак
Третий

Признаки подобия треугольников Первый признак Второй признак Третий признак

признак



Слайд 16 Теорема: Если два угла одного треугольника соответственно равны

Теорема: Если два угла одного треугольника соответственно равны двум углам другого,

двум углам другого, то такие треугольники подобны.
Первый признак

А= А1
В= В1


АВС А1В1С1








Слайд 17 Доказательство:
По теореме о сумме углов: С =

Доказательство:По теореме о сумме углов: С = 1800 - А -

1800 - А - В, а

С1 = 1800 - - А 1- В1 ,значит С= С1.
Так как А= А1 и С= С1, то и
От этого следует:
Получается, что сходственные стороны пропорциональны.

Дано: АВС и А1В1С1
А= А1
В= В1
Доказать: АВС А1В1С1

Первый признак













А

С

В

А1

В1

С1






Слайд 18 Теорема. Если две стороны одного треугольника пропорциональны двум

Теорема. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника

сторонам другого треугольника и углы, заключенные между этими сторонами,

равны, то такие треугольники подобны.

Второй признак


АВС А1В1С1







Слайд 19 АВС2

АВС2 А1В1С1(по первому признаку) ,значит

А1В1С1(по первому признаку) ,значит

, с другой стороны ,из этих равенств получается АС= =АС2. АВС= АВС2 -по двум сторонам и углу между ними (АВ-общая сторона, АС=АС2 и ,т.к. и
).Значит и , то

АВС А1В1С1

Дано: АВС и А1В1С1

Второй признак



Д-ть:




Доказательство:
Рассмотрим АВС2, у которого
и








Слайд 20 Теорема: Если три стороны одного треугольника пропорциональны трем

Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого, то

сторонам другого, то такие треугольники подобные.
Третий признак
АВС

А1В1С1







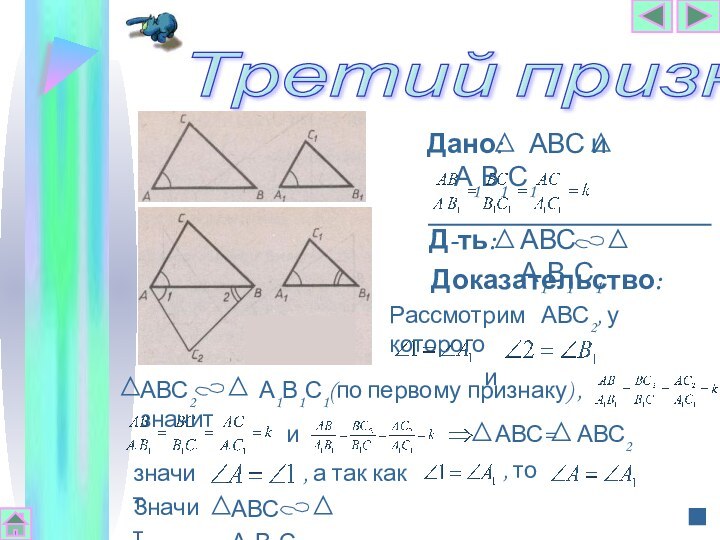
Слайд 21 Доказательство:
Рассмотрим АВС2, у которого

Доказательство:Рассмотрим АВС2, у которого и

и

.

Третий признак




Дано: АВС и А1В1С1

Д-ть:

АВС А1В1С1






АВС2 А1В1С1(по первому признаку) ,значит




и

АВС= АВС2



значит

, а так как

, то

Значит

АВС А1В1С1





Слайд 22 Применение подобия к доказательству теорем и задач
Средняя

Применение подобия к доказательству теорем и задач Средняя линия треугольника Медианы

линия треугольника
Медианы в треугольнике
Высота в треугольнике
Среднее

пропорциональное

Следствие 1

Следствие 2




Слайд 23 Средняя линия треугольника – это отрезок, соединяющий середины

Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.

двух его сторон.
Теорема: Средняя линия треугольника параллельна одной

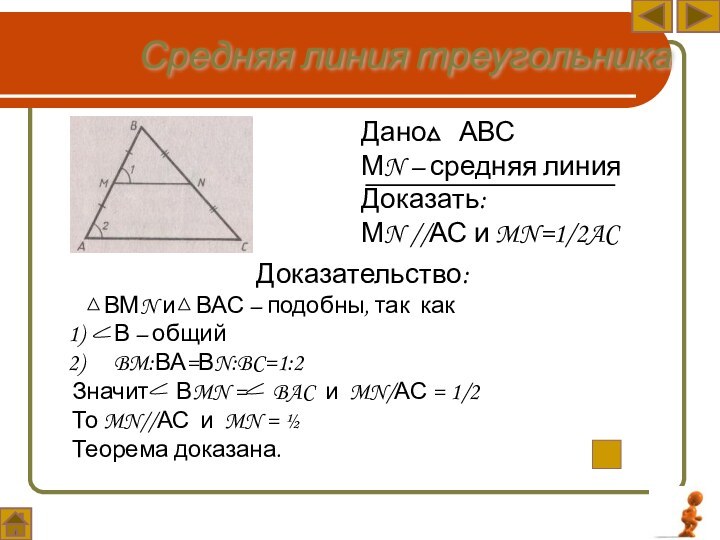
из его сторон и равна половине этой стороны.

Средняя линия треугольника




Слайд 24 Дано: АВС
МN – средняя линия
Доказать:
МN //АС и

Дано: АВСМN – средняя линияДоказать:МN //АС и MN=1/2ACСредняя линия треугольника Доказательство:

MN=1/2AC

Средняя линия треугольника
Доказательство:
ВМN и

ВАС – подобны, так как
В – общий
BM:ВА=ВN:BC=1:2
Значит ВMN = BAC и MN/АС = 1/2
То MN//АС и MN = ½
Теорема доказана.











Слайд 25 Меридианы треугольника пересекаются в одной точке, которая делит

Меридианы треугольника пересекаются в одной точке, которая делит каждую меридиану в

каждую меридиану в отношении 2:1, считая от вершины.
Медианы

в треугольнике

Дано: АВС
т.О – пересечение медиан
ВВ1 и АА1
Доказать:





Слайд 26 Доказательство:
А1В1 – средняя линия, и А1В1//АВ, поэтому

Доказательство:А1В1 – средняя линия, и А1В1//АВ, поэтому

и

Значит АОВ А1ОВ1(по двум углам),то
Но АВ=А1В1, поэтому АО=2А1О и ВО=2В1О. Значит точка О- пересечение медиан АА1 и ВВ1 делит каждую из них в отношении 2:1, считая от вершины.
Аналогично доказывается, что точка О – пересечение медиан ВВ1 и СС1 делит каждую из них в отношении 2:1, считая от вершины.
Значит точка О – пересечения медиан АА1, ВВ1и СС1 делит их в отношении 2:1, считая от вершины.




Медианы в треугольнике





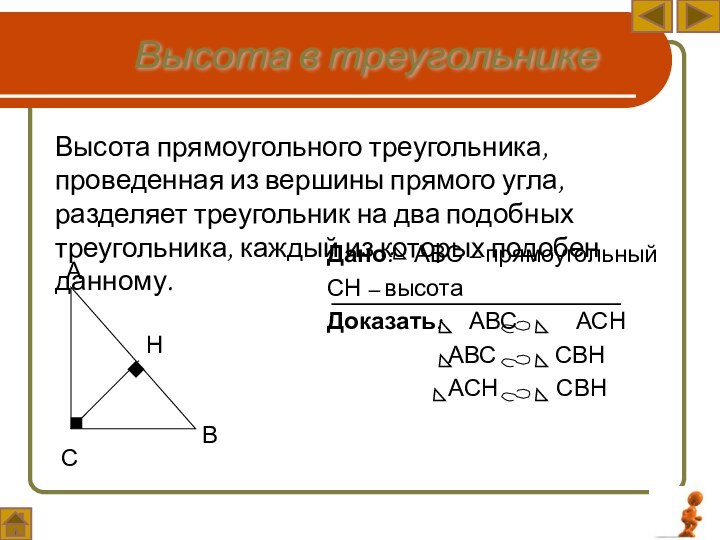
Слайд 27 Высота прямоугольного треугольника, проведенная из вершины прямого угла,

Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на

разделяет треугольник на два подобных треугольника, каждый из которых

подобен данному.




Высота в треугольнике




Н

В

С

А

Дано: АВС – прямоугольный
СН – высота
Доказать: АВС АСН
АВС СВН
АСН СВН











Слайд 28 Доказательство:
АВС АСН(по двум

Доказательство: АВС АСН(по двум углам: А- как общий и

углам: А- как общий и прямым),
АВС

ВСН(по двум углам: В- общий и прямыми),
Рассмотрим АСН и ВСН – прямоугольные
1) угол АНС = углу СНВ – прямые углы
2) угол А = углу ВСН
Значит АСН ВСН.




Высота в треугольнике













Слайд 29 Отрезок ХY называется средним пропорциональным (или средним геометрическим)

Отрезок ХY называется средним пропорциональным (или средним геометрическим) между отрезками АВ и СД, еслиСреднее пропорциональное

между отрезками АВ и СД, если



Среднее пропорциональное

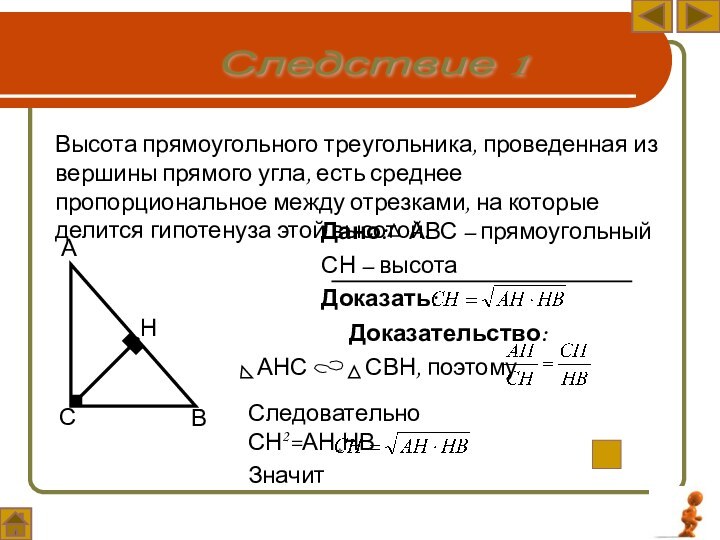
Слайд 30 Дано: АВС – прямоугольный
СН – высота
Доказать:
Высота прямоугольного

Дано: АВС – прямоугольныйСН – высотаДоказать:Высота прямоугольного треугольника, проведенная из вершины

треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное

между отрезками, на которые делится гипотенуза этой высотой.




Следствие 1


С



Н

А

В


Доказательство:
АНС СВН, поэтому


Следовательно СН2=АН*НВ
Значит





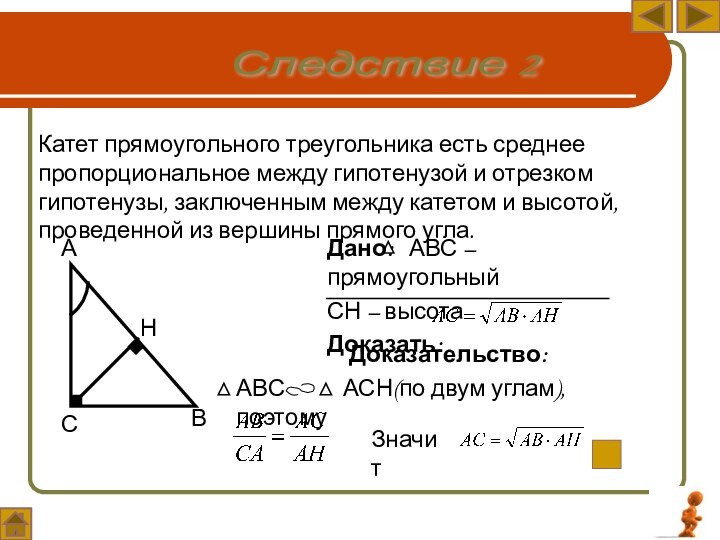
Слайд 31 Дано: АВС – прямоугольный
СН – высота
Доказать:
Катет прямоугольного

Дано: АВС – прямоугольныйСН – высотаДоказать:Катет прямоугольного треугольника есть среднее пропорциональное

треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,

заключенным между катетом и высотой, проведенной из вершины прямого угла.




Следствие 2




С

В

Н

Доказательство:
АВС АСН(по двум углам), поэтому

Значит





А



Слайд 32


Соотнашение между сторонами и углами прямоугольного треугольника
Синус

Соотнашение между сторонами и углами прямоугольного треугольника Синус Косинус Тангенс Значение


Косинус
Тангенс
Значение синуса, косинуса и тангенса для углов

30, 45 и 60 градусов.

Котангенс

Основные тригонометрические тождества.

Слайд 33


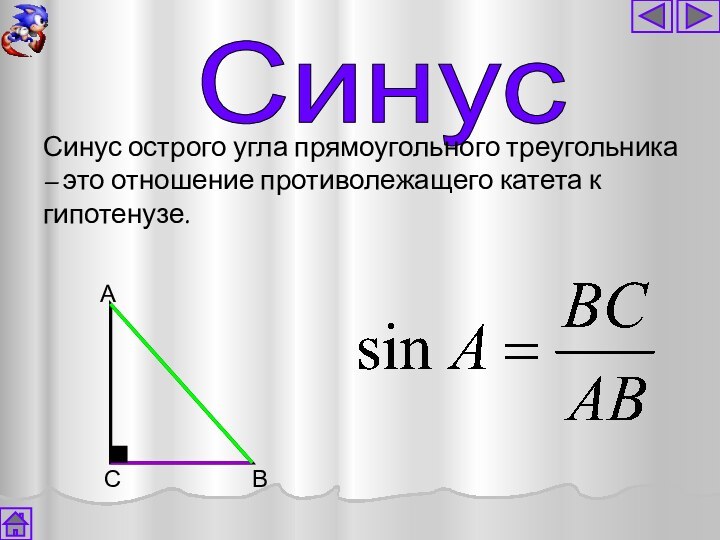
Синус
Синус острого угла прямоугольного треугольника – это

Синус Синус острого угла прямоугольного треугольника – это отношение противолежащего катета к гипотенузе. АСВ

отношение противолежащего катета к гипотенузе.


А
С
В

Слайд 34




А
В
С
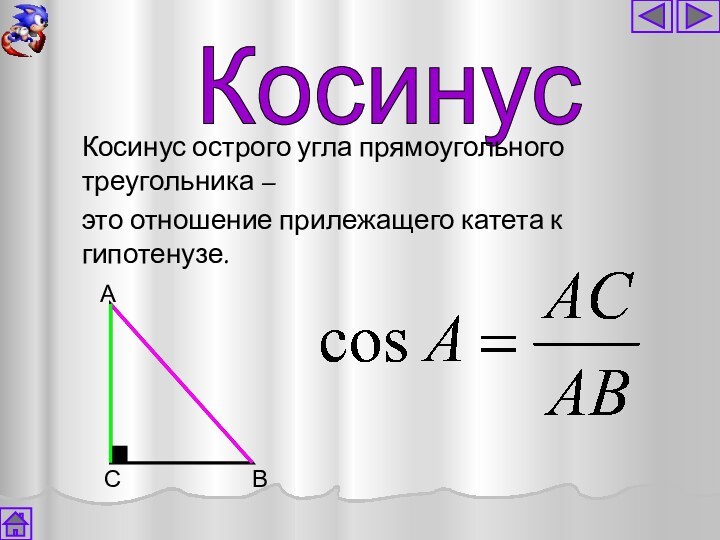
Косинус
Косинус острого угла прямоугольного треугольника –
это

АВСКосинус Косинус острого угла прямоугольного треугольника – это отношение прилежащего катета к гипотенузе.

отношение прилежащего катета к гипотенузе.

Слайд 35




А
В
С
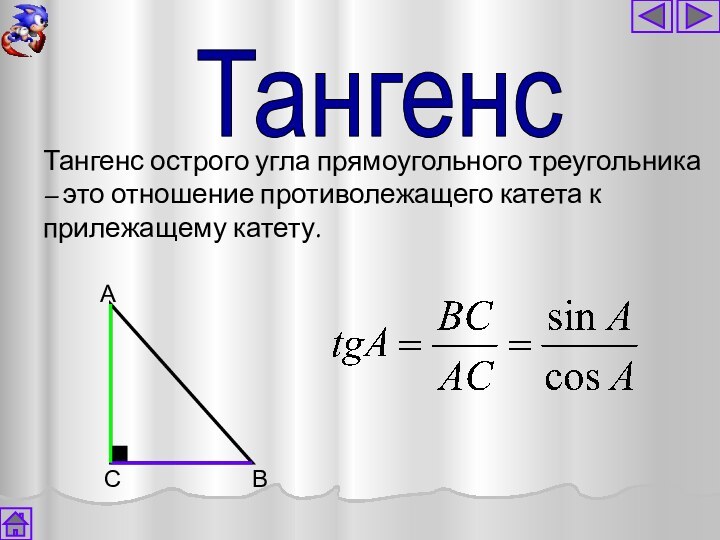
Тангенс
Тангенс острого угла прямоугольного треугольника – это

АВСТангенс Тангенс острого угла прямоугольного треугольника – это отношение противолежащего катета к прилежащему катету.

отношение противолежащего катета к прилежащему катету.

Слайд 36




А
В
С
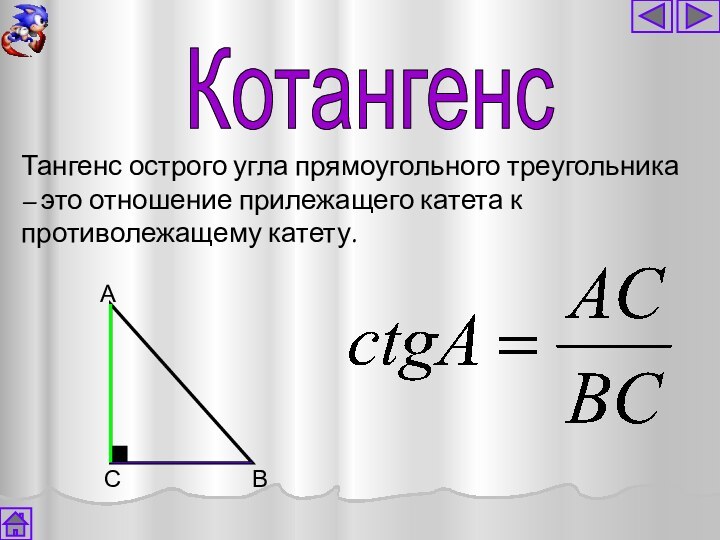
Котангенс
Тангенс острого угла прямоугольного треугольника – это

АВСКотангенс Тангенс острого угла прямоугольного треугольника – это отношение прилежащего катета к противолежащему катету.

отношение прилежащего катета к противолежащему катету.

Слайд 37




А
В
С
Основные тригонометрические тождества.

АВСОсновные тригонометрические тождества.

Слайд 38




А
В
С
Значение синуса, косинуса и тангенса для углов 30,

АВСЗначение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов. АВС – прям.Т.к.вса

45 и 60 градусов.
АВС – прям.



Т.к.


в
с
а

Слайд 39




А
В
С
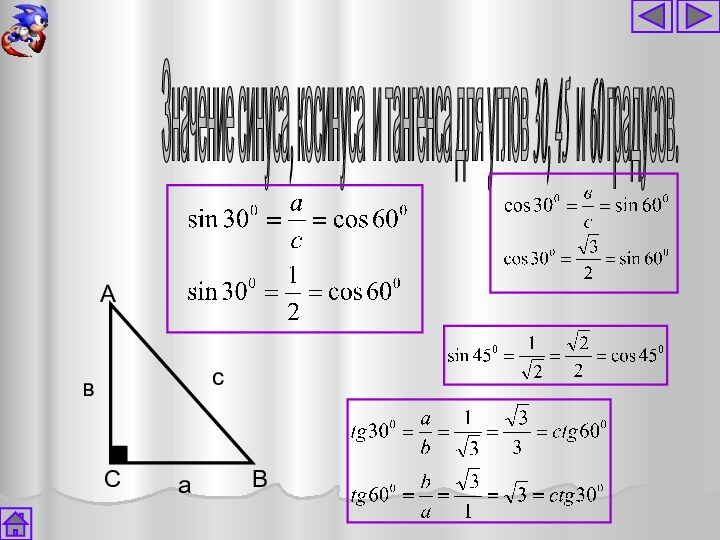
Значение синуса, косинуса и тангенса для углов 30,

АВСЗначение синуса, косинуса и тангенса для углов 30, 45 и 60

45 и 60 градусов.
АВС – прям.





в
с
а
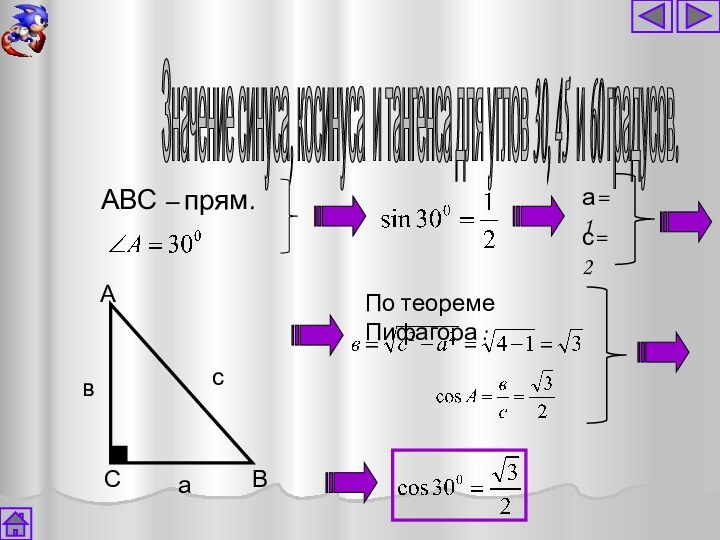
а=1
с=2

По теореме

Пифагора :




Слайд 40




А
В
С
Значение синуса, косинуса и тангенса для углов 30,

АВСЗначение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов. вса

45 и 60 градусов.
в
с
а


Слайд 41




А
В
С
Значение синуса, косинуса и тангенса для углов 30,

АВСЗначение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов. вса

45 и 60 градусов.
в
с
а

  • Имя файла: podobnye-treugolniki.pptx
  • Количество просмотров: 185
  • Количество скачиваний: 0
- Предыдущая Правила создания презентаций
Следующая - Место человека в системе органического мира

Похожие презентации

Площадь прямоугольника 9 класс Площадь прямоугольника 9 класс 149
Теорема Пифагора Теорема Пифагора 148
Презентация по геометрии на тему Подобные треугольники Презентация по геометрии на тему Подобные треугольники 156
Презентация по математике на тему Построение фигур одним росчерком пера. Презентация по математике на тему Построение фигур одним росчерком пера. 248
Решение задач на вычисление площадей фигур Решение задач на вычисление площадей фигур 167
Построение сечений многогранников Построение сечений многогранников 137
Презентация урока на тему Аксиомы стереометрии Презентация урока на тему Аксиомы стереометрии 249
Чертежи разъемных и неразъемных соединений деталей Чертежи разъемных и неразъемных соединений деталей 180
Площадь прямоугольного треугольника Площадь прямоугольного треугольника 147
Признаки равенства прямоугольных треугольников Признаки равенства прямоугольных треугольников 134
Вписанные шары Вписанные шары 207
Ледяной дворец Ледяной дворец 167
Параллельность в пространстве Параллельность в пространстве 177
Виды симметрии Виды симметрии 165
Откладывание вектора от данной точки Откладывание вектора от данной точки 198
Геометрические преобразования в пространстве Геометрические преобразования в пространстве 155
Движения Движения 156
Центральная симметрия Центральная симметрия 166
Тетраэдр Тетраэдр 140
Длина окружности Длина окружности 139
Презентация к уроку математики для 10 класса по теме: Тетраэдр и его сечение Презентация к уроку математики для 10 класса по теме: Тетраэдр и его сечение 168
Презентация Подготовка к ЕГЭ. ШАР. Презентация Подготовка к ЕГЭ. ШАР. 150
Скалярное произведение векторов Скалярное произведение векторов 204
Презентация проекта урока по геометрии Свойства параллелограмма Презентация проекта урока по геометрии Свойства параллелограмма 168
Квадрат Полибия Квадрат Полибия 257
Урок №6 Измерение отрезков п.п.7,8 Урок №6 Измерение отрезков п.п.7,8 150
Правильные многогранники Правильные многогранники 189
Презентация по геометрии по материалам ОГЭ Презентация по геометрии по материалам ОГЭ 141
Симметрия и симметричные фигуры Симметрия и симметричные фигуры 243
Презнтация к уроку геометрии в 7 классе Равнобедренный треугольник и его свойства. Презнтация к уроку геометрии в 7 классе Равнобедренный треугольник и его свойства. 164