- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку на тему: Объём призмы и цилиндра (11 класс)
Содержание
- 2. задачи на урок:повторить формулы для вычисления объема
- 3. Объем ПРЯМОЙ призмы И ЦИЛИНДРА
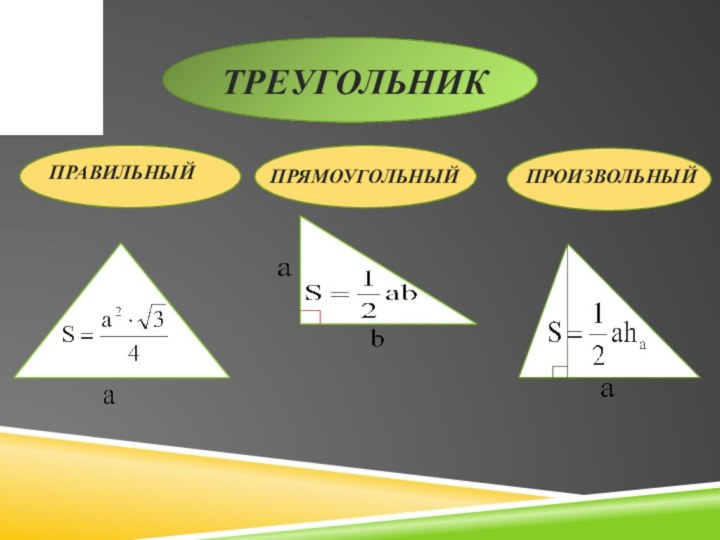
- 4. ТРЕУГОЛЬНИКПРАВИЛЬНЫЙПРЯМОУГОЛЬНЫЙПРОИЗВОЛЬНЫЙ
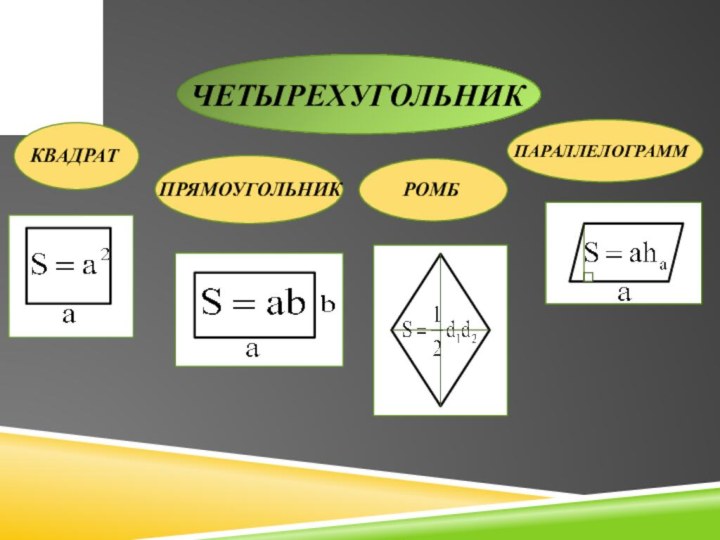
- 5. ЧЕТЫРЕХУГОЛЬНИККВАДРАТПРЯМОУГОЛЬНИКРОМБПАРАЛЛЕЛОГРАММ
- 6. ПРАВИЛЬНЫЙ ШЕСТИУГОЛЬНИК
- 7. Основанием прямой треугольной призмы служит прямоугольный треугольник
- 8. Найдите объем правильной шестиугольной призмы, стороны основания
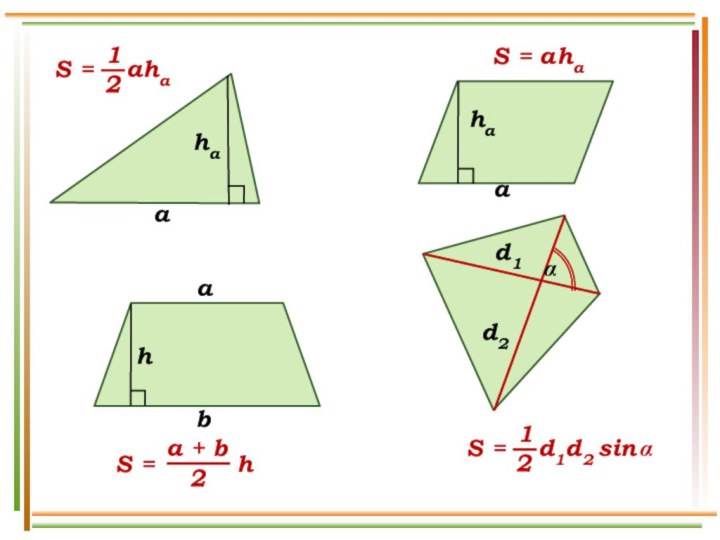
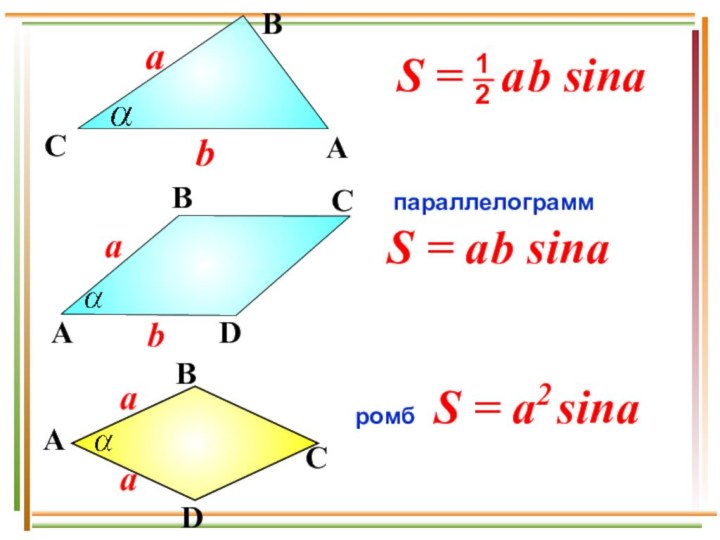
- 9. haS = ahabhad2d1αaha
- 10. S = a2 sinaпараллелограммромбS = a b sina
- 11. 783453
- 12. Теорема ПикаПусть L − число целочисленных точек
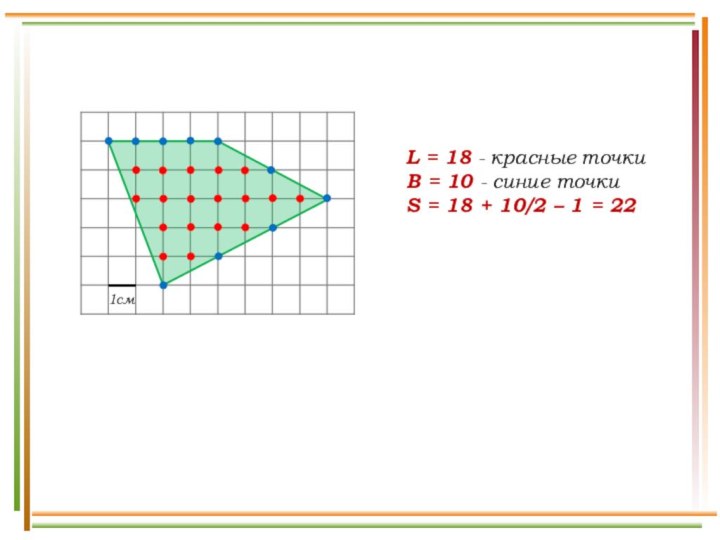
- 13. L = 18 - красные точкиB =
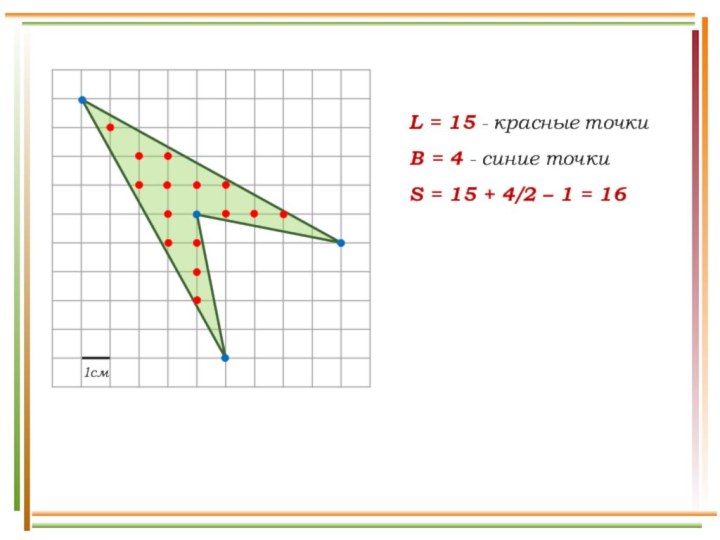
- 14. L = 15 - красные точкиB =
- 15. L = 16 - красные точкиB =
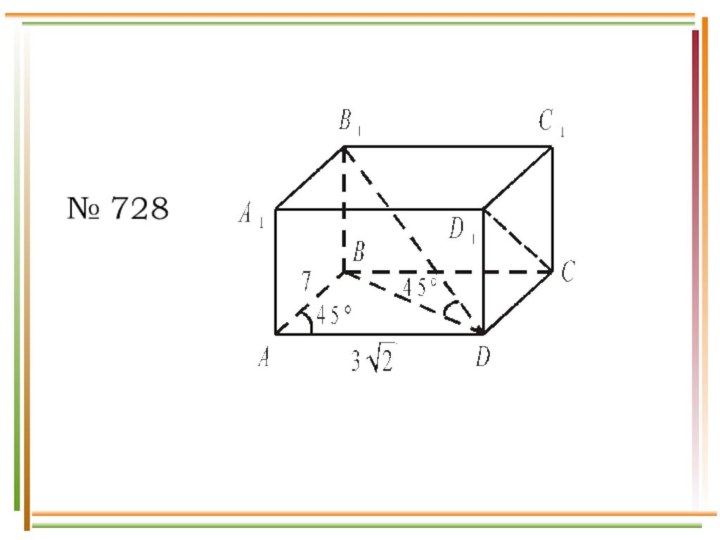
- 16. № 728
- 17. Объём Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action Цилиндр, призма
- 18. В цилиндрический сосуд налили 1200 см3 воды, уровень
- 19. В цилиндрическом сосуде уровень
- 20. Скачать презентацию
- 21. Похожие презентации
задачи на урок:повторить формулы для вычисления объема прямой призмы и цилиндра;учиться применять формулы для вычисления объема прямой призмы и цилиндра при решении задач.











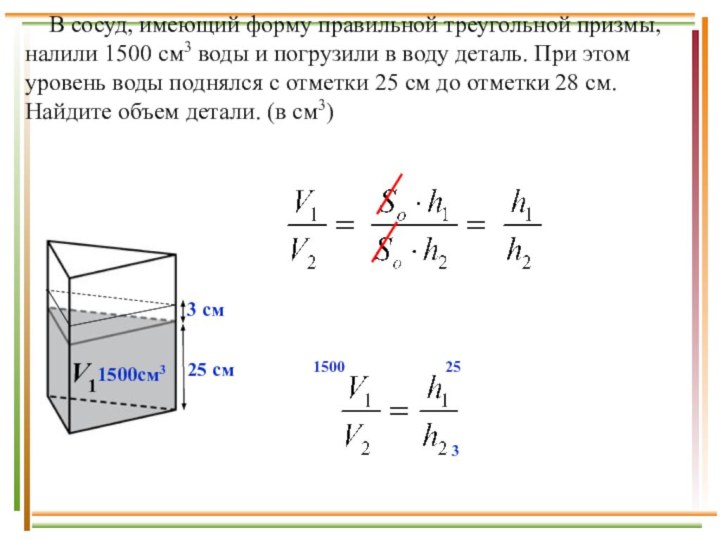
Слайд 2
задачи на урок:
повторить формулы для вычисления объема прямой
призмы и цилиндра;
призмы и цилиндра при решении задач.Слайд 7 Основанием прямой треугольной призмы служит прямоугольный треугольник с
катетами 6 и 8, боковое ребро равно 5. Найдите
объем призмы.ЗАДАЧА 1 (27082)
Слайд 8 Найдите объем правильной шестиугольной призмы, стороны основания которой
равны 1, а боковые ребра равны √3.
ЗАДАЧА 2 (27084)
Слайд 12
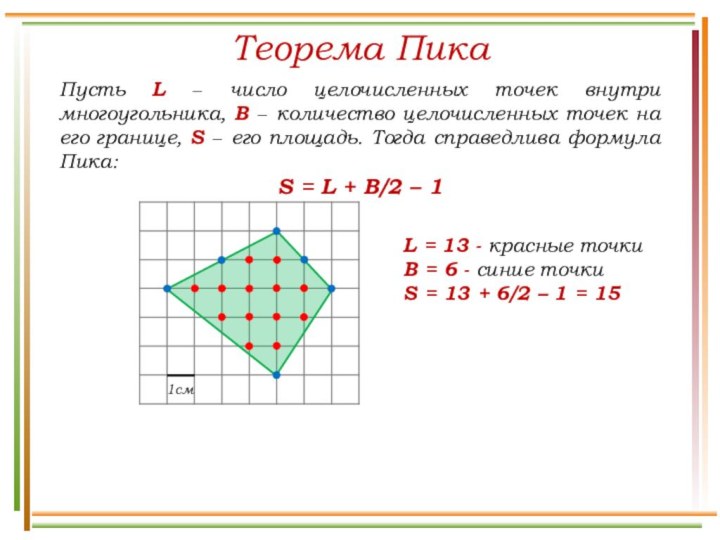
Теорема Пика
Пусть L − число целочисленных точек внутри
многоугольника, B − количество целочисленных точек на его границе,
S − его площадь. Тогда справедлива формула Пика:S = L + B/2 – 1
L = 13 - красные точки
B = 6 - синие точки
S = 13 + 6/2 – 1 = 15
Слайд 17
Объём
Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action
Цилиндр,
призма
Слайд 18 В цилиндрический сосуд налили 1200 см3 воды, уровень воды
при этом достигает высоты 12 см. В жидкость полностью
погрузили деталь, при этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали? (в см3)1200
12
10
Слайд 19 В цилиндрическом сосуде уровень жидкости
достигает 27 см. На какой высоте будет находиться уровень
жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого? (в см)27
V
d
3d