Презентация на тему Пирамида. Сечения пирамиды

Содержание

3. Через вершину А прямоугольника ABCD проведена плоскость
4. Способы задания плоскостиABCabACBAab
5. Признак перпендикулярности прямой и плоскостиabc
6. Теорема о трех перпендикулярахABcC
7. Двугранный угол.Линейный угол двугранного угла.
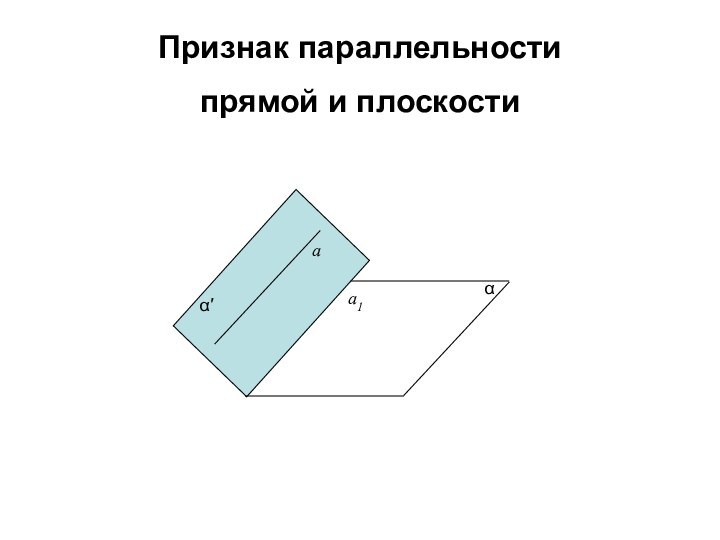
8. Признак параллельности прямой и плоскости
9. Через вершину прямого угла С прямоугольного треугольника
11. XY – ребро двугранного угла (α; ABCD).
12. O1
13. Задача №2. Основанием пирамиды SABC служит равнобедренный
14. Скачать презентацию
15. Похожие презентации

Через вершину А прямоугольника ABCD проведена плоскость α, параллельная диагонали BD. Построить линейный угол двугранного угла, образованного плоскостью прямоугольника ABCD и плоскостью α.

Главная
Геометрия
Пирамида. Сечения пирамиды

Через вершину А прямоугольника ABCD проведена плоскость α, параллельная диагонали BD. Построить

Признак перпендикулярности прямой и плоскостиabc

Двугранный угол.Линейный угол двугранного угла.

Признак параллельности прямой и плоскости

Через вершину прямого угла С прямоугольного треугольника ABC проведена плоскость α параллельная

XY – ребро двугранного угла (α; ABCD). XY || BD – по

Задача №2. Основанием пирамиды SABC служит равнобедренный треугольник ABC, у которого ∠С

Слайды презентации

Слайд 2

Слайд 3
Через вершину А прямоугольника ABCD проведена плоскость α,

Через вершину А прямоугольника ABCD проведена плоскость α, параллельная диагонали BD.

параллельная диагонали BD. Построить линейный угол двугранного угла, образованного

плоскостью прямоугольника ABCD и плоскостью α.

Слайд 4 Способы задания плоскости

A
B
C

a
b

A

C
B
A

a
b

Слайд 5 Признак перпендикулярности прямой и плоскости

a
b
c

Слайд 6 Теорема о трех перпендикулярах

A
B
c
C

Слайд 7 Двугранный угол.
Линейный угол двугранного угла.

Слайд 8 Признак параллельности
прямой и плоскости

Слайд 9 Через вершину прямого угла С прямоугольного треугольника ABC

Через вершину прямого угла С прямоугольного треугольника ABC проведена плоскость α

проведена плоскость α параллельная гипотенузе на расстоянии 1 м

от нее. Катеты AC и BC равны соответственно 6 м и 8 м. Найти двугранный угол между плоскостью треугольника ABC и плоскостью α.

Слайд 10

Слайд 11
XY – ребро двугранного угла (α; ABCD).
XY

XY – ребро двугранного угла (α; ABCD). XY || BD –

|| BD – по условию.
Если AF⊥BD, то AF

⊥ XY.
Т.к. α|| BD, то MN || BD, EF || OO1, тогда EF ⊥ MN, то по т. т. п. AE ⊥ MN.
Значит плоскость (AEF) ⊥ BD, а, следовательно, и XY.
Т.о. ∠FAE – линейный угол двугранного угла с ребром XY.