Презентация на тему по геометрии на тему: Построение треугольника по трем элементам (7 класс)

построение треугольника по трем

элементам;
совершенствовать навыки решения задач на построение.

: на данном луче от его начала отложить отрезок,

равный данному.
Решение.
Изобразим фигуры, данные в условии задачи: луч ОС и отрезок АВ.

Затем циркулем построим окружность радиуса АВ с центром О . Эта окружность пересечет луч ОС в некоторой точке D.
С
С
Отрезок OD – искомый.

О

С

А

В

О

D

угол, равный данному.

Решение.
Изобразим фигуры, данные в условии: угол с вершиной А и луч ОМ.


Проведем окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С.

А

О

М

В

С

А

центром в начале данного луча ОМ. Она пересекает луч

в точке D. После этого построим окружность с центром D, радиус, которой равен ВС. Окружности пересекаются в
двух точках. Одну обозначим
буквой Е. Получим угол МОЕ

О

М

D

E

и углу между ними.

Решение:
Прежде всего уточним, как нужно понимать эту задачу, т. е. что здесь дано и что нужно построить.
Даны отрезки Р1Q1, Р2Q2 угол hк .
Р1 Q1

Р2 Q2 h

к

линейки (без масштабных делений) построить такой треугольник АВС, у

которого две стороны, скажем АВ и АС, равны данным отрезкам Р1Q1
и Р2Q2, а угол А между этими сторонами равен данному углу hк.

на ней с помощью циркуля отложим отрезок АВ, равный

отрезку Р1Q1
Затем построим угол ВАМ, равный данному углу hк. (как это сделать, мы знаем).
На луче АМ отложим отрезок АС, равный отрезку Р2Q2, и проведем отрезок ВС.
Построенный треугольник АВС — искомый.
В самом деле, по построению АВ= Р1Q1, АС= Р2Q2, ∠А=∠hк.

самом деле, по построению АВ= Р1Q1, АС= Р2Q2,

∠А=∠hк.

показывает, что при любых данных отрезках Р1Q1, Р2Q2 и

данном неразвернутом угле hк искомый треугольник построить можно. Так как прямую а и точку А на ней можно выбрать произвольно, то существует бесконечно много треугольников, удовлетворяющих условиям задачи. Все эти треугольники равны друг другу (по первому признаку равенства треугольников), поэтому принято говорить, что данная задача имеет единственное решение.

стороне и двум

прилежащим к ней углам.

Р1 Q1
h m

к п

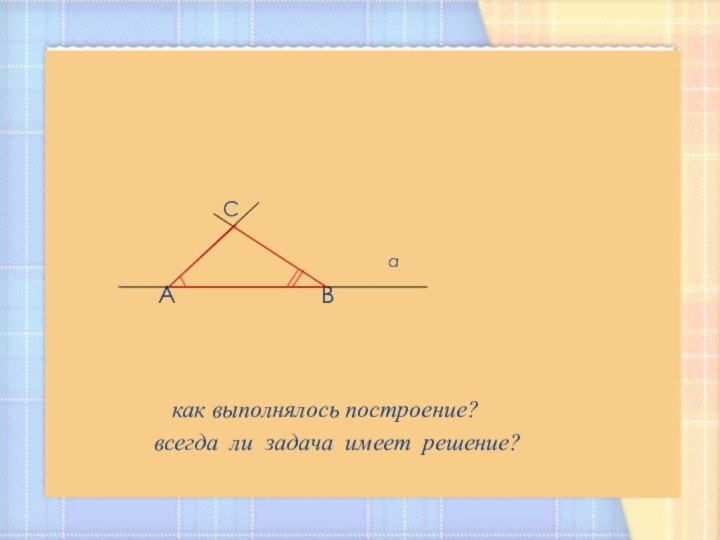
C
a
A B


как выполнялось построение?
всегда ли задача имеет решение?

его сторонам.

Решение.
Пусть даны отрезки Р1Q1, Р2Q2 и Р3Q3. Требуется построить треугольник АВС, в котором
АВ = Р1Q1, AC= Р2Q2, BC= Р3Q3 .
Проведем прямую и на ней с помощью циркуля отложим отрезок АВ, равный отрезку Р1Q1 . Затем построим две окружности: одну — с центром А и радиусом Р2Q2.,

и радиусом Р3Q3 .
Пусть точка

С — одна из точек пересечения этих окружностей. Проведя отрезки АС и ВС, получим искомый треугольник АВС.
Р1 Q1
Р2 Q2

Р3 Q3

C


A B а





Построение треугольника по трем сторонам.

Построенный треугольник АВС, в котором
АВ = Р1Q1, AC= Р2Q2, BC= Р3Q3 .

по построению АВ = Р1Q1,

AC= Р2Q2, BC= Р3Q3 , т.е. стороны треугольника АВС равны данным отрезкам.
Задача 3 не всегда имеет решение.
Действительно, во всяком треугольнике сумма любых двух сторон больше третьей стороны, поэтому если какой-нибудь из данных отрезков больше или равен сумме двух других, то нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.

Рассмотрим схему, по которой обычно решают задачи на построение

с помощью циркуля и линейки.
Она состоит из частей:
1. Отыскание способа решения задачи путём установления связей между искомыми элементами и данными задачи. Анализ дает возможность составить план решения задачи на построение.
2. Выполнение построения по намеченному плану.
3. Доказательство того, что построенная фигура удовлетворяет условиям задачи.
4. Исследование задачи, т.е. выяснение вопроса о том, при любых ли данных задача имеет решение, и если имеет, то сколько решений.

ней углу и биссектрисе треугольника, проведенной из вершины этого

угла.
Решение.
Требуется построить треугольник АВС, у которого одна из сторон, например АС, равна данному отрезку P1Q1, угол А равен данному
углу hк, а биссектриса АD этого треугольника равна данному
отрезку P2Q2.
Даны отрезки P1 Q1 и P2Q2 и угол hк (рисунок а).

P1 Q1 P2 Q2
h
рисунок а
к

Построение (рисунок б).
1) Построим угол ХАУ, равный данному углу hк.
2)На луче АУ отложим отрезок АС, равный данному отрезку P1Q1.
3)Построим биссектрису АF угла ХАУ.
4) На луче АF отложим отрезок АD, равный данному отрезку Р2Q2
5) Искомая вершина В — точка пересечения луча АХ с прямой СD. Построенный треугольник АВС удовлетворяет всем условиям задачи: АС=Р1Q1,
∠А = ∠hк, АD = Р2Q2 , где АD — биссектриса треугольника АВС.

рисунок б

р

А

С

D

B

Y

F

X

Вывод: построенный треугольник АВС удовлетворяет всем условиям задачи:
AC= P1 Q1 ; ∠A=∠hk, AD= P2Q2 ,
где AD - биссектриса треугольника АВС

Вопросы: 18,20 стр. 88.
№ 283, 287.