- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии ТЕОРЕМА О ПЛОЩАДИ ОРТОГОНАЛЬНОЙ ПРОЕКЦИИ
Содержание
теоремаПлощадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекции.




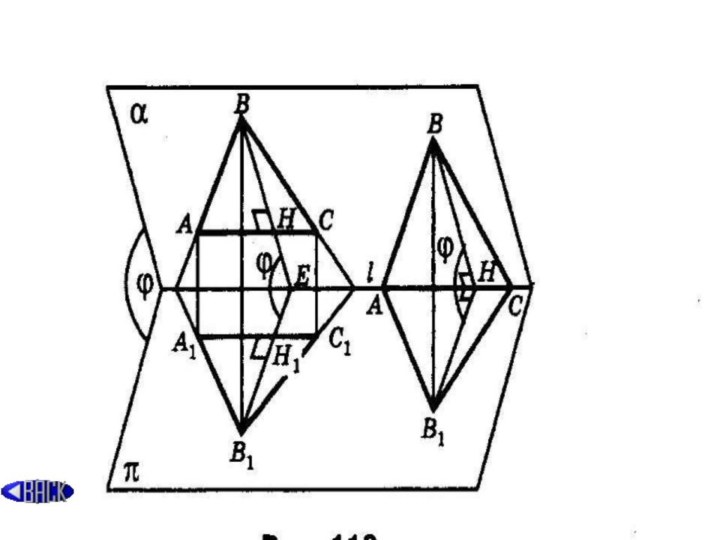




Слайд 4 Доказательство-1. Площадь проекции
треугольника
1. а) пусть одна из сторон, например АС, проектируемого треугольника АВС параллельна прямой L║α∩π Или лежит на ней. Тогда его высота BH перпендикулярна прямой L, а площадь равна ½ AC*BH. На основании выше рассмотренных свойств ортогональной проекции отрезка имеем: AC║L⇒А1С1 ║L; AC = А1С1; B1H1 =ВН*cosϕ.По теореме о трех перпендикулярах прямая B1H1 – ортогональная проекция прямой ВН- перпендикулярна прямой L, следовательно, отрезок B1H1 – высота треугольника А1В1С1. Поэтому SΔA1B1С1= ½А1С1* B1H1= ½ AC * BH* cosϕ=SΔ АВС* cosϕ. Таким образом, SΔA1B1С1 =SΔ АВС* cosϕ. (2)
Слайд 6 б) Ни одна из сторон проектируемого
треугольника АВС не параллельна прямой L.
Проведем через каждую вершину треугольника прямую, параллельную прямой L. Одна = из этих прямых лежит между двумя другими и, следовательно, разбивает треугольник АВС на треугольники ABD и АСD с высотами соответственно BH и СЕ, проведенными к их общей стороне AD (или ее продолжению),которая параллельна L.Прямая m1 – ортогональная проекция прямой m – также разбивает треугольник A1B1С1 – ортогональная проекция треугольника АВС – на треугольники A1B1D1 и А1С1D1 , где А1D1 ║ L, B1H1 ⊥ A1D1, С1Е1 ⊥ A1D1. принимаем во внимание(1) и (2), получаем SΔA1B1С1 = SΔ A1B1D1 + SΔА1С1D1 = SΔ ABD* cosϕ + SΔАСD* cosϕ =(SΔ ABD+ SΔАСD)* cosϕ = SΔ АВС* cosϕ.Итак, для произвольно расположенного в плоскости α треугольник АВС выполняется SΔA1B1С1 = SΔ АВС* cosϕ. (3)
Слайд 8
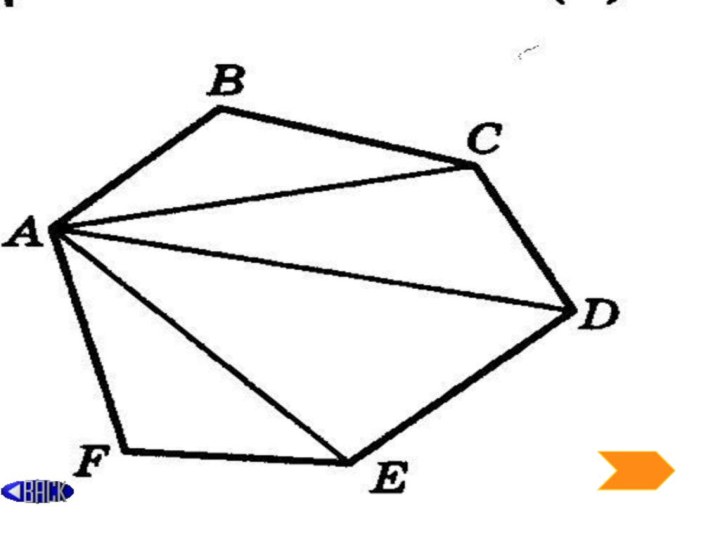
2. Площадь проекции многоугольника. Пусть Ф –
данный выпуклый многоугольник ABCDEF, расположенный в плоскости α. Его
ортогональную проекцию – многоугольник A1B1C1D1E1F1 – обозначим Ф1.Проведя из вершины А многоугольника Ф все его диагонали, разобьём этот многоугольник в объединение непересекающихся треугольников ABC, ACD, ADE, AEF и обозначим их площади соответственно S1, S2, S3 и S4. Тогда для площади Sф многоугольник Ф выполняется Sф = S1+S2+S3+S4.
Аналогичным образом многоугольник Ф1 разобьём в объединение треугольников A1B1C1, A1C1D1, A1D1E1, A1E1F1, площади которых обозначим соответственно S‘1 , S‘2, S‘3 и S‘4. Тогда для площади Sф1 многоугольника Ф1 выполняется Sф1=S‘1+S‘2+S‘3+S‘4. (4)