Презентация на тему Вписанная и описанная окружность

(287-212 ДО Н.Э.) – древнегреческий математик и механик.

Древние математики

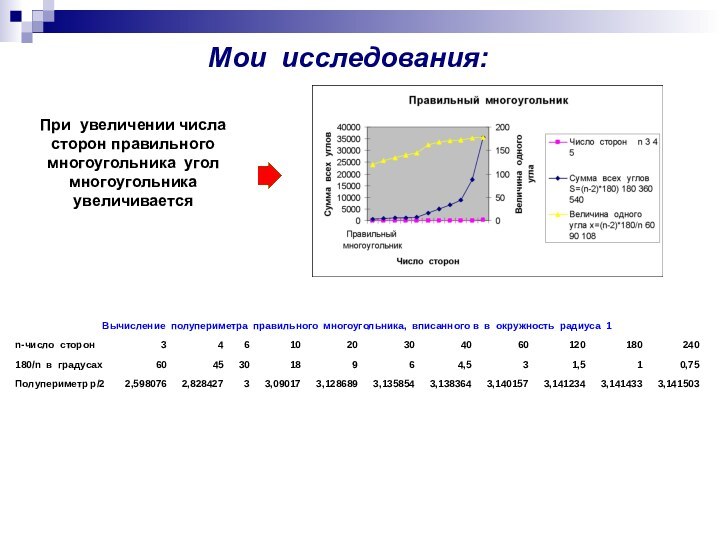
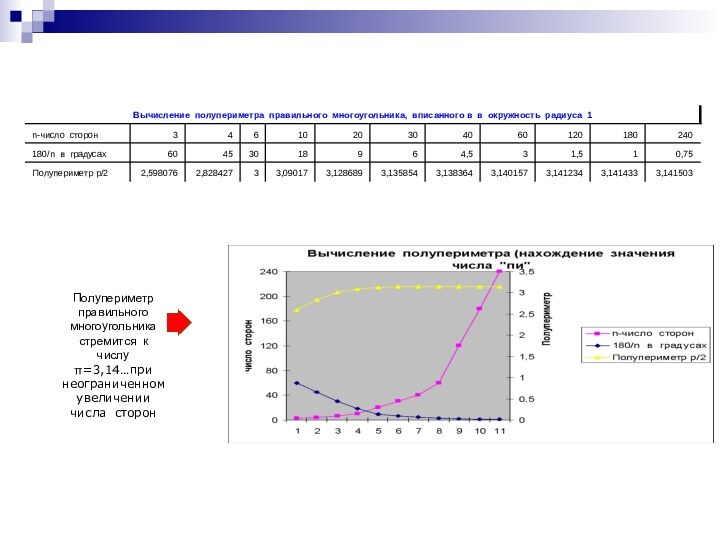
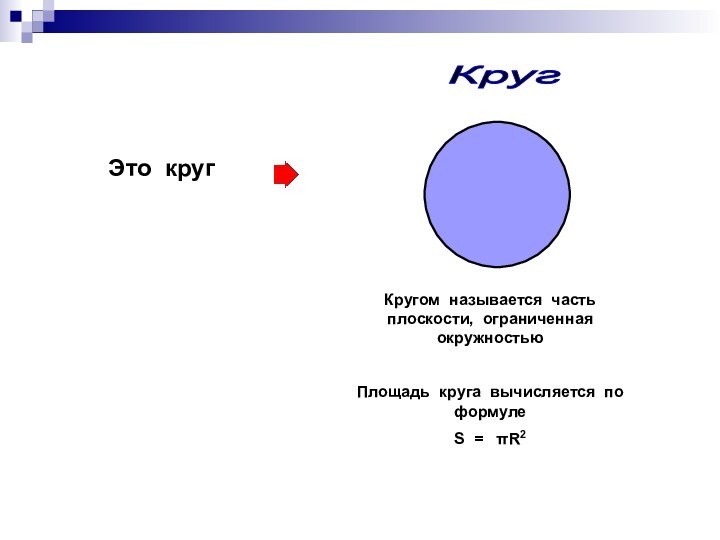
не владели понятиями математического анализа. Однако они умели вычислять длины окружности и некоторых спиралей
Вычисляя периметры правильных вписанных 2n -угольников, Архимед нашёл, что число π, участвующее в формуле длины окружности и площади круга:С=2 π r S= πR2, заключено между 3 10/71 и 31/7, т.е. 3,1408 <π <3,1429

математикой, историей, информатикой, изобразительным искусством, алгеброй и геометрией

Выяснить, действительно ли число π равно 3,14…

в библиотеку

Заочное путешествие в историческую науку и в

историю математики

Сравнивать результаты компьютерного эксперимента с вычислениями учёных древности

многоугольника увеличивается

увеличении числа сторон

что «прямая»?
Нет! Ведь замкнута она


Длина окружности вычисляется

по формуле С = 2πR

Окружность

круга вычисляется по формуле
S = πR2

Круг

правильный многоугольник.
Цель: Изучить теоремы об окружности, описанной около

правильного многоугольника и вписанной в правильный многоугольник

Окружность называется описанной около многоугольника, если все вершины многоугольника лежат на этой окружности

Теорема: Около любого правильного многоугольника можно описать окружность, и притом только одну.

стороны многоугольника касаются этой окружности
Теорема:
В любой правильный многоугольник

можно вписать окружность, и притом только одну.

на размышление:
Задача1:
Докажите, что площадь S треугольника вычисляется по

формуле:
S =½*P*r, где Р - периметр треугольника, к- радиус вписанной окружности.
Задача 2.
Решить задачу: Даны стороны треугольника АВС –а, в, с и площадь S. Выразить радиусы окружностей, описанной около треугольника и вписанной в него, через а, в, с и S

узнали , что правильные многоугольники, окружность и круг встречаются

и применяются в жизни.
В частности, мы узнали что при увеличении числа сторон правильного многоугольника угол многоугольника увеличивается. Полупериметр правильного многоугольника стремится к числу π = 3,14…при неограниченном увеличении числа сторон
Математика своими корнями уходит в далекое прошлое. Мы можем ответить на проблемные вопросы.