- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрия 7 класс
Содержание
- 2. Дано:– иравнобедренныеОпределение:Треугольник называется равнобедренным,если две его стороны равны
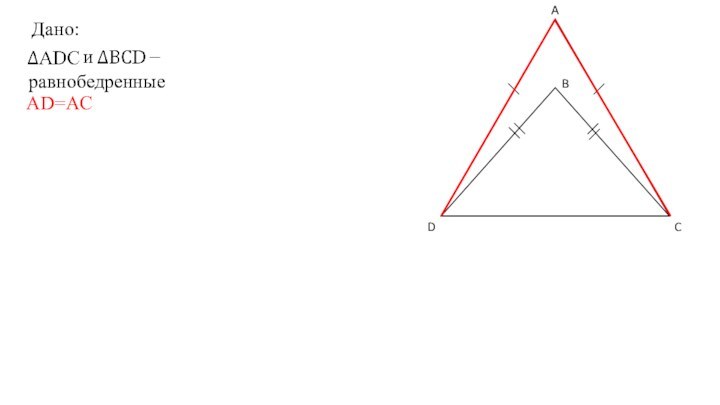
- 3. Дано:– иравнобедренныеAD=AC
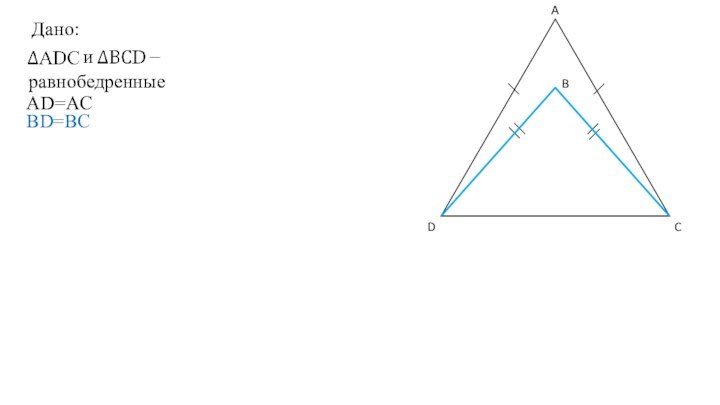
- 4. Дано:– иравнобедренныеAD=ACBD=BC
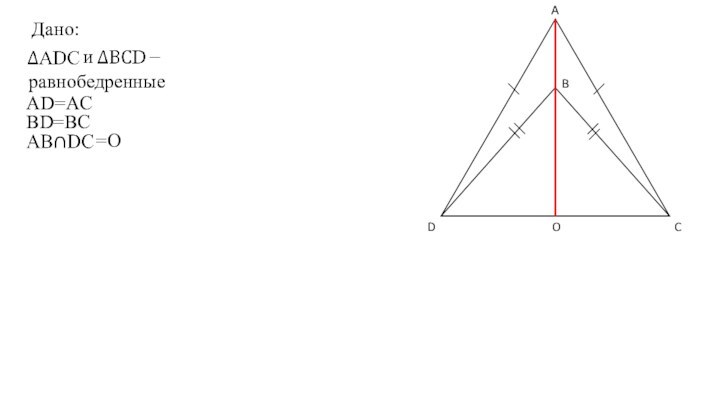
- 5. Дано:– иравнобедренныеAD=ACBD=BCO=O
- 6. Дано:– иравнобедренныеAD=ACBD=BCO=OДоказать:а)∠ADB=∠ACBб) DO=OC
- 7. Дано:– иравнобедренныеAD=ACBD=BCO=OДоказать:б) DO=OCРешение:а)∠ADB=∠ACBAD=AC, DB=BC AB-общая сторона. следовательно ∠ADB=∠ACB, что и требовалось доказать. (по усл.),
- 8. Дано:– иравнобедренныеAD=ACBD=BCO=OДоказать:б) DO=OCРешение:а)∠ADB=∠ACBAD=AC, DB=BC, AB-общая сторона. следовательно
- 9. Скачать презентацию
- 10. Похожие презентации
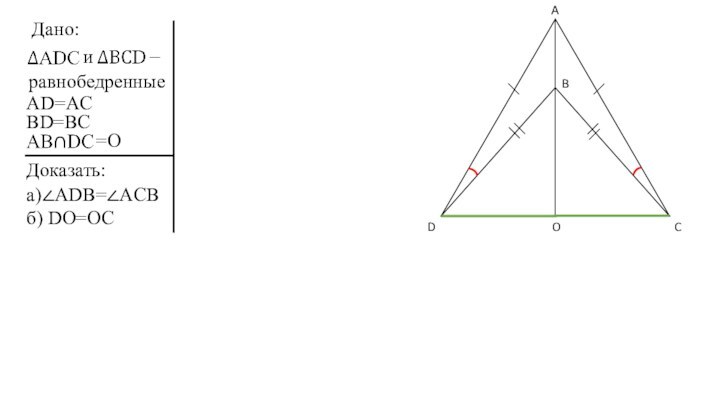
Дано:– иравнобедренныеОпределение:Треугольник называется равнобедренным,если две его стороны равны



Слайд 2
Дано:
–
и
равнобедренные
Определение:
Треугольник называется равнобедренным,
если две его стороны равны
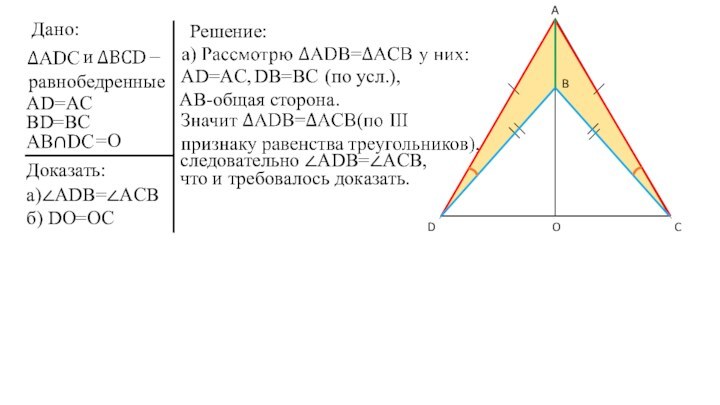
Слайд 7
Дано:
–
и
равнобедренные
AD=AC
BD=BC
O
=O
Доказать:
б) DO=OC
Решение:
а)∠ADB=∠ACB
AD=AC,
DB=BC
AB-общая сторона.
следовательно ∠ADB=∠ACB,
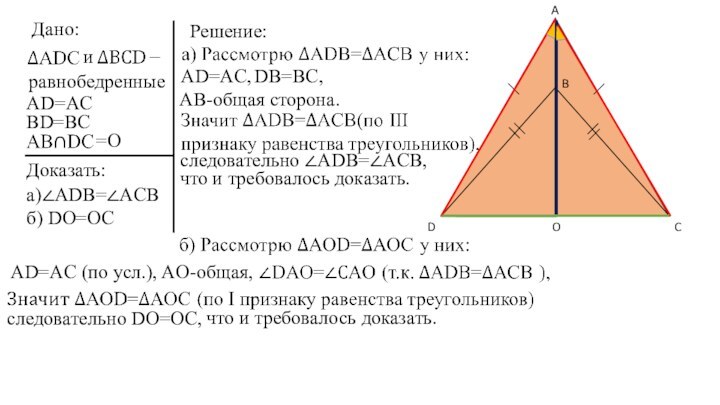
Слайд 8
Дано:
–
и
равнобедренные
AD=AC
BD=BC
O
=O
Доказать:
б) DO=OC
Решение:
а)∠ADB=∠ACB
AD=AC,
DB=BC,
AB-общая сторона.
следовательно ∠ADB=∠ACB,
что и требовалось доказать.
AD=AC (по усл.),
AO-общая,
следовательно DO=OC,
что и требовалось доказать.