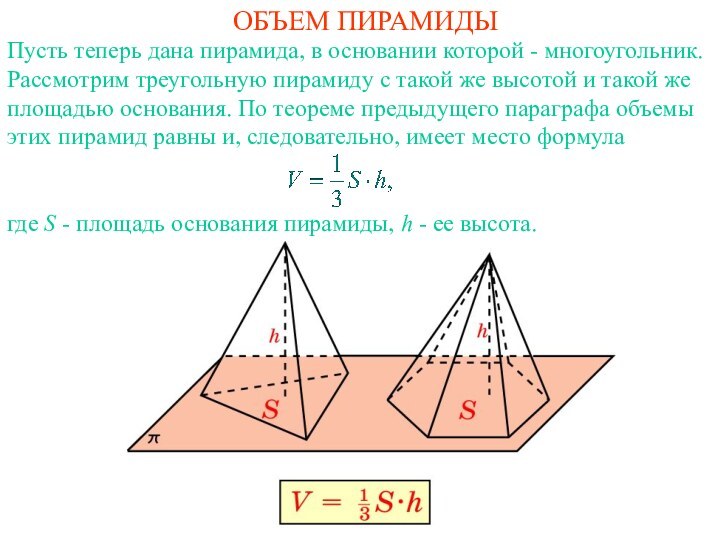
- многоугольник. Рассмотрим треугольную пирамиду с такой же высотой
и такой же площадью основания. По теореме предыдущего параграфа объемы этих пирамид равны и, следовательно, имеет место формулагде S - площадь основания пирамиды, h - ее высота.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


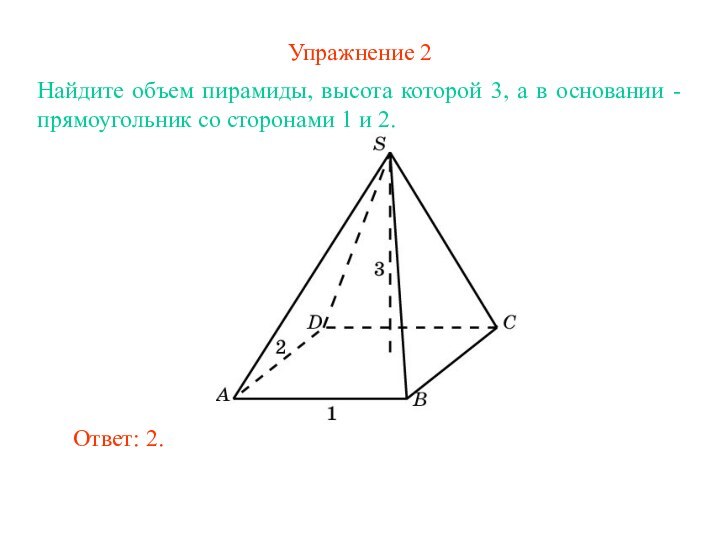
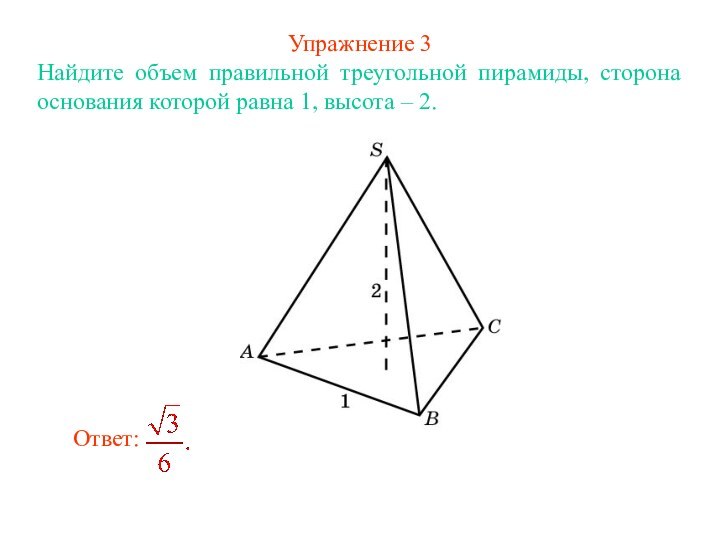

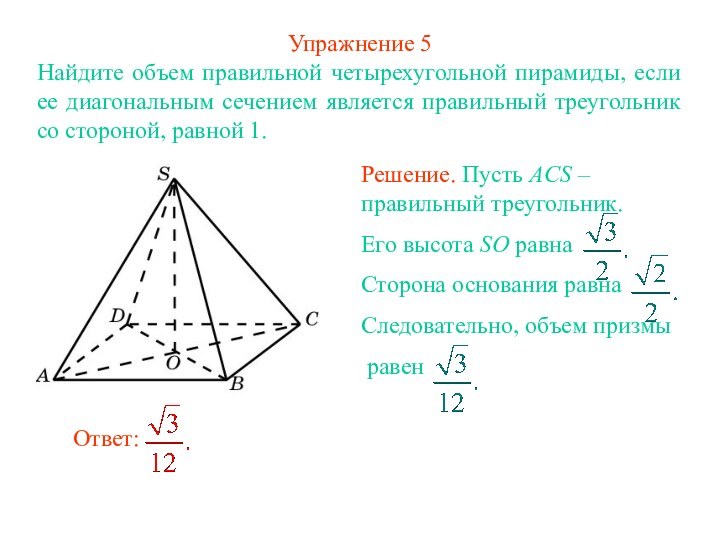
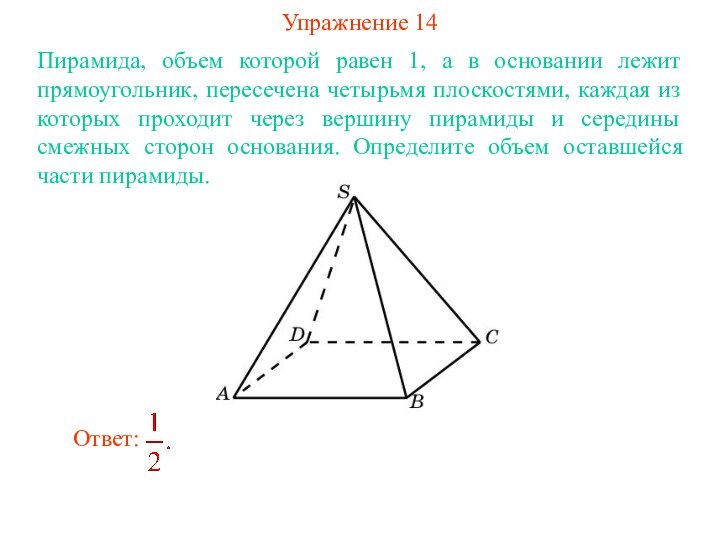


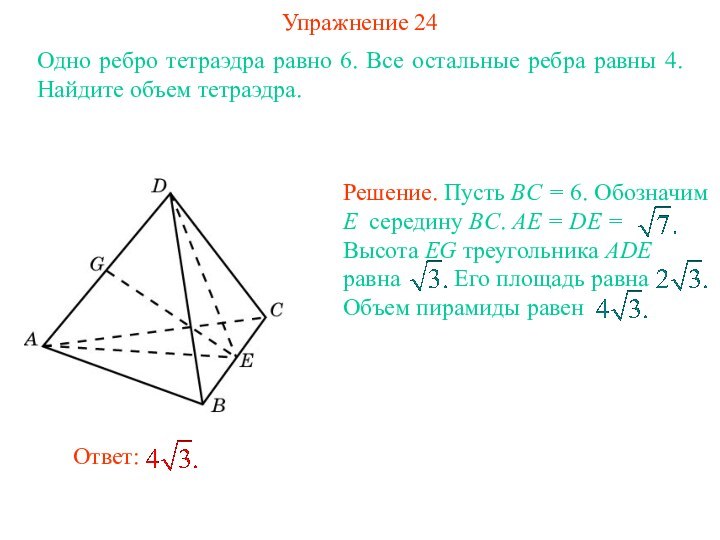





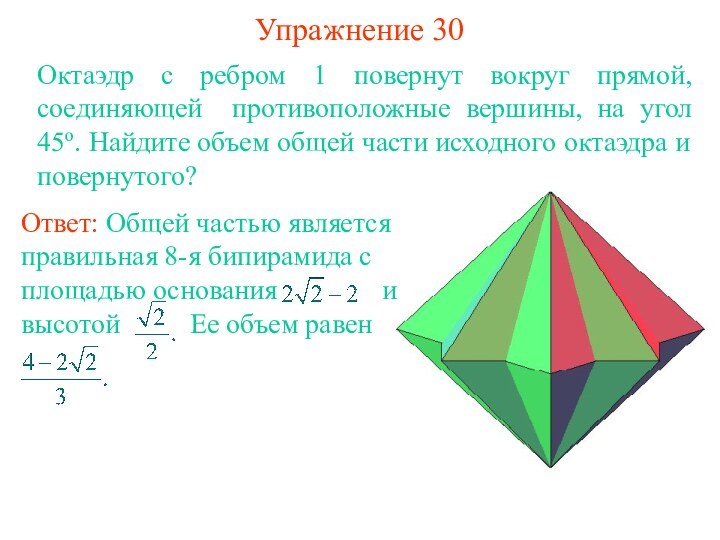
Ответ: Одна треть.
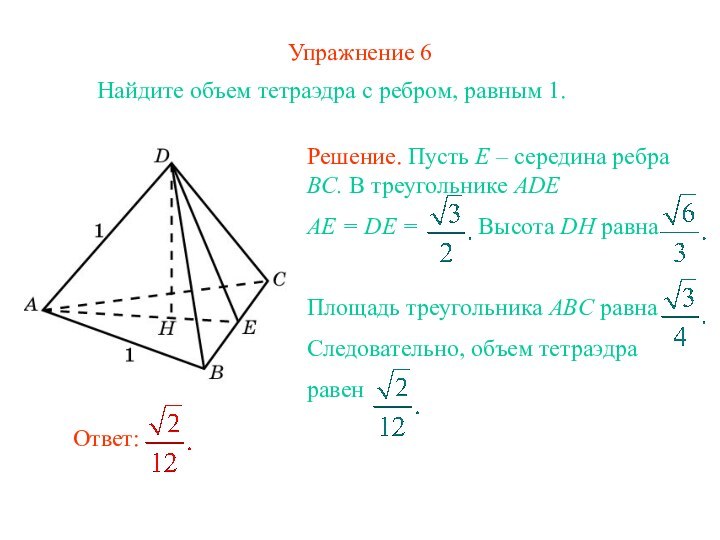
Ответ:
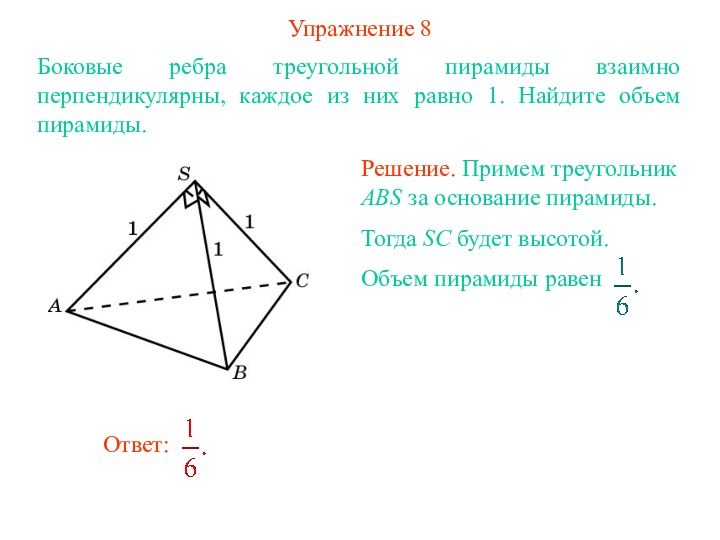
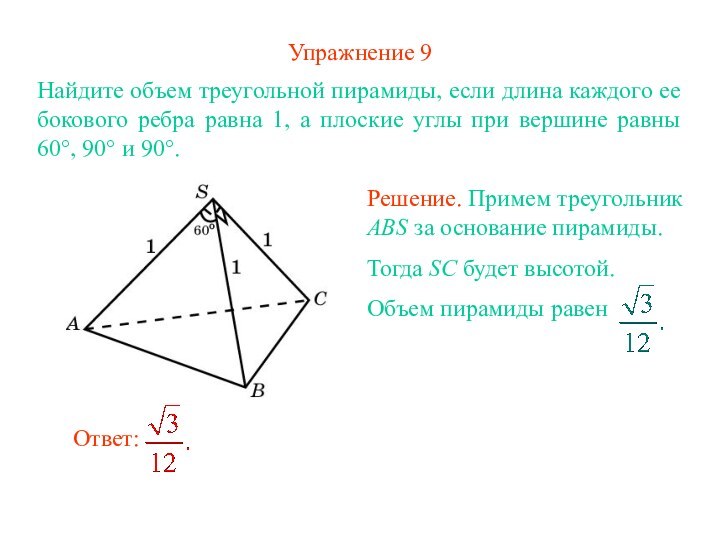
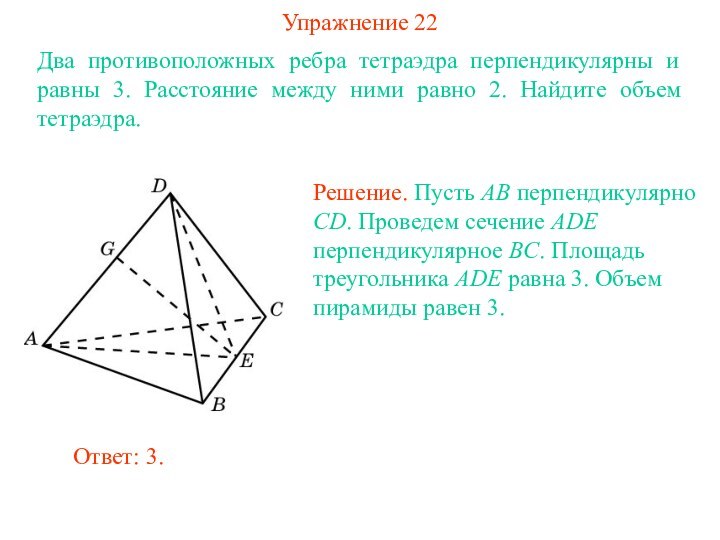
Решение. Примем треугольник ABS за основание пирамиды.
Тогда SC будет высотой.
Объем пирамиды равен
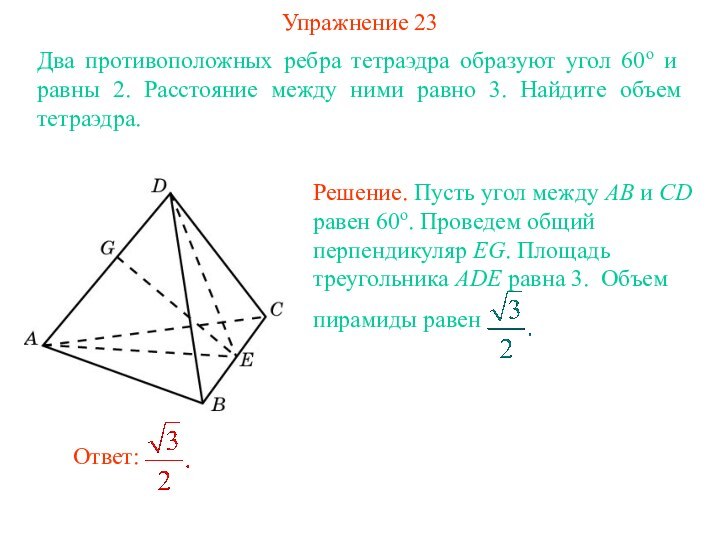
Ответ:
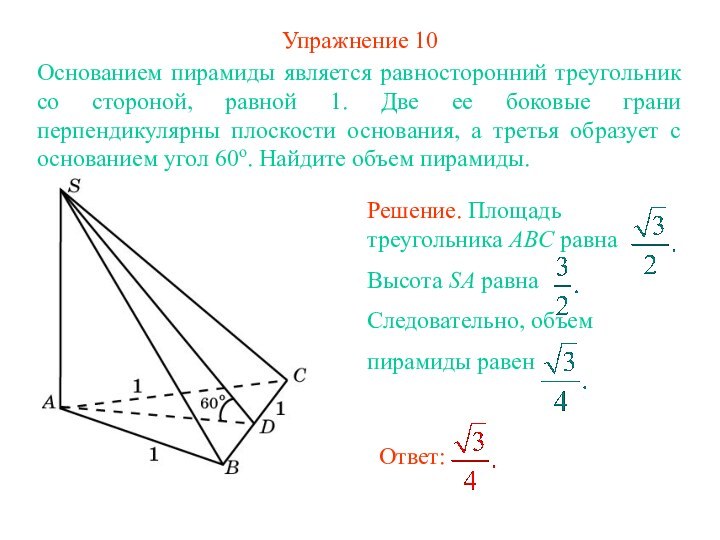
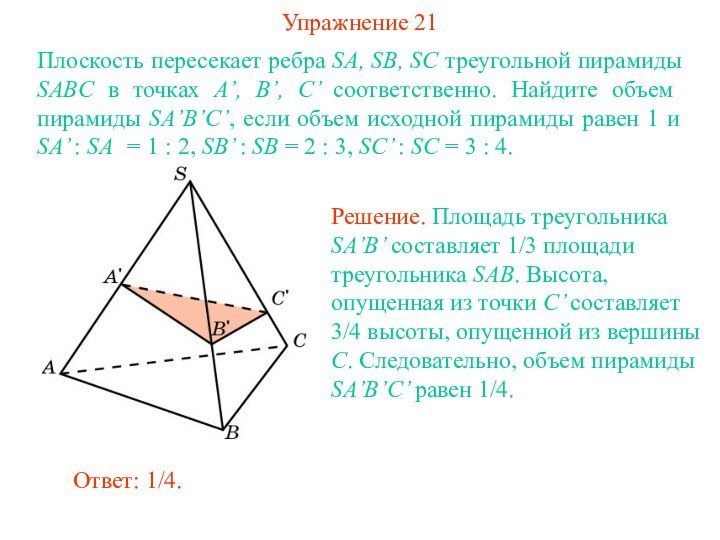
Решение. Площадь треугольника ABC равна
Высота SA равна
Следовательно, объем
пирамиды равен
Ответ:
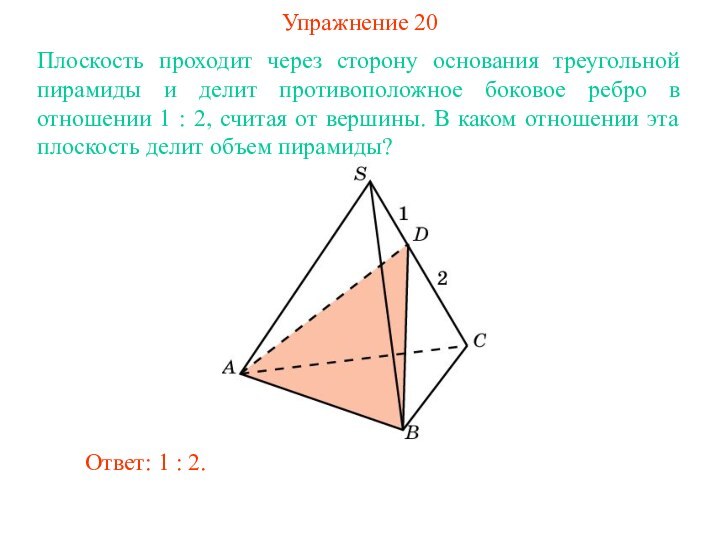
Ответ: 1 : 2.
Ответ: Общая часть является правильной 6-й бипирамидой со стороной основания и
Высотой Объем этой
бипирамиды равен
Ответ: Общей частью является октаэдр (правильная 4-я бипирамида) с ребром
Его объем равен