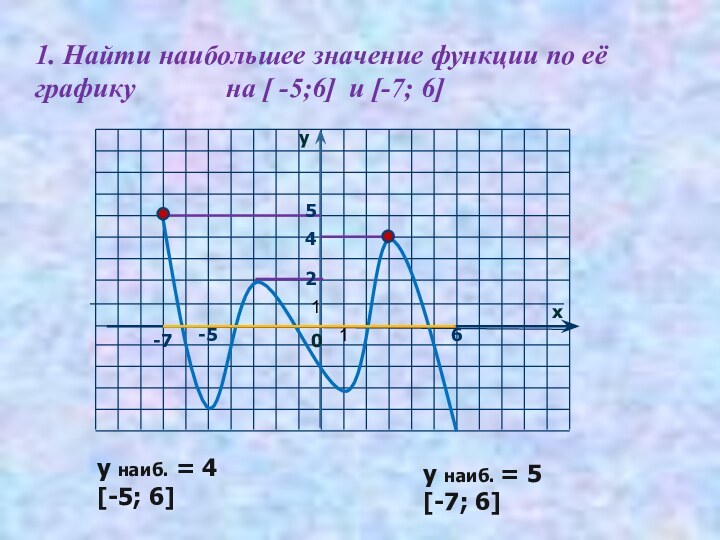
на [ -5;6]
и [-7; 6]5
4
2
-5
у наиб. = 4
[-5; 6]
у наиб. = 5
[-7; 6]
1
1
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






![Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке yyxx000аааbbbY= f(x)Y= f(x)Y= f(x)Функция у = f(х) непрерывна на отрезке [a;b]. Найти](/img/tmb/12/1189421/a55968c8f062aa0aabf5b74b772a0cec-720x.jpg)







5
4
2
-5
у наиб. = 4
[-5; 6]
у наиб. = 5
[-7; 6]
1
1
у наим. =- 3
[-7; 4]
у наим. = -4
[-7; 6]
-3
-2
4
-4
ПРИМЕР. Рекламный щит имеет форму прямоугольника S=9 м2. Изготовьте щит в виде прямоугольника с наименьшим периметром
Цели урока:
Сделать вывод о расположении точек, в которых
функция достигает наибольшего(наименьшего)
значений
3.Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
Задание 1.
Задание 2.
Ответ: : у наим = у (-1) = -13; у наиб = у(1) = 3
3. Вычислить значение функции у= f(x) в точках,
отобранных на втором шаге, и в точках a и b.
Выбрать среди этих значений наименьшее
( это будет унаим )и наибольшее (это будет унаиб )
б) если х = хо – точка минимума,
то унаим= f(xo)