- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Применение подобия к доказательству теорем и решению задач
Содержание
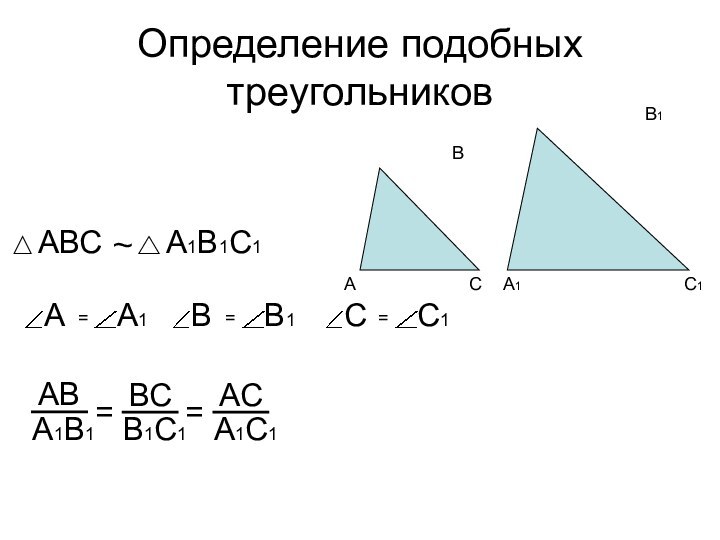
- 2. Определение подобных треугольников~==
- 3. I признак подобия треугольниковДано: Доказать: ~
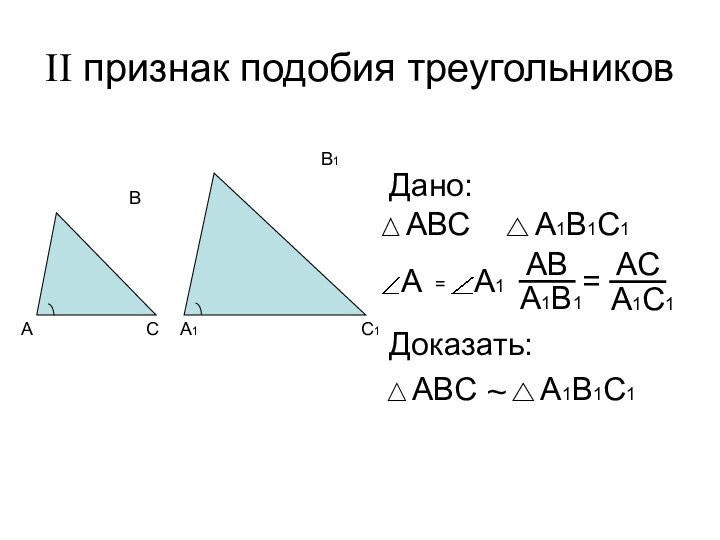
- 4. II признак подобия треугольниковДано: Доказать: =~
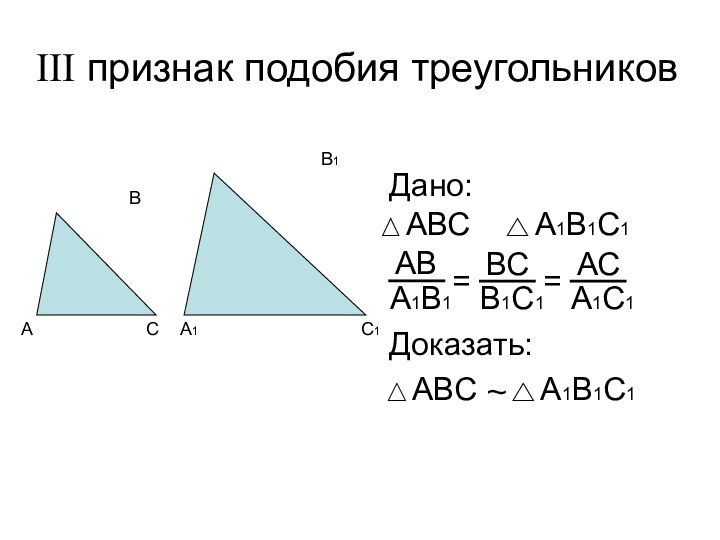
- 5. III признак подобия треугольниковДано: Доказать: ~==
- 6. Задача1АВСДоказать: ~Доказательство:∠В=180°-(∠А+ ∠С)=180°-(30°+80°)=70°∠В= ∠N, ∠C= ∠KΔABC~ΔMNK (по I признаку подобия)
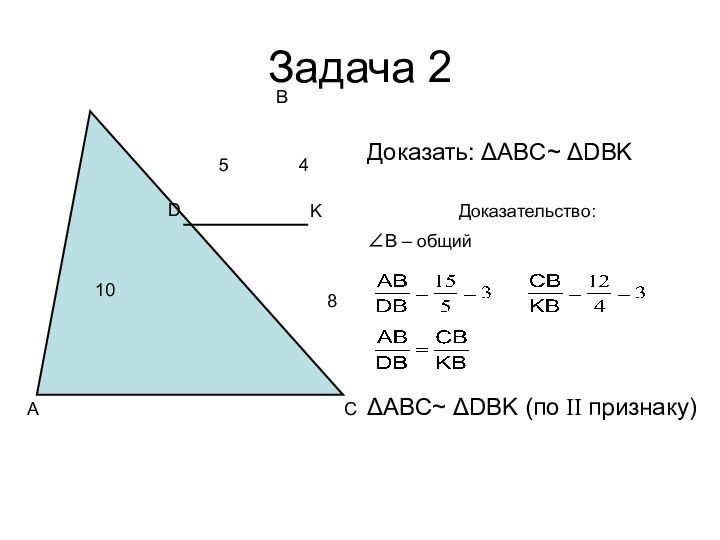
- 7. Задача 2ABCDK48105Доказать: ΔABC~ ΔDBKДоказательство:∠B – общийΔABC~ ΔDBK (по II признаку)
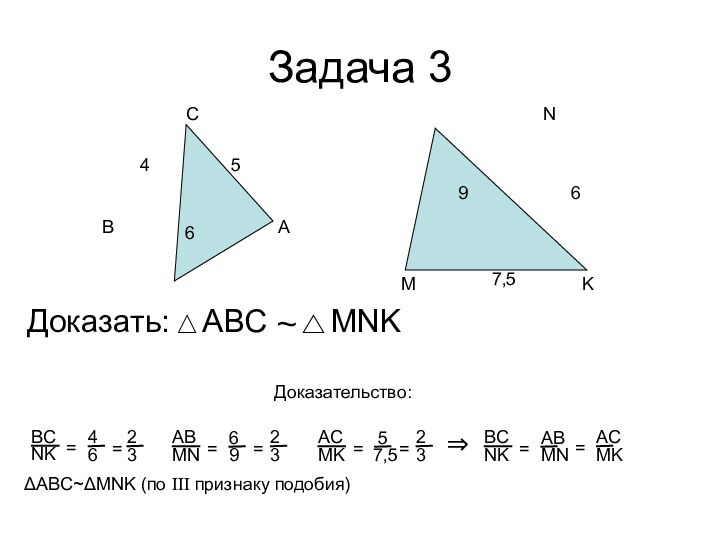
- 8. Задача 3АВСДоказать: ~Доказательство: ΔABC~ΔMNK (по III признаку подобия)456967,5NK=BC64MN=AB96==⇒NK=BCMNAB3232MK=AC7,55=32=MKAC
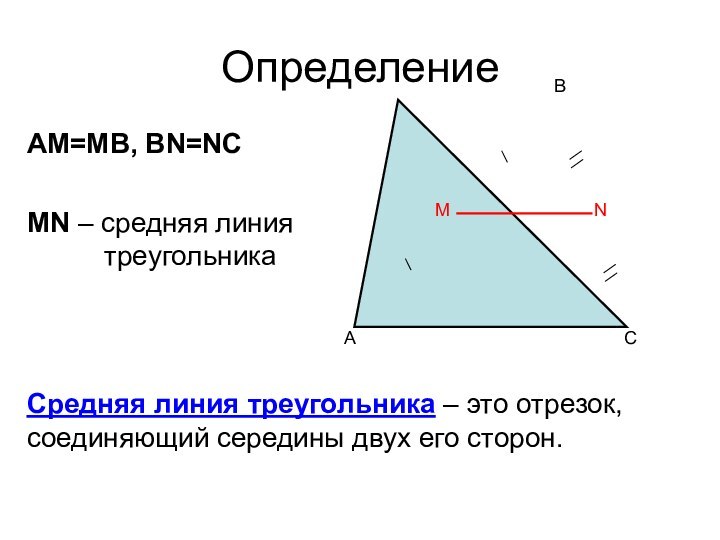
- 9. ОпределениеACBMNAM=MB, BN=NCMN – средняя линия
- 10. Теорема о средней линии треугольникаДано: MN –
- 11. Задача А1ACBMKДано: MK=13см Найти: AB
- 12. Задача А2ABCMNKДано: AB=10cм, ВС=14см, АС=16смНайти: периметр ΔMNK
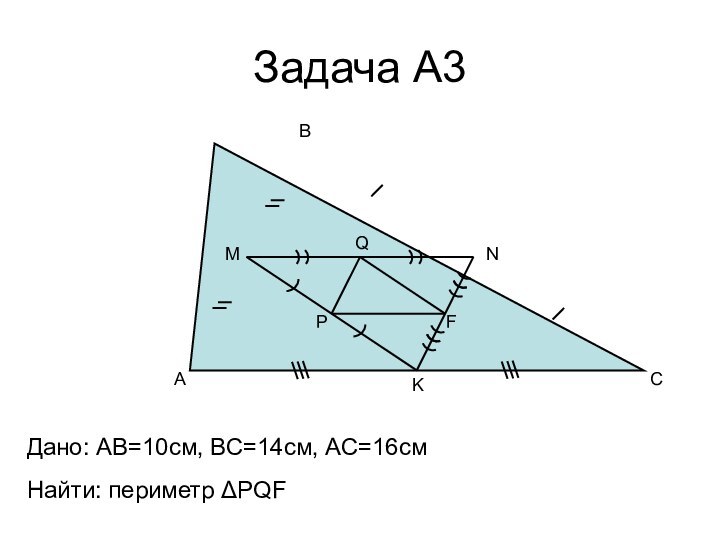
- 13. Задача А3ABCMNKPQFДано: AB=10cм, ВС=14см, АС=16смНайти: периметр ΔPQF
- 14. Задача В1ACBMKДано: PΔMKC =35 см Найти: PΔABC
- 15. Задача В2ABCDOKДано: ABCD – параллелограммAK=KBAK=3см.KO=4см.Найти: периметр ABCD
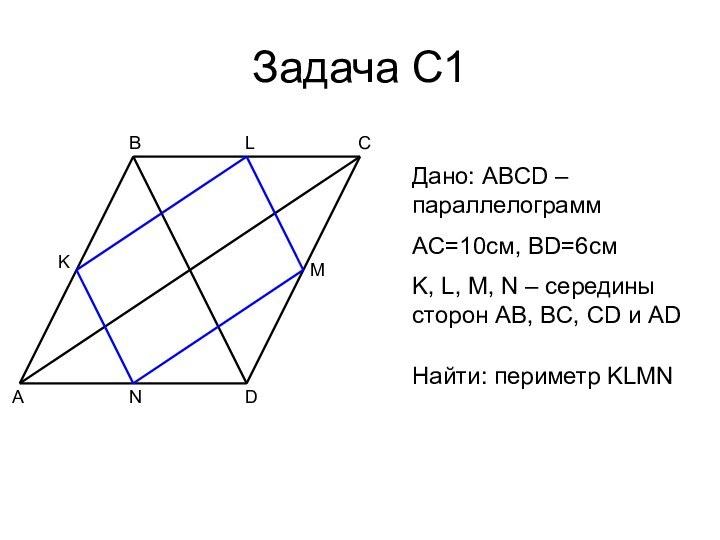
- 16. Задача С1ABCDMNKДано: ABCD – параллелограммAC=10см, BD=6смK, L,
- 17. Задача С2ABCDMNKДано: ABCD – четырёхугольникK, L, M,
- 18. Вариньон Пьер(1654-1722)
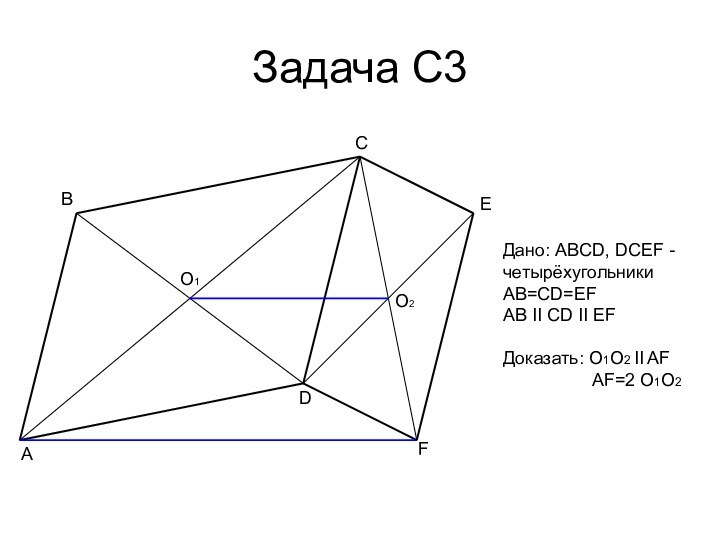
- 19. Задача С3ABCDEFO1O2Дано: ABCD, DCEF - четырёхугольникиAB=CD=EFAB II
- 20. Скачать презентацию
- 21. Похожие презентации
Определение подобных треугольников~==










Слайд 6
Задача1
А
В
С
Доказать:
~
Доказательство:
∠В=180°-(∠А+ ∠С)=180°-(30°+80°)=70°
∠В= ∠N, ∠C= ∠K
ΔABC~ΔMNK (по I
признаку подобия)
Слайд 8
Задача 3
А
В
С
Доказать:
~
Доказательство:
ΔABC~ΔMNK (по III признаку подобия)
4
5
6
9
6
7,5
NK
=
BC
6
4
MN
=
AB
9
6
=
=
⇒
NK
=
BC
MN
AB
3
2
3
2
MK
=
AC
7,5
5
=
3
2
=
MK
AC
Слайд 9
Определение
A
C
B
M
N
AM=MB, BN=NC
MN – средняя линия
треугольника
Средняя линия треугольника – это отрезок, соединяющий
середины двух его сторон.
Слайд 10
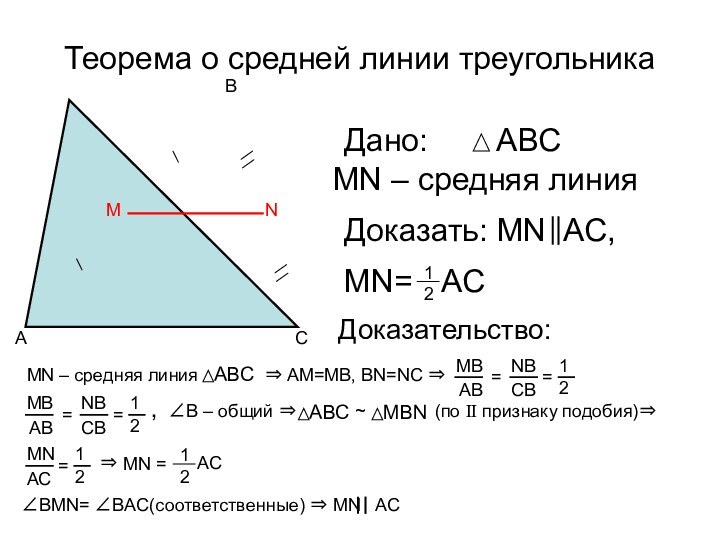
Теорема о средней линии треугольника
Дано:
MN – средняя
линия
Доказать: MN AC,
MN=
1
2
AC
Доказательство:
МN – средняя линия
⇒
AM=MB, BN=NC ⇒ MB
AB
NB
CB
=
=
1
2
MB
AB
NB
CB
=
=
1
2
,
∠B – общий ⇒
~
(по II признаку подобия)⇒
MN
AC
=
1
2
∠BMN= ∠BAC(соответственные) ⇒ MN AC
⇒
MN =
1
2
AC
Слайд 16
Задача С1
A
B
C
D
M
N
K
Дано: ABCD – параллелограмм
AC=10см, BD=6см
K, L, M,
N – середины сторон AB, BC, CD и AD
Найти: периметр KLMN
L
Слайд 17
Задача С2
A
B
C
D
M
N
K
Дано: ABCD – четырёхугольник
K, L, M, N
– середины сторон AB, BC, CD и AD
Доказать:
KLMN - параллелограммL