Презентация на тему по геометрии на тему Теоремы Чевы и Менелая

Содержание

2. На сторонах АС и ВС треугольника АВС
3. Рассмотрим треугольник АВС и отметим
5. Докажем обратное утверждение. Пусть точки С1, А1,
6. Замечание. Мы брали точки А1, В1и С1
7. Теорема Менелая.Менелай Александрийский – древнегреческий математик и
8. Решите задачи.1. Докажите, что медианы треугольника пересекаются
9. 2. Доказать, что в треугольнике биссектрисы пересекаются
10. 3. Доказать, что в треугольнике высоты (или
11. Скачать презентацию
12. Похожие презентации

На сторонах АС и ВС треугольника АВС отмечены точки К и М так, что АК:КС=m:n, ВМ:МС=p:q. Отрезки АМ и ВК пересекаются в точке О. ТогдаНапоминание.Теорема о пропорциональных отрезках в треугольнике.

Главная
Геометрия
Презентация по геометрии на тему Теоремы Чевы и Менелая

Теоремы Чевыи МенелаяУчитель математикиМБОУ лицея №2г. Южно – СахалинскаБокова Т.Н.

На сторонах АС и ВС треугольника АВС отмечены точки К и М

Рассмотрим треугольник АВС и отметим на его сторонах АВ, АС

Презентация по геометрии на тему Теоремы Чевы и Менелая

Докажем обратное утверждение. Пусть точки С1, А1, В1 взяты на сторонах АВ,

Замечание. Мы брали точки А1, В1и С1 на сторонах ВС, СА и

Теорема Менелая.Менелай Александрийский – древнегреческий математик и астроном, живший в 1 в.

Решите задачи.1. Докажите, что медианы треугольника пересекаются в одной точке и точкой

2. Доказать, что в треугольнике биссектрисы пересекаются в одной точке. Дано:

3. Доказать, что в треугольнике высоты (или их продолжения) пересекаются в одной

4. В треугольнике АВС биссектрисы АА1, ВВ1, СС1 пересекаются в точке О,

Слайды презентации

Слайд 2 На сторонах АС и ВС треугольника АВС отмечены

На сторонах АС и ВС треугольника АВС отмечены точки К и

точки К и М так, что АК:КС=m:n, ВМ:МС=p:q. Отрезки

АМ и ВК пересекаются в точке О. Тогда

Напоминание.

Теорема о пропорциональных отрезках в треугольнике.

Слайд 3 Рассмотрим треугольник АВС и отметим на

его сторонах АВ, АС и СА точки С1, А1,

В1.

При каком расположении этих точек отрезки АА1, ВВ1, СС1 пересекаются в одной точке?

Слайд 4

Теорема Чевы
Итальянский инженер и математик (1648 – 1734)

Теорема. Если на сторонах АВ, ВС, СА треугольника АВС взяты соответственно точки С1, А1 и В1, то отрезки АА1, ВВ1 и СС1 пересекаются в одной точке тогда и только тогда, когда

Пусть отрезки АА1, ВВ1, СС1 пересекаются в точке О.

По теореме о пропорциональных отрезках в треугольнике имеем

Слайд 5 Докажем обратное утверждение. Пусть точки С1, А1, В1

Докажем обратное утверждение. Пусть точки С1, А1, В1 взяты на сторонах

взяты на сторонах АВ, ВС, СА так, что выполнено

равенство

Докажем, что отрезки АА1, ВВ1, СС1 пересекаются в одной точке.

Обозначим буквой О точку пересечения отрезков АА1 и ВВ1 и проведем прямую СО. Она пересечет сторону АВ в некоторой точке, которую обозначим С2.
Так как отрезки АА1, ВВ1, СС2 пересекаются в одной точке, то по доказанному ранее

Сопоставляя равенства (1) и (2), приходим к равенству

которое показывает, что точки С1 и С2 делят сторону АВ в одном и том же отношении. Следовательно, точки С1 и С2 совпадают, и, значит, отрезки АА1, ВВ1 и СС1 пересекаются в точке О. Теорема доказан.а

Слайд 6 Замечание. Мы брали точки А1, В1и С1 на

Замечание. Мы брали точки А1, В1и С1 на сторонах ВС, СА

сторонах ВС, СА и АВ треугольника АВС. Если же

только одна из этих точек берется на соответствующей стороне, а две другие – на продолжении сторон, то справедливо следующее утверждение.

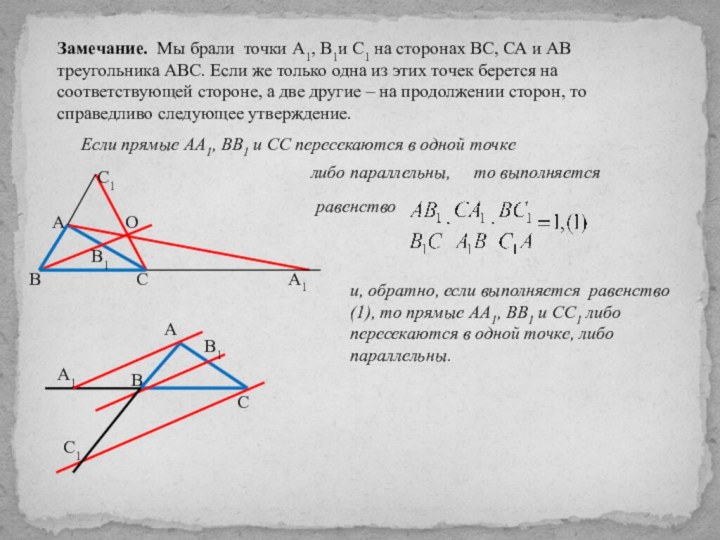
Если прямые АА1, ВВ1 и СС пересекаются в одной точке

либо параллельны,

то выполняется

равенство

и, обратно, если выполняется равенство (1), то прямые АА1, ВВ1 и СС1 либо пересекаются в одной точке, либо параллельны.

Слайд 7 Теорема Менелая.
Менелай Александрийский – древнегреческий математик и астроном,

Теорема Менелая.Менелай Александрийский – древнегреческий математик и астроном, живший в 1

живший в 1 в. н. э
Если на сторонах АВ

и ВС и продолжении стороны АС (либо на продолжениях сторон АВ , ВС и АС) взяты соответственно точки С1, А1 и В1, то эти точки лежат на одной прямой тогда и только тогда, когда