- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Пространственная теорема Пифагора
Содержание
- 2. Все плоские углы тетраэдра ОABC при вершине
- 4. Три формулировки теоремы Пифагора:В прямоугольном треугольнике квадрат
- 5. СA B
- 6. 2.Квадрат длины диагонали прямоугольника равен сумме квадратов
- 7. 3.Квадрат длины любого отрезка равен сумме квадратов
- 8. 2) Спроектируем отрезок A1B1 на прямую а
- 9. Скачать презентацию
- 10. Похожие презентации
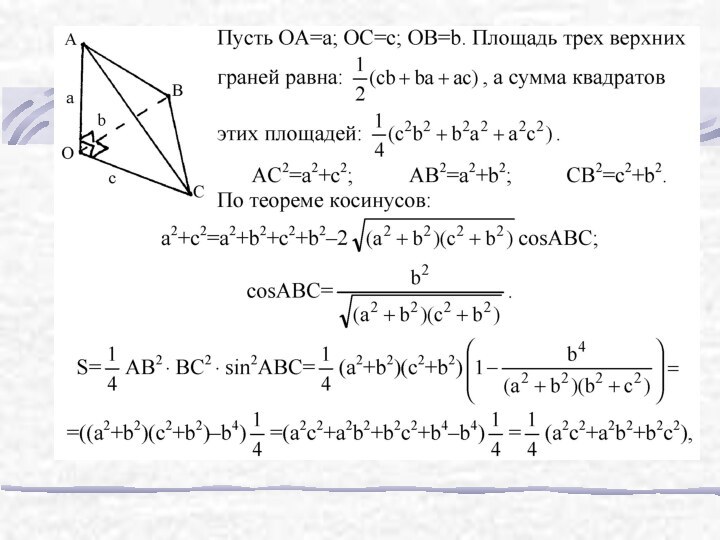
Все плоские углы тетраэдра ОABC при вершине О — прямые. Докажите, что квадрат площади треугольника ABC равен сумме квадратов площадей остальных граней (пространственная теорема Пифагора).






Слайд 4
Три формулировки теоремы Пифагора:
В прямоугольном треугольнике квадрат длины
гипотенузы равен сумме квадратов длин катетов;
Квадрат длины диагонали прямоугольника
равен сумме квадратов длин двух его взаимно перпендикулярных сторон;Квадрат длины любого отрезка равен сумме квадратов длин его проекций на любые две взаимно перпендикулярные прямые.
Слайд 5
С
A
B
BC2=AB2+AC2
(1. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов
Слайд 6 2.Квадрат длины диагонали прямоугольника равен сумме квадратов длин
двух его взаимно перпендикулярных сторон
O
O1
O
O2
A1
A
C
B1
OC2=OA2+OB2OA=O1A1
OB=O2B1
B
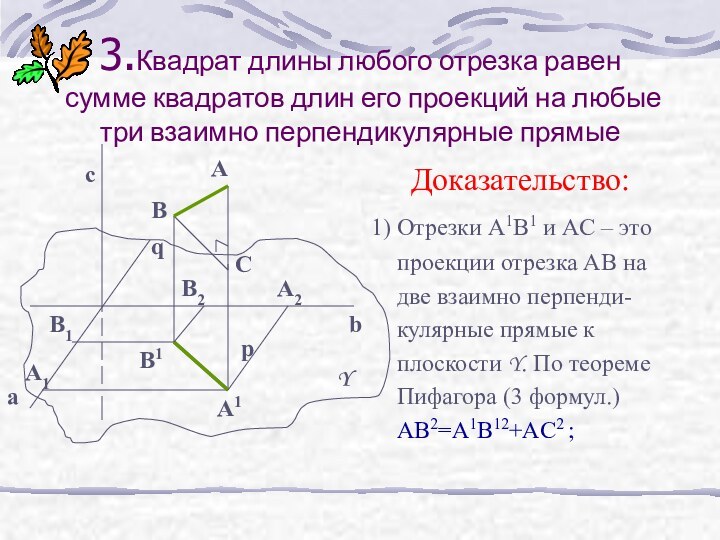
Слайд 7 3.Квадрат длины любого отрезка равен сумме квадратов длин
его проекций на любые три взаимно перпендикулярные прямые
Доказательство: 1) Отрезки A1B1 и AC – это
проекции отрезка АВ на
две взаимно перпенди-
кулярные прямые к
плоскости Y. По теореме
Пифагора (3 формул.)
AB2=A1B12+AC2 ;
b
c
a
p
q
B1
B1
B2
B
A1
A1
A2
A
C
Y
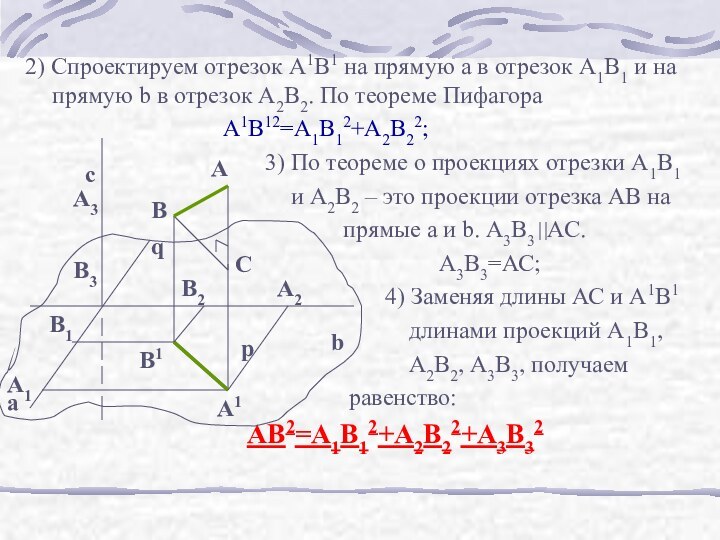
Слайд 8 2) Спроектируем отрезок A1B1 на прямую а в
отрезок А1В1 и на прямую b в отрезок А2В2.
По теореме ПифагораA1B12=A1B12+A2B22;
3) По теореме о проекциях отрезки А1В1
и А2В2 – это проекции отрезка АВ на
прямые a и b. А3В3 АС.
А3В3=АС;
4) Заменяя длины АС и А1В1
длинами проекций А1В1,
А2В2, А3В3, получаем
равенство:
AB2=A1B12+A2B22+A3B32
c
p
q
B1
B1
B2
B
A1
A2
A
C
b
A1
а
B3
A3