стороне
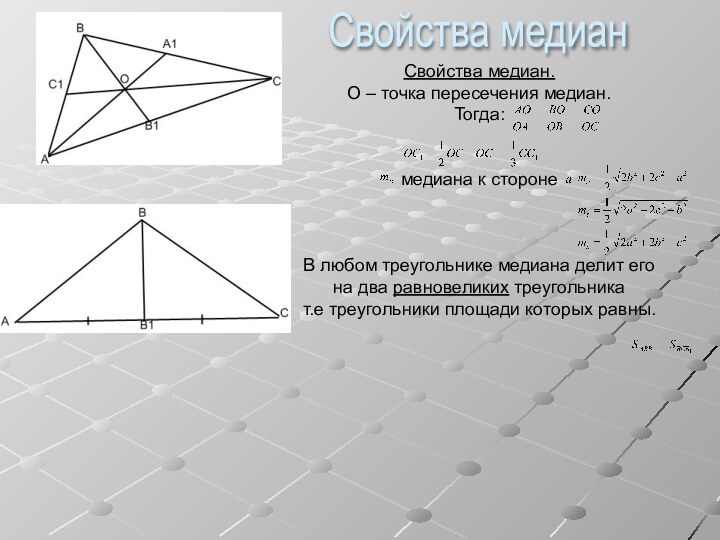
В любом треугольнике медиана делит его
на два равновеликих
треугольникат.е треугольники площади которых равны.
Свойства медиан
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
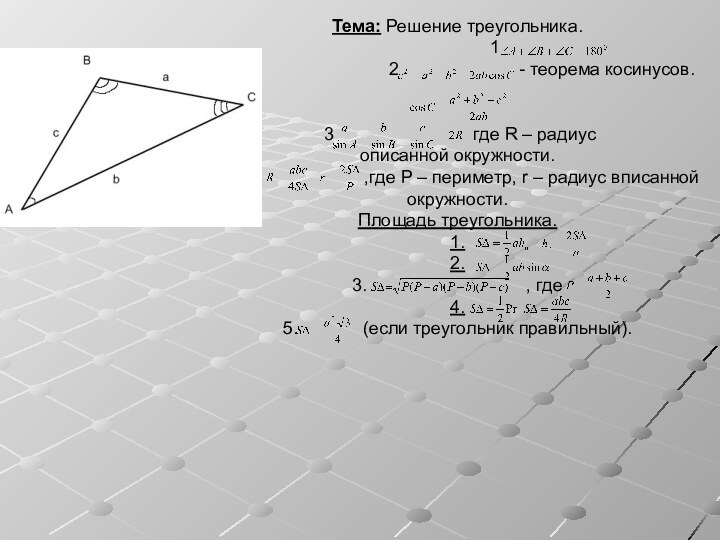

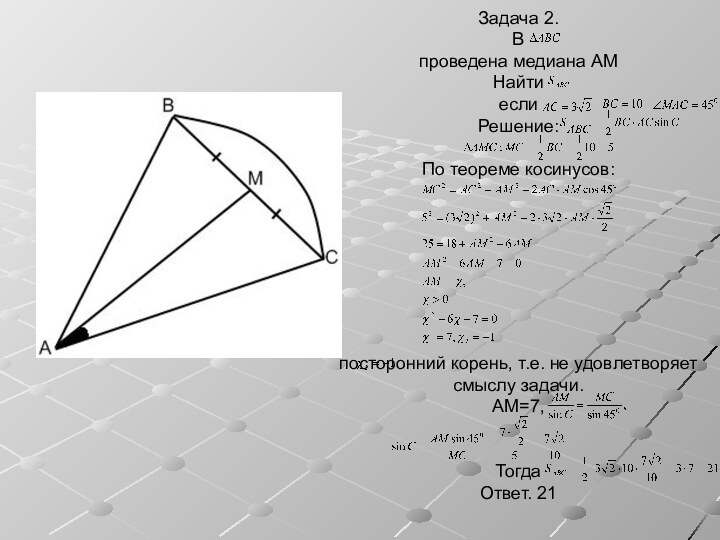
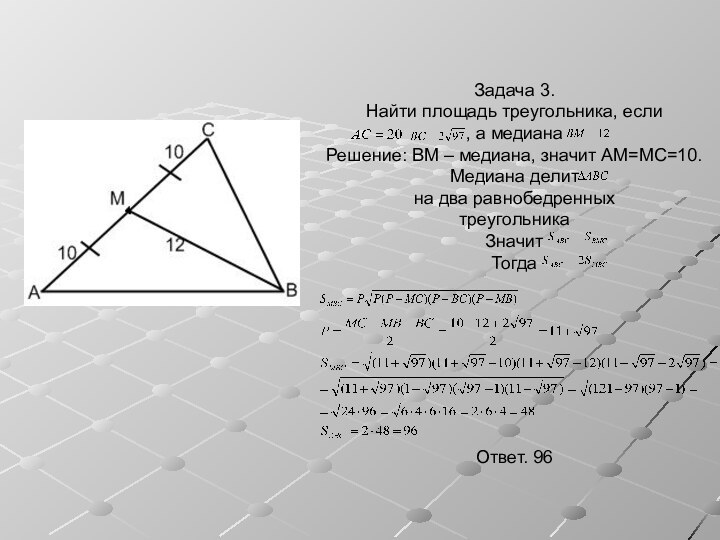
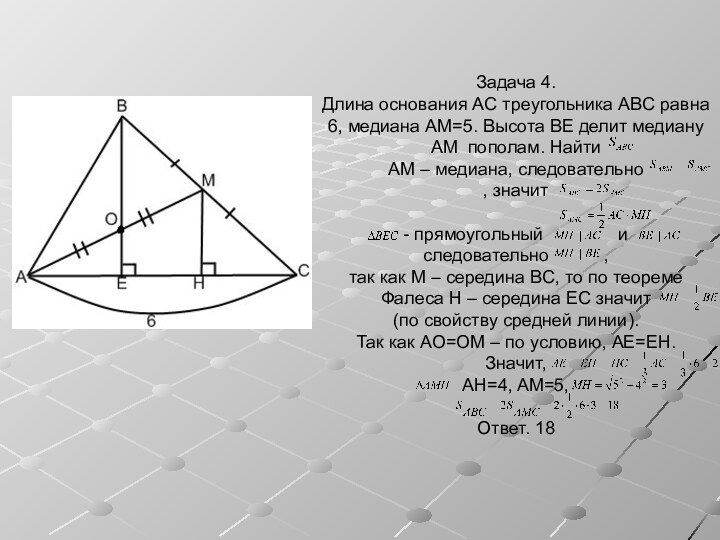

Свойства медиан
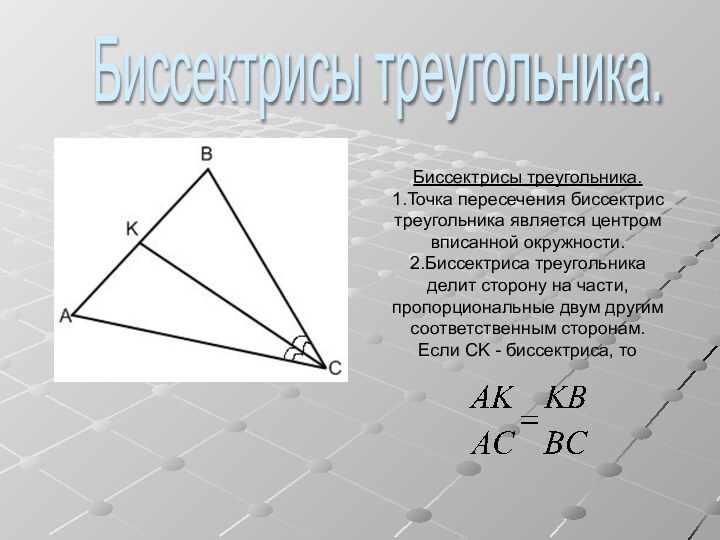
Биссектрисы треугольника.
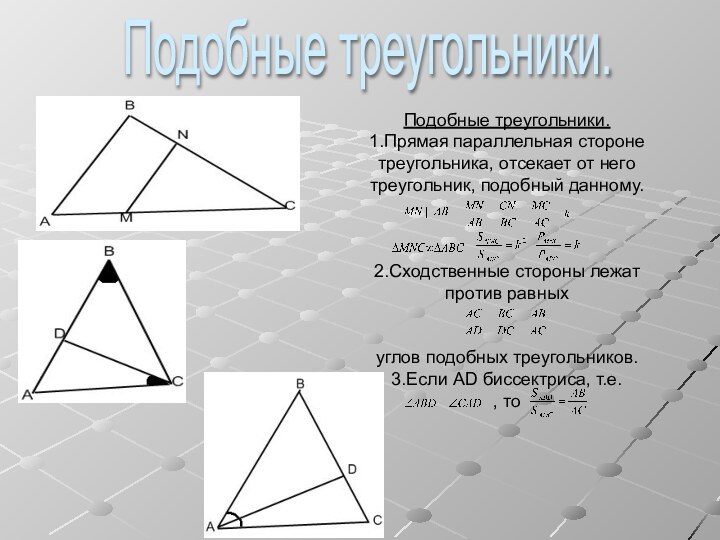
Подобные треугольники.
Задачи!