Вычисление объемов тел с помощью определенного интеграла
5. Объем
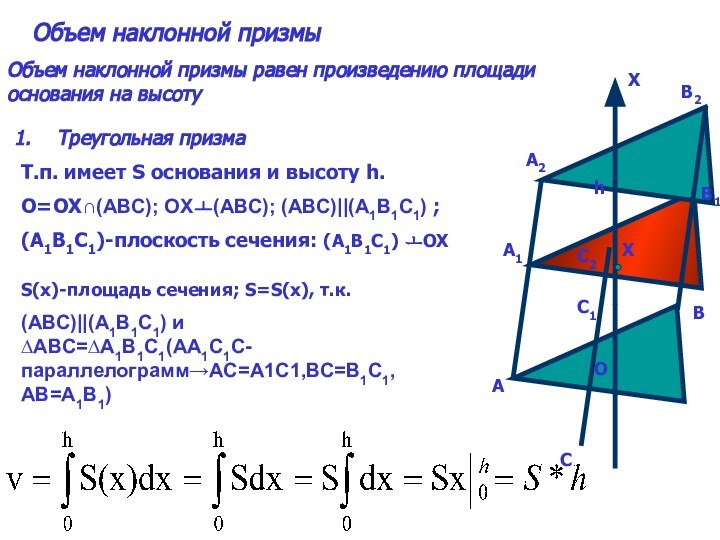
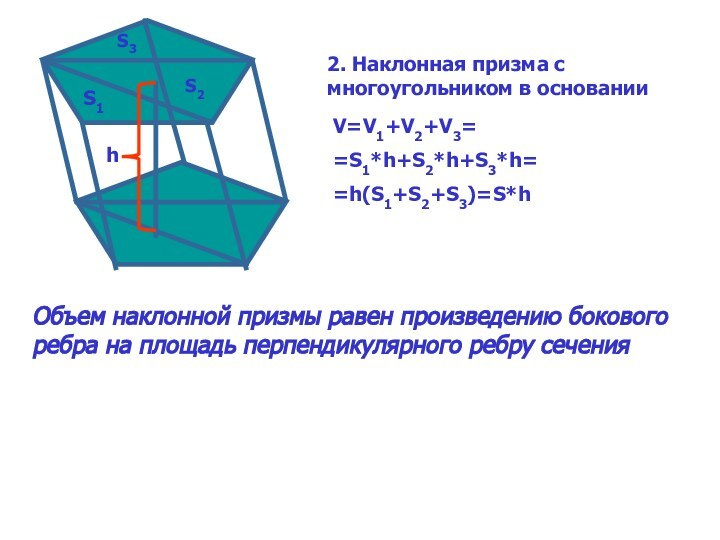
наклонной призмы6. Объем пирамиды
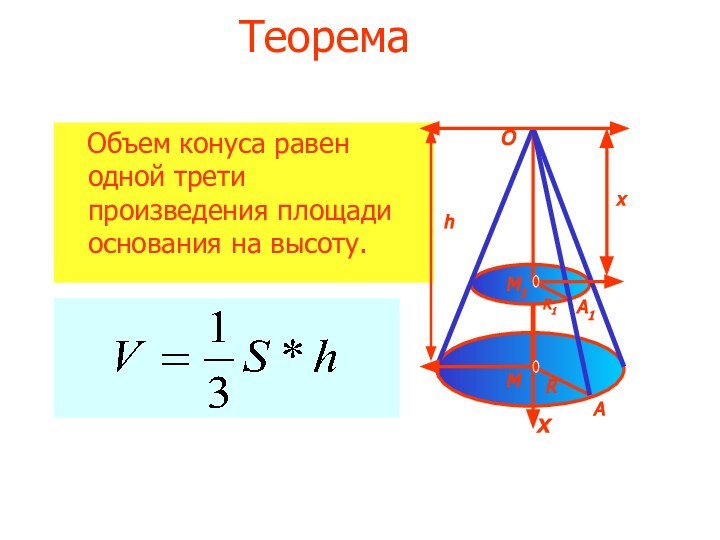
7.Объем конуса
8. Объем шара
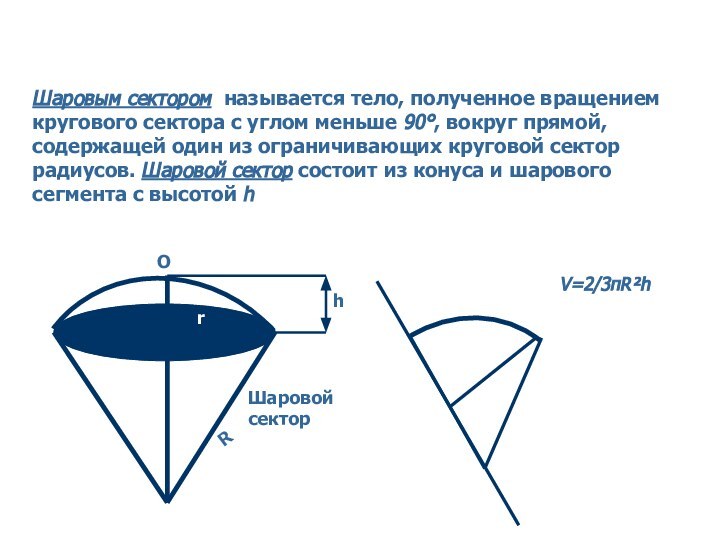
9. Объем шарового сегмента, шарового слоя, шарового сектора
Содержание урока :
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть












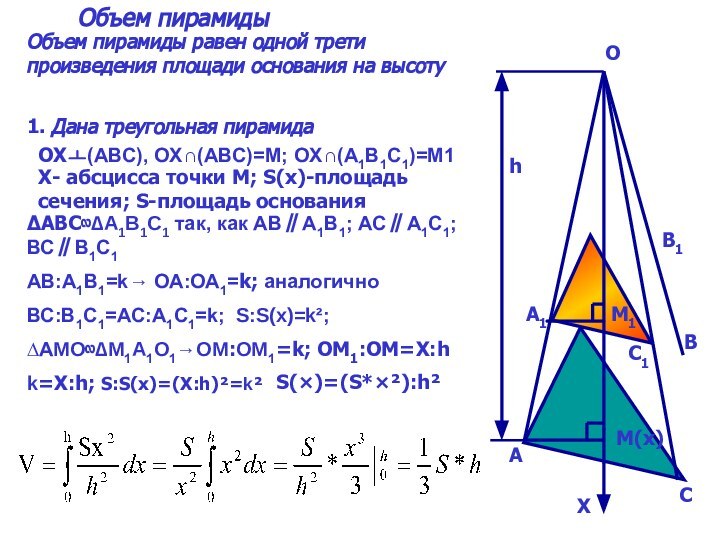


6. Объем пирамиды
7.Объем конуса
8. Объем шара
9. Объем шарового сегмента, шарового слоя, шарового сектора
Содержание урока :
1 см
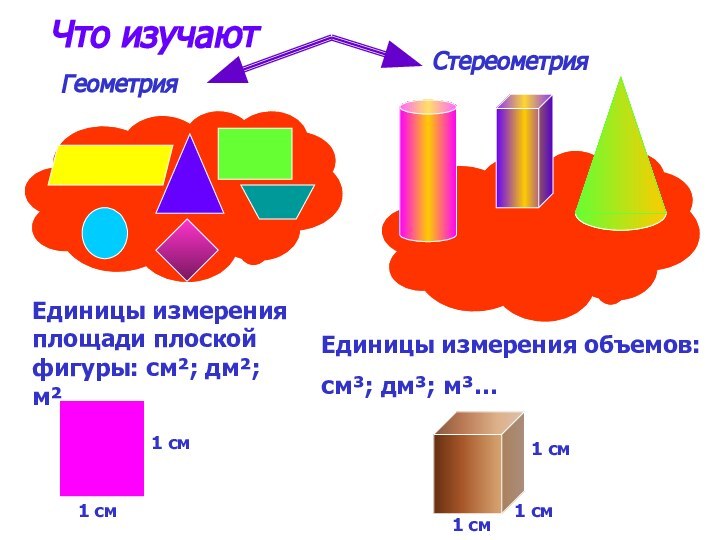
Что изучают
Понятие объема.
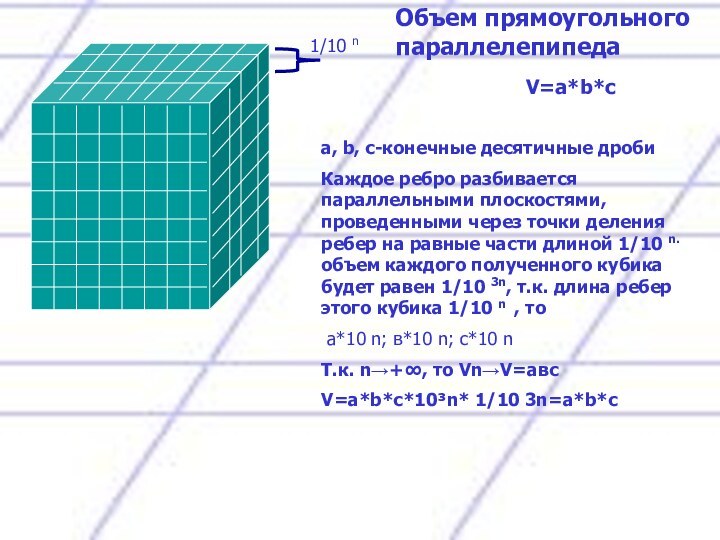
Построим сечение прямоугольного параллелепипеда , проходящее через диагонали верхнего и нижнего оснований
А1
A D B
A1 D1 B1
C1
С
h
r
h
r
Вписанная
призма
Описанная
призма
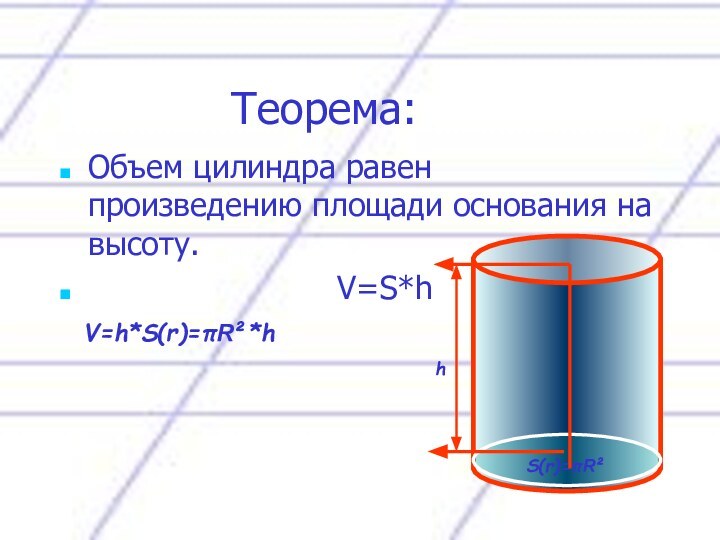
V=h*S(r)=πR²*h
S(r)=πR²
h
Fn=Sn*h где Sn- площадь Цилиндр Цилиндр Призма Fn
основания призмы
Цилиндр Р содержит призму Fn,
которая в свою очередь,
содержит цилиндр Pn.
Тогда Vn< Sn*h
число n =>Rn=r cos 180/n*r
при n → +∞
Поэтому: limVn=V
Из неравенства (1) следует,
что LimSn*h=V
Но LimSn=Пr² таким образом
V=Пr²h
Пr ²=S => V=Sh
P
Pn
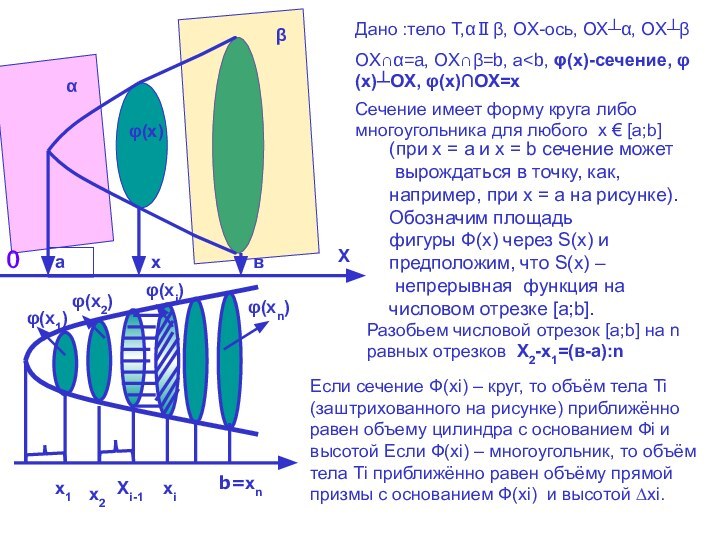
(при х = а и х = b сечение может
вырождаться в точку, как,
например, при х = а на рисунке). Обозначим площадь
фигуры Ф(х) через S(х) и
предположим, что S(х) –
непрерывная функция на
числовом отрезке [a;b].
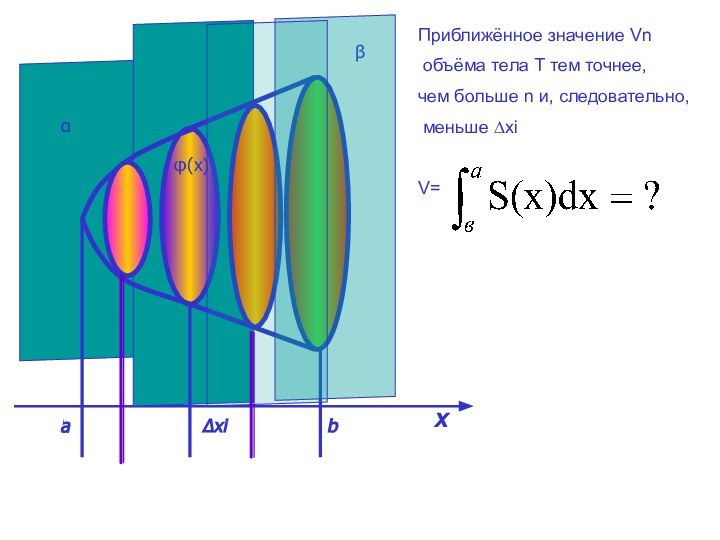
Разобьем числовой отрезок [a;b] на n равных отрезков Х2-х1=(в-а):n
Если сечение Ф(хi) – круг, то объём тела Ti (заштрихованного на рисунке) приближённо равен объему цилиндра с основанием Фi и высотой Если Ф(хi) – многоугольник, то объём тела Тi приближённо равен объёму прямой призмы с основанием Ф(xi) и высотой ∆xi.
φ(x1)
φ(x2)
φ(xi)
φ(xn)
х1
х2
хi
b=хn
Хi-1
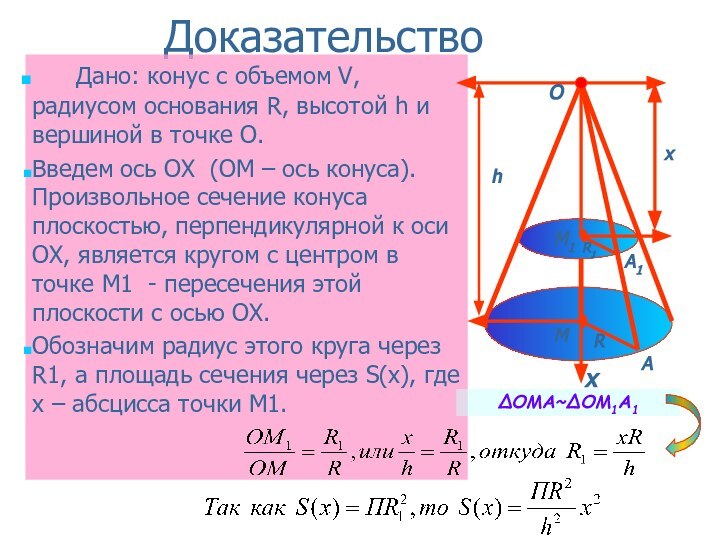
S(x)-площадь сечения; S=S(x), т.к.
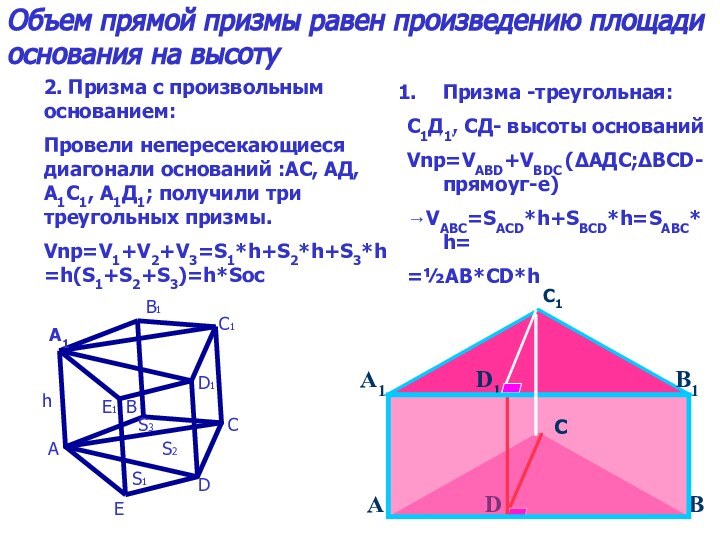
(АВС)||(А1В1С1) и ∆ABC=∆A1B1C1(АА1С1С-параллелограмм→АС=А1С1,ВС=В1С1, АВ=А1В1)
∆ABC∾∆A1B1C1 так, как АВ∥А1В1; АС∥А1С1; ВС∥В1С1
АВ:А1В1=k→ ОА:ОА1=k; аналогично
ВС:В1С1=АС:А1С1=k; S:S(x)=k²;
∆AMO∾∆M1A1O1→OM:OM1=k; ОМ1:ОМ=Х:h
k=Х:h; S:S(x)=(Х:h)²=k²
S(×)=(S*ײ):h²
α
α1
φ
φ1
М
М1
O
h
х
х
A
A1
М
М1
R
R1
O
ΔОМА~ΔОМ1А1
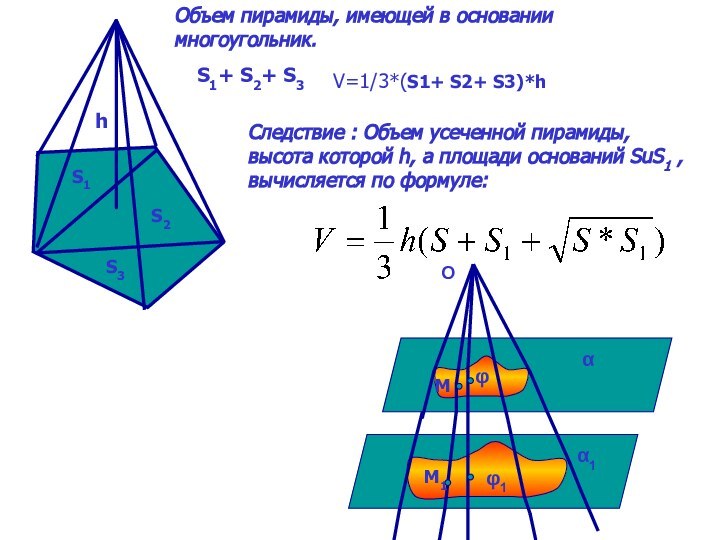
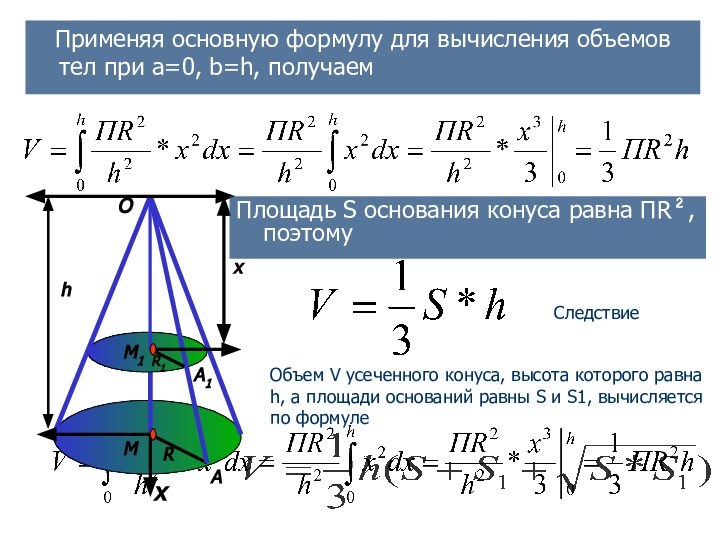
Следствие
Объем V усеченного конуса, высота которого равна h, а площади оснований равны S и S1, вычисляется по формуле
Найти : V
S (x)=πr²
S (x)=π(R²-x²)
-R≤ x ≤R
Применяя основную формулу для вычисления объемов имеем :а =-R; b=R
r
R
К
Vш. с . =πh²(R-1/3h)
OX ᅩ ⍶
S (x)=πх², где R-h ≤x ≤R
где S (x)- площадь сечения
V=π∫(R²-x²)dx=π(R²x-x³/3)| =πh²(R-1/3h)
R
R-h
R-h
R
По определению правила вычислению объемов a=R-h; b=R
S (x)- непрерывная функция на [a; b]
h
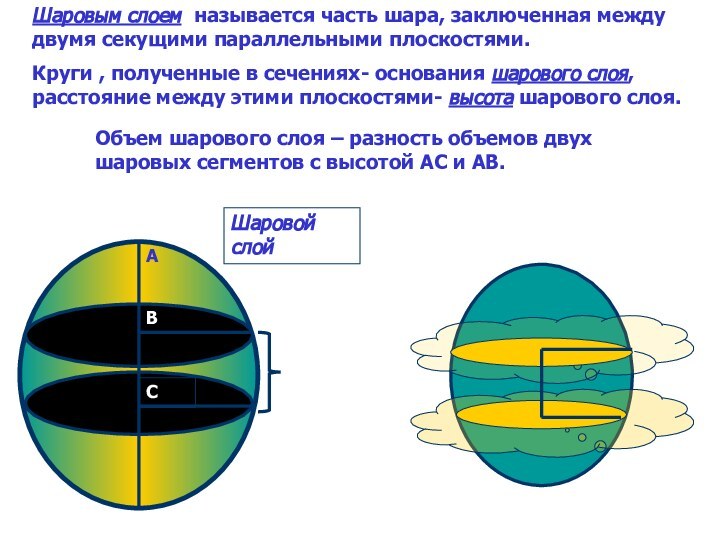
Объем шарового слоя – разность объемов двух шаровых сегментов с высотой АС и АВ.