- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Свойства призмы
Содержание
- 2. Сколько ребер может иметь выпуклый многогранник? Почему не может быть 7 ребер?
- 3. Рассмотрим F⊂α и не принадлежащую прямой а.
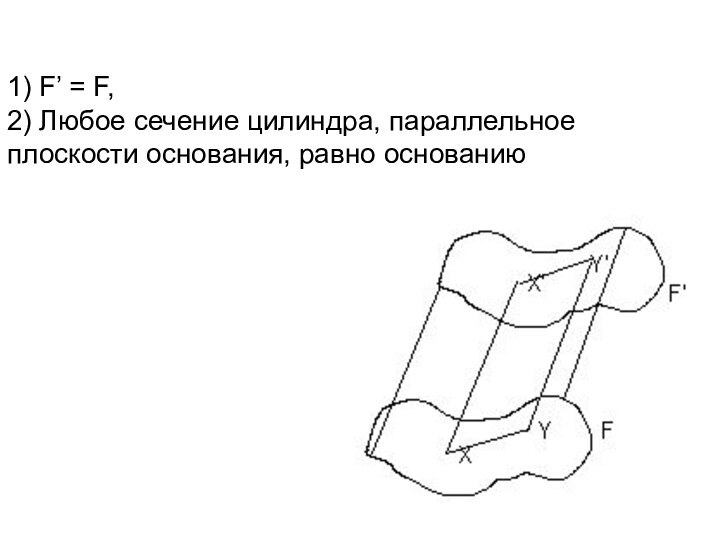
- 4. 1) F’ = F, 2) Любое сечение цилиндра, параллельное плоскости основания, равно основанию
- 5. Определения. Высотой цилиндра называется общий перпендикуляр к
- 6. Цилиндр, основанием которой является многоугольник, называется призмой.Ребра,
- 7. Какие свойства призмы следуют из свойств цилиндра?
- 8. Призмой называется многогранник, у которого две грани,
- 9. Сформулируйте и обоснуйте Н. и Д. условие
- 10. Вокруг каких из разновидностей призм всегда можно описать сферу? Прямая треугольная; правильная.
- 11. Верно ли, что в любую правильную призму
- 12. Существую ли наклонные призмы, в которые можно вписать сферу?
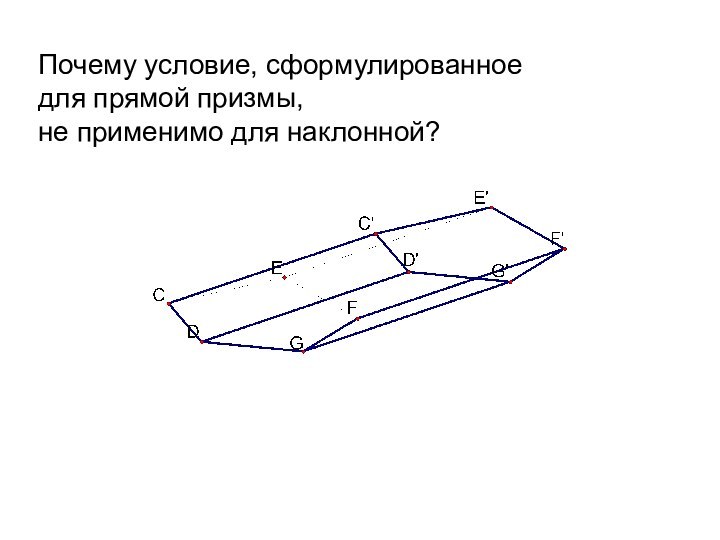
- 13. Почему условие, сформулированное для прямой призмы, не применимо для наклонной?
- 14. Существует ли треугольная призма, у которой: а)
- 15. Каждое ребро треугольной призмы АВСA’B’C’ имеет длину
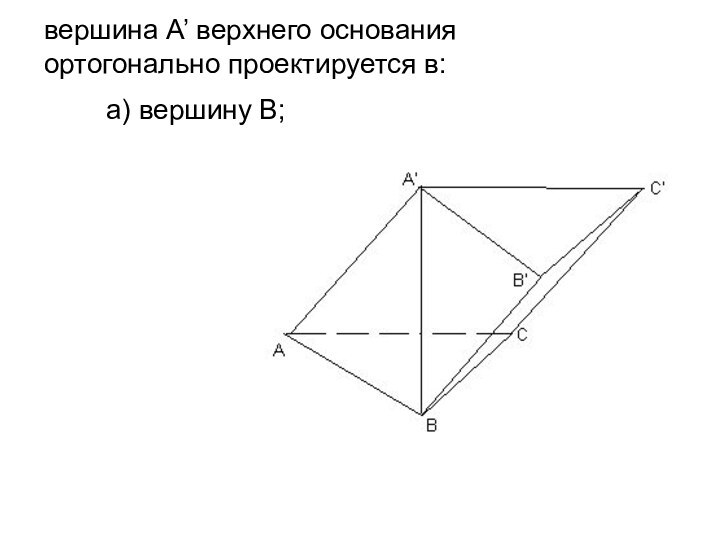
- 16. а) вершину В;вершина А’ верхнего основания ортогонально проектируется в:
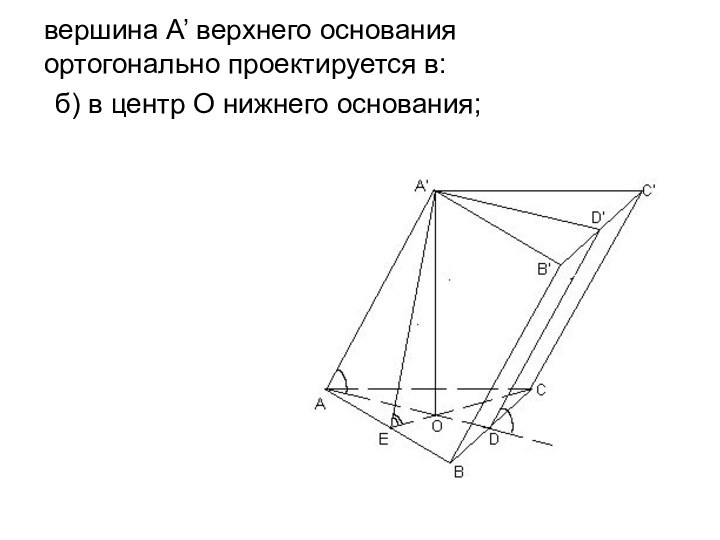
- 17. б) в центр О нижнего основания;вершина А’ верхнего основания ортогонально проектируется в:
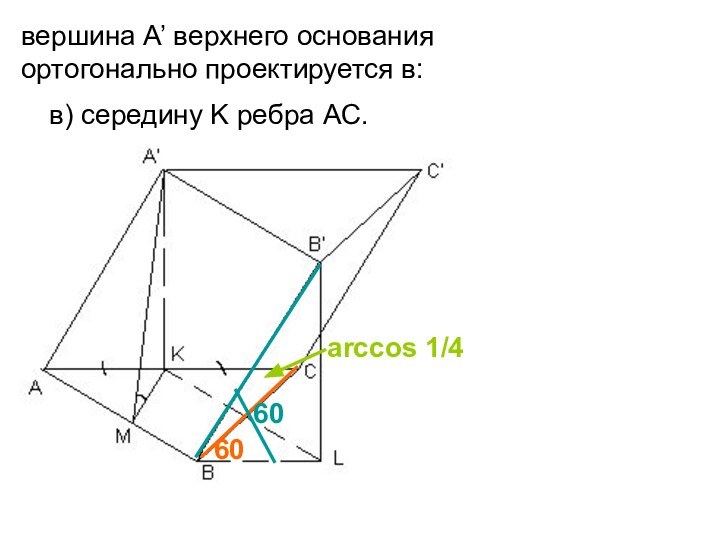
- 18. в) середину K ребра АС. вершина А’ верхнего основания ортогонально проектируется в:6060arccos 1/4
- 19. c – проекция наклонной а на
- 20. Теорема косинусов для трехгранного углатогда cosγ =
- 21. Скачать презентацию
- 22. Похожие презентации
Сколько ребер может иметь выпуклый многогранник? Почему не может быть 7 ребер?











Слайд 3
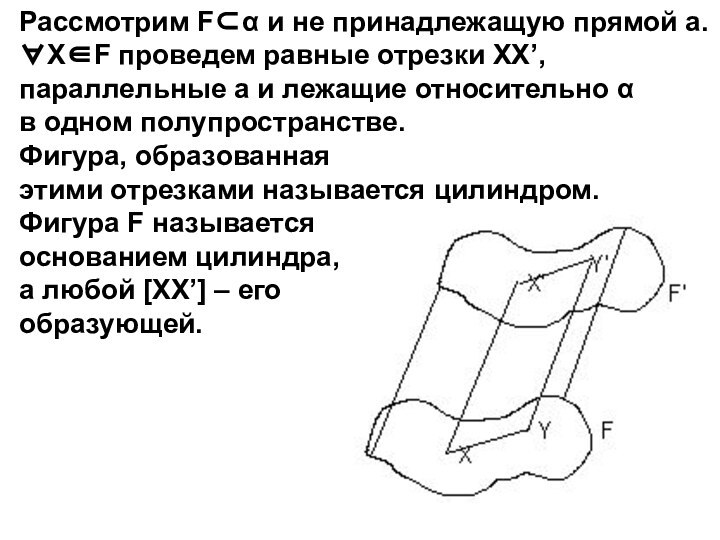
Рассмотрим F⊂α и не принадлежащую прямой а.
∀X∈F
проведем равные отрезки XX’,
параллельные а и лежащие относительно
α в одном полупространстве.
Фигура, образованная
этими отрезками называется цилиндром.
Фигура F называется
основанием цилиндра,
а любой [XX’] – его
образующей.
Слайд 5
Определения.
Высотой цилиндра называется общий
перпендикуляр к плоскостям
его оснований.
2) Высотой цилиндра называется расстояние
между его
основаниями.
Слайд 6
Цилиндр, основанием которой
является многоугольник,
называется призмой.
Ребра, не
лежащие в плоскостях оснований;
грани, не являющиеся основаниями;
общий
перпендикуляр к основаниям, заключенный между их плоскостями
(расстояние между плоскостями оснований)
Сформулируйте определения боковых ребер
и боковых граней призмы; высоты призмы
Слайд 7
Какие свойства призмы следуют из свойств цилиндра?
Равенство
сечений призмы,
параллельных основанию,
в частности, равенство оснований призмы;
равенство и параллельность боковых ребер
и высот призмы;
боковые грани – параллелограммы
Слайд 8
Призмой называется многогранник,
у которого две грани, называемые
основаниями,
равны и их соответственные стороны
параллельны,
а остальные
грани – параллелограммы, у каждого из которых две стороны являются
соответственными основаниями
параллелограммов
Докажите, что это определение эквивалентно
предыдущему.
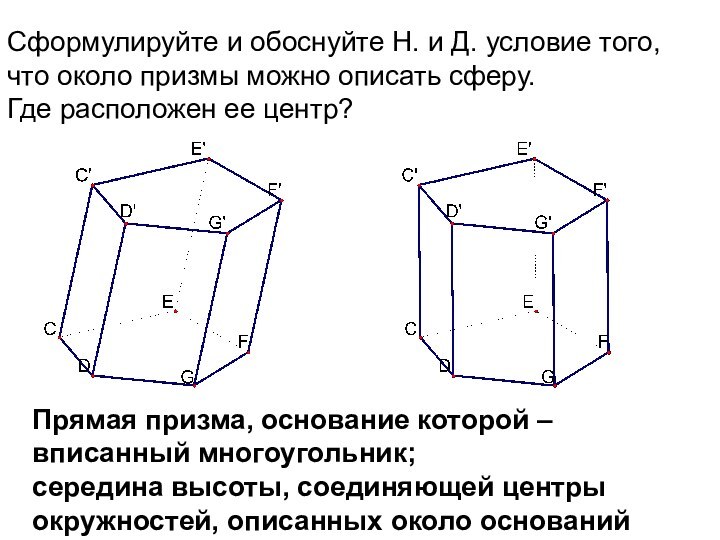
Слайд 9 Сформулируйте и обоснуйте Н. и Д. условие того,
что около призмы можно описать сферу.
Где расположен ее
центр? Прямая призма, основание которой –
вписанный многоугольник;
середина высоты, соединяющей центры
окружностей, описанных около оснований
Слайд 10
Вокруг каких из разновидностей призм
всегда можно описать
сферу?
Прямая треугольная; правильная.
Слайд 11
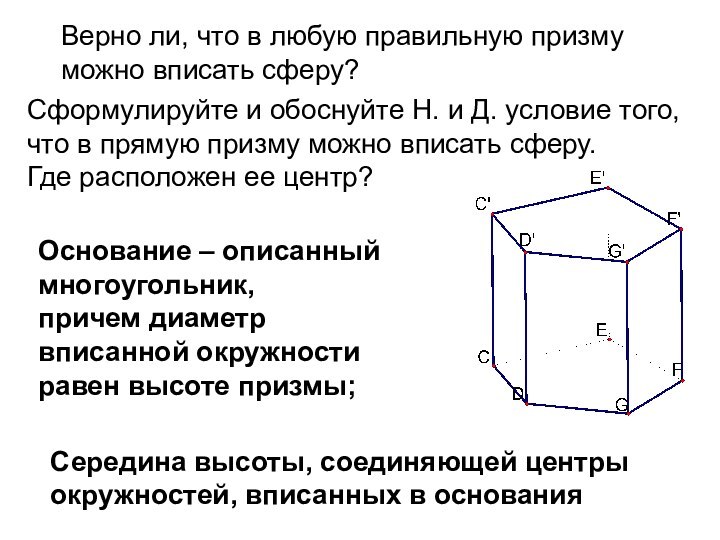
Верно ли, что в любую правильную призму
можно
вписать сферу?
Сформулируйте и обоснуйте Н. и Д. условие
того, что в прямую призму можно вписать сферу.
Где расположен ее центр?
Середина высоты, соединяющей центры
окружностей, вписанных в основания
Основание – описанный многоугольник,
причем диаметр вписанной окружности
равен высоте призмы;
Слайд 14
Существует ли треугольная призма, у которой:
а) ровно
одна боковая грань — прямоугольник;
б) ровно две боковые
грани — прямоугольники; в) ровно одна грань перпендикулярна основанию;
г) ровно две грани перпендикулярны основанию;
д) боковое ребро перпендикулярно ровно одной
стороне основания;
е) центр вписанной сферы не совпадает
с центром описанной сферы?
Слайд 15
Каждое ребро треугольной призмы АВСA’B’C’
имеет длину а.
Найдите углы наклона боковых ребер
и граней к плоскости
основания, если вершина А’ верхнего основания
ортогонально проектируется в:
а) вершину В;
б) в центр О нижнего основания;
в) середину K ребра АС.
Слайд 18
в) середину K ребра АС.
вершина А’ верхнего
основания
ортогонально проектируется в:
60
60
arccos 1/4
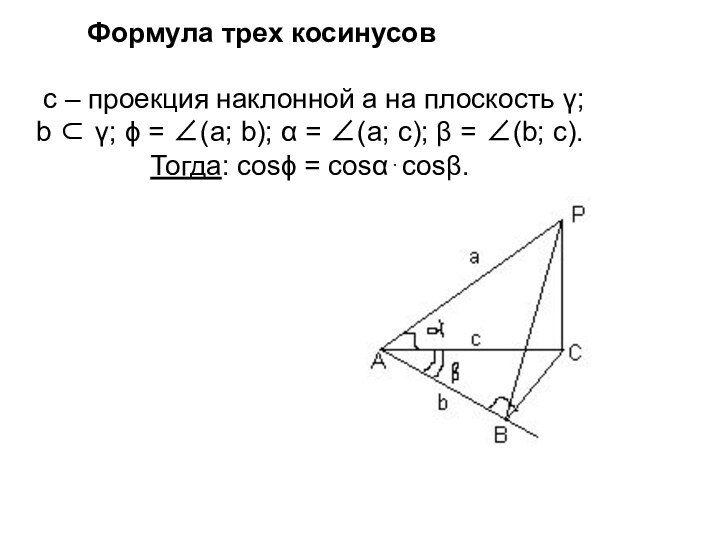
Слайд 19 c – проекция наклонной а на плоскость
γ;
b ⊂ γ; ϕ = ∠(a; b); α
= ∠(a; c); β = ∠(b; c). Тогда: cosϕ = cosα⋅cosβ.
Формула трех косинусов
Слайд 20
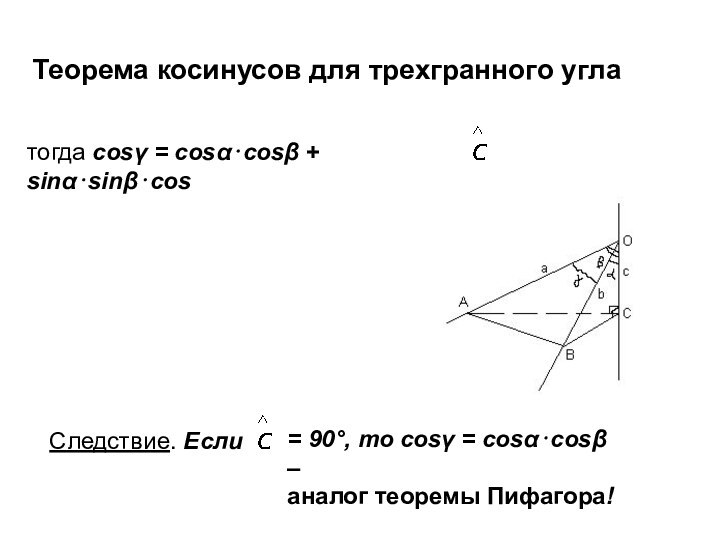
Теорема косинусов для трехгранного угла
тогда cosγ = cosα⋅cosβ
+ sinα⋅sinβ⋅cos
Следствие. Если
= 90°, то cosγ = cosα⋅cosβ
– аналог теоремы Пифагора!





























