- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение сечений многогранников
Содержание
- 2. Работа выполнена ученицей 10 А класса
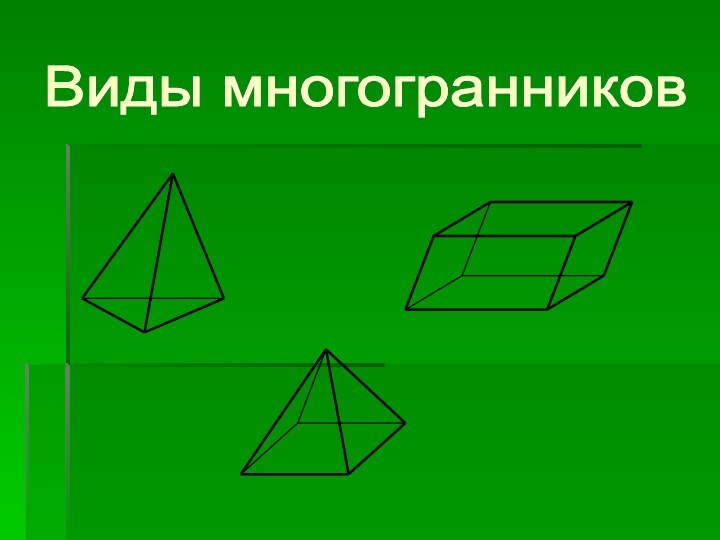
- 3. Виды многогранников
- 4. Тетраэдр
- 5. Параллелепипед
- 6. Пирамида
- 7. АВаАВСЧерез две точки А и В можно
- 8. Если две точки прямой принадлежат плоскости, то
- 9. Задачу построения сечения многогранников рассмотрим на примерах:
- 10. Дан параллелепипед
- 11. Сечение проходит через точку О и прямую
- 12. Дан тетраэдр KLMNТочка А середина ребра MN.КМLNА
- 13. Т.к прямая и точка вне ее однозначно
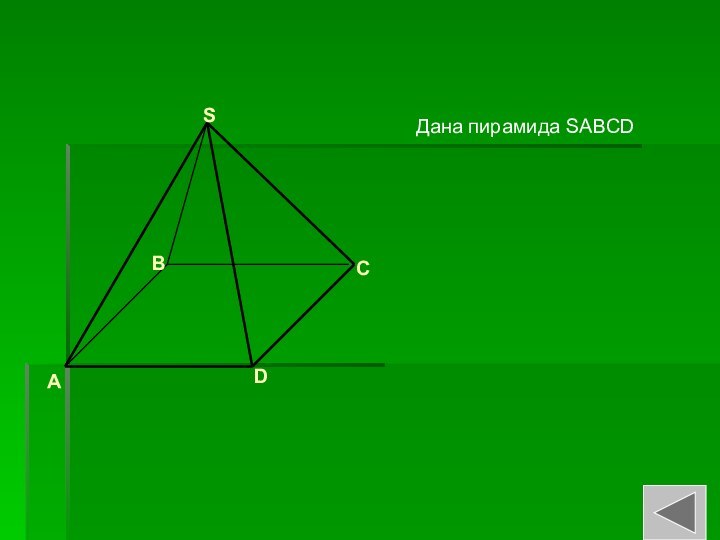
- 14. Дана пирамида SABCDABCDS
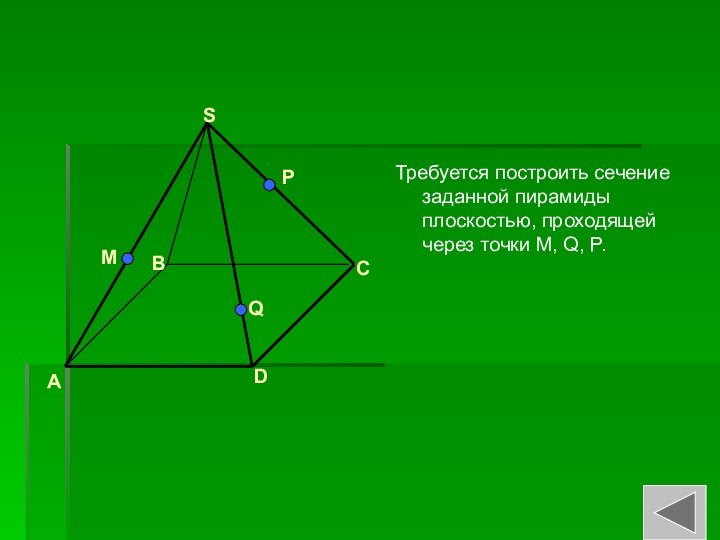
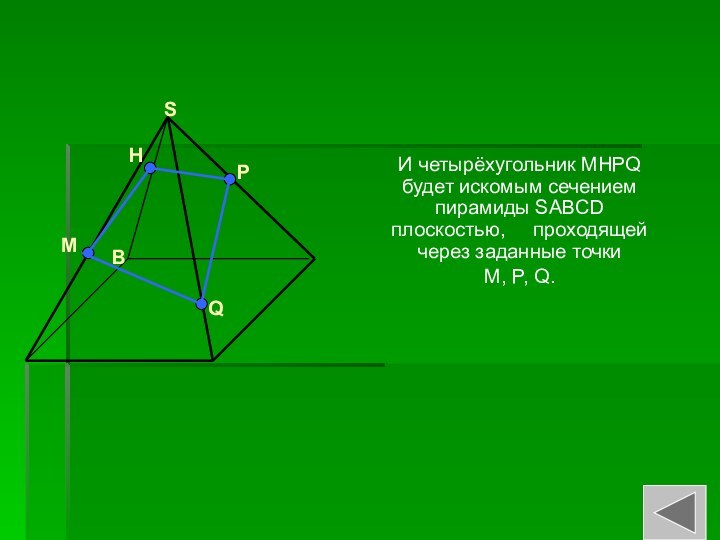
- 15. Требуется построить сечение заданной пирамиды плоскостью, проходящей через точки M, Q, P.ABCDSMQP
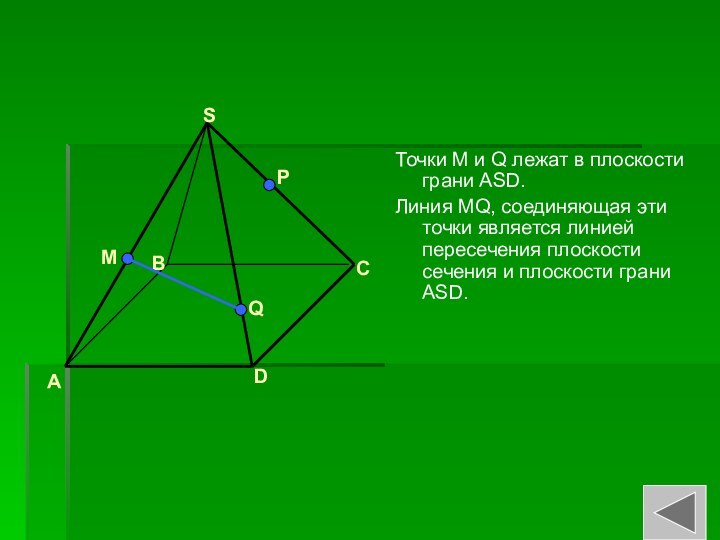
- 16. Точки M и Q лежат в плоскости
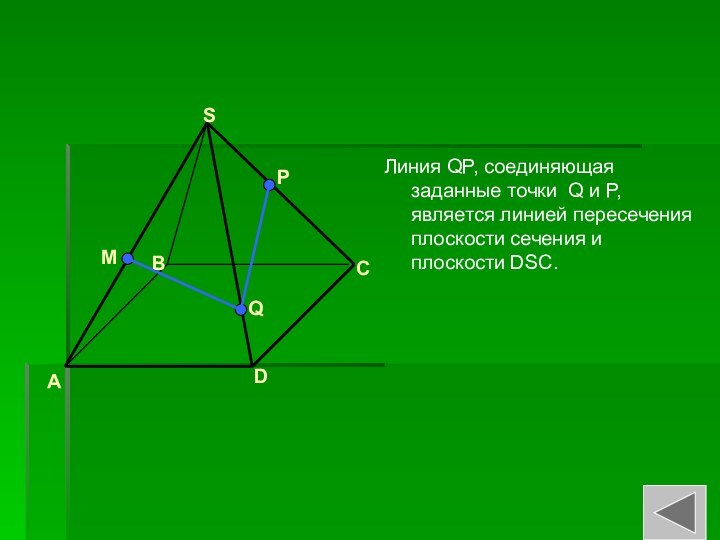
- 17. Линия QP, соединяющая заданные точки Q и P, является линией пересечения плоскости сечения и плоскости DSC.ABCDSMQP
- 18. Линии MQ и AD лежат в одной
- 19. Линии PQ и CD лежат в одной
- 20. Точки Е и F принадлежат плоскости сечения
- 21. Линии EF и BC лежат в одной
- 22. Точки P и G принадлежат
- 23. Линией пересечения плоскости
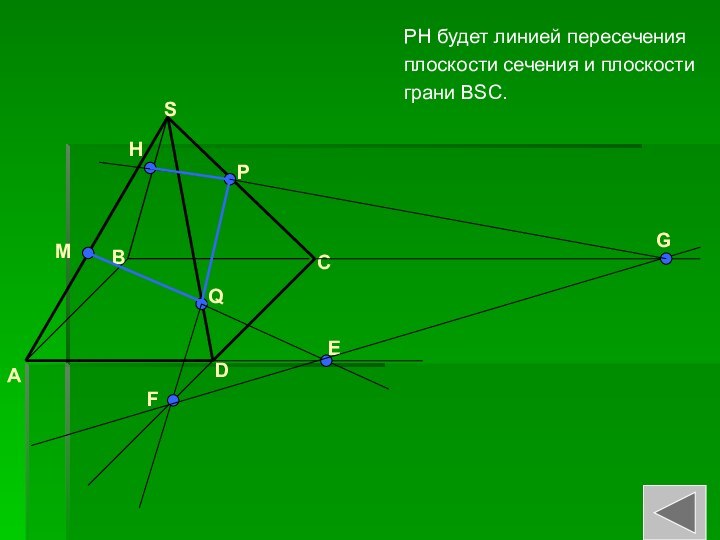
- 24. PH будет линией пересечения плоскости сечения и плоскости грани BSC.ABCDSMQPЕFGН
- 25. Ну и наконец,
- 26. Скачать презентацию
- 27. Похожие презентации











Слайд 2 Работа выполнена ученицей 10 А класса МОУ СОШ №7 Кудряшовой
Ксенией
школы № 7 Дорофеева Оксана Викторовна
Слайд 7
А
В
а
А
В
С
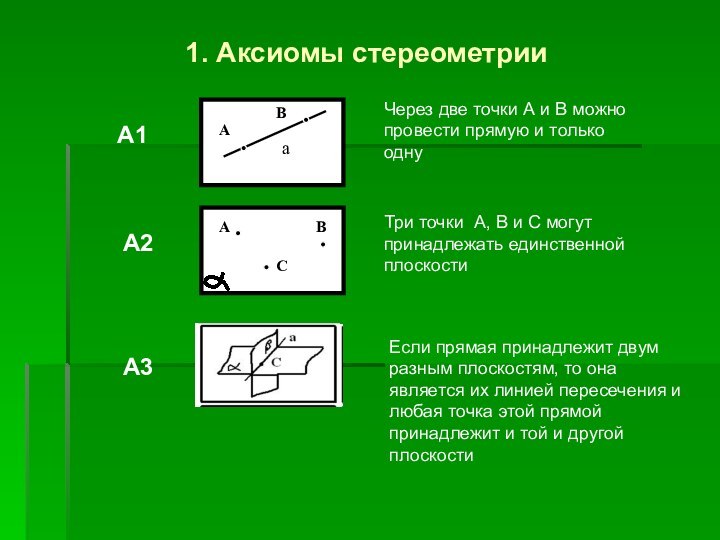
Через две точки А и В можно провести
прямую и только одну
Три точки А, В и С
могут принадлежать единственной плоскостиЕсли прямая принадлежит двум разным плоскостям, то она является их линией пересечения и любая точка этой прямой принадлежит и той и другой плоскости
А1
А2
А3
1. Аксиомы стереометрии
Слайд 8
Если две точки прямой принадлежат
плоскости, то и
вся прямая принадлежит
плоскости.
Через прямую и не лежащую на
ней точку можно провести плоскость
и при том только одну.
Через две пересекающиеся прямые
можно провести плоскость и при
том только одну.
2. Следствия из аксиом стереометрии
Сл.1
Сл.2
Сл.3
Слайд 9
Задачу построения сечения многогранников рассмотрим на примерах:
1.Построить сечение
параллелепипеда ABCDA1B1C1D1 , проходящее через ребро СС1 и
точку пересечения диагоналей грани АА1DD1.2.Построить сечение тетраэдра KLMN плоскостью, проходящей через ребро KL и середину А ребра MN.
3.Построить сечение пирамиды плоскостью, проходящей через три заданные точки.
Слайд 10
Дан параллелепипед
АВСD A1 B1 C1 D1
Точка
О – середина диагоналей грани АА1 D1DA
A
B
C
D
A1
B1
C1
D1
О
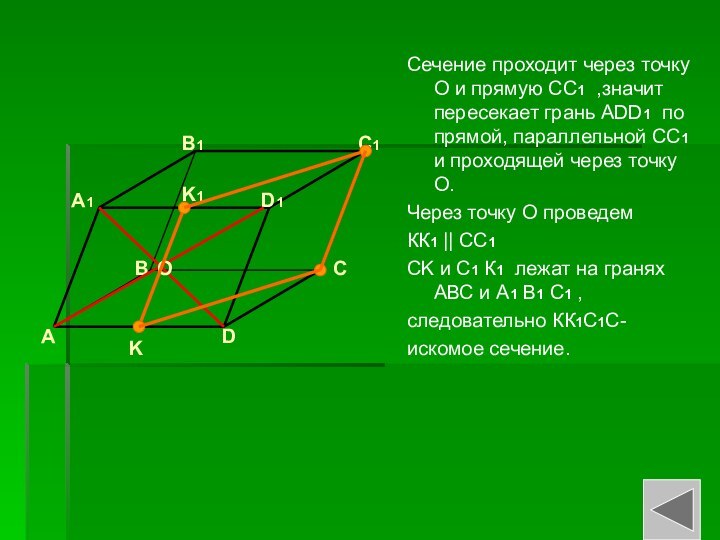
Слайд 11 Сечение проходит через точку О и прямую СС1
,значит пересекает грань ADD1 по прямой, параллельной СС1 и
проходящей через точку О.Через точку О проведем
КК1 || CC1
CK и С1 К1 лежат на гранях АВС и А1 В1 С1 ,
следовательно КК1С1С-
искомое сечение.
A
B
C
D
A1
B1
C1
D1
О
K
K1
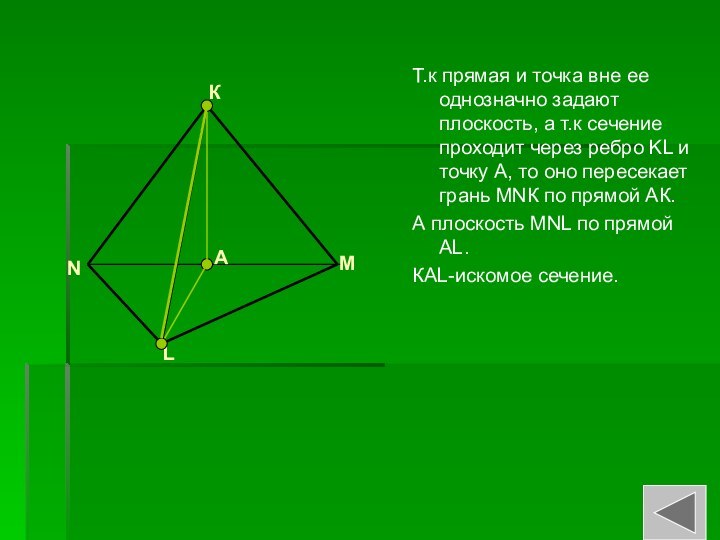
Слайд 13 Т.к прямая и точка вне ее однозначно задают
плоскость, а т.к сечение проходит через ребро KL и
точку А, то оно пересекает грань MNК по прямой АК.А плоскость MNL по прямой AL.
КАL-искомое сечение.
К
М
L
N
А
Слайд 15 Требуется построить сечение заданной пирамиды плоскостью, проходящей через
точки M, Q, P.
A
B
C
D
S
M
Q
P
Слайд 16 Точки M и Q лежат в плоскости грани
ASD.
Линия MQ, соединяющая эти точки является линией пересечения плоскости
сечения и плоскости грани ASD.A
B
C
D
S
M
Q
P
Слайд 17 Линия QP, соединяющая заданные точки Q и P,
является линией пересечения плоскости сечения и плоскости DSC.
A
B
C
D
S
M
Q
P
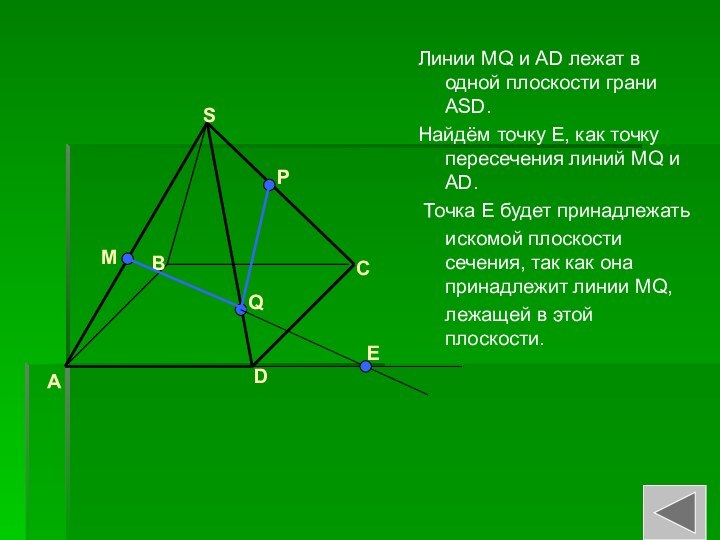
Слайд 18 Линии MQ и AD лежат в одной плоскости
грани ASD.
Найдём точку Е, как точку пересечения линий
MQ и AD. Точка Е будет принадлежать
искомой плоскости сечения, так как она принадлежит линии MQ,
лежащей в этой плоскости.
A
B
C
D
S
M
Q
P
Е
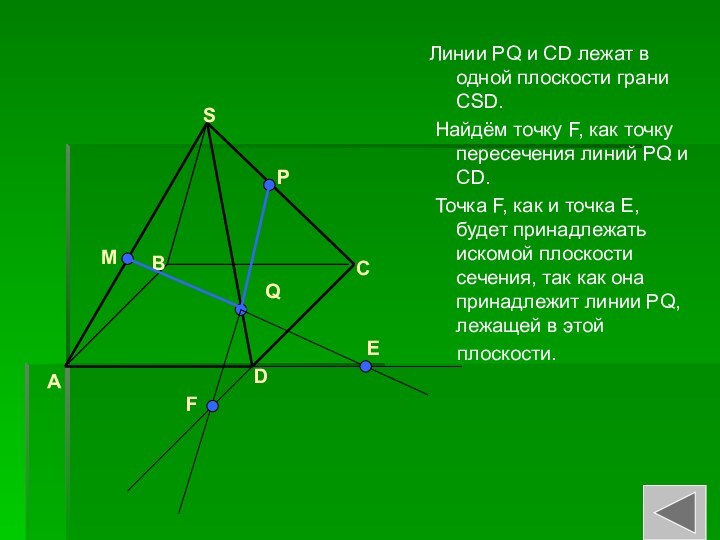
Слайд 19 Линии PQ и CD лежат в одной плоскости
грани CSD.
Найдём точку F, как точку пересечения линий
PQ и CD. Точка F, как и точка Е, будет принадлежать искомой плоскости сечения, так как она принадлежит линии PQ, лежащей в этой
плоскости.
A
B
C
D
S
M
Q
P
Е
F
Слайд 20
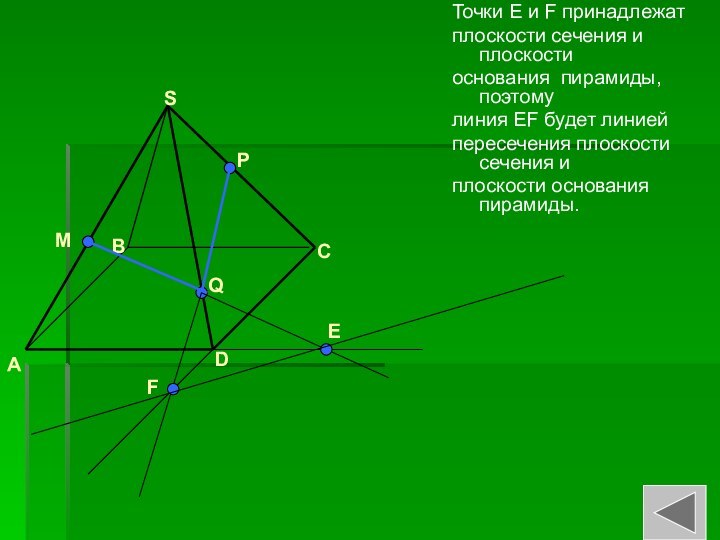
Точки Е и F принадлежат
плоскости сечения и
плоскости
основания пирамиды, поэтому
линия EF будет линией
пересечения
плоскости сечения иплоскости основания пирамиды.
A
B
C
D
S
M
Q
P
Е
F
Слайд 21 Линии EF и BC лежат в одной плоскости
основания пирамиды ABCD.
Найдём точку G, как точку
пересечения линий EF и BC. A
B
C
D
S
M
Q
P
Е
F
G
Точка G будет принадлежать искомой плоскости сечения, так
как она принадлежит линии EF, лежащей в этой плоскости.
Слайд 22
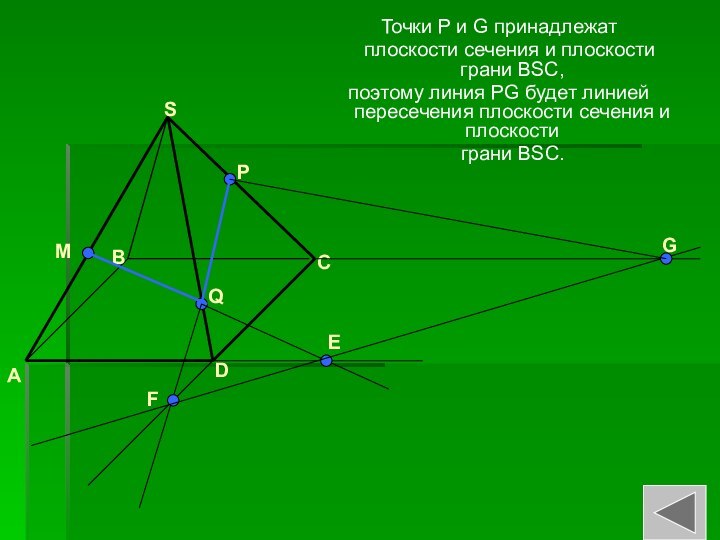
Точки P и G принадлежат
плоскости
сечения и плоскости грани BSC,
поэтому линия PG будет
линией пересечения плоскости сечения и плоскости грани BSC.
A
B
C
D
S
M
Q
P
Е
F
G
Слайд 23
Линией пересечения плоскости
сечения и плоскости грани BSC
будет линия , являющаясяпродолжением PG, которая пересечет ребро BS пирамиды в точке H.
A
B
C
D
S
M
Q
P
Е
F
G
Н
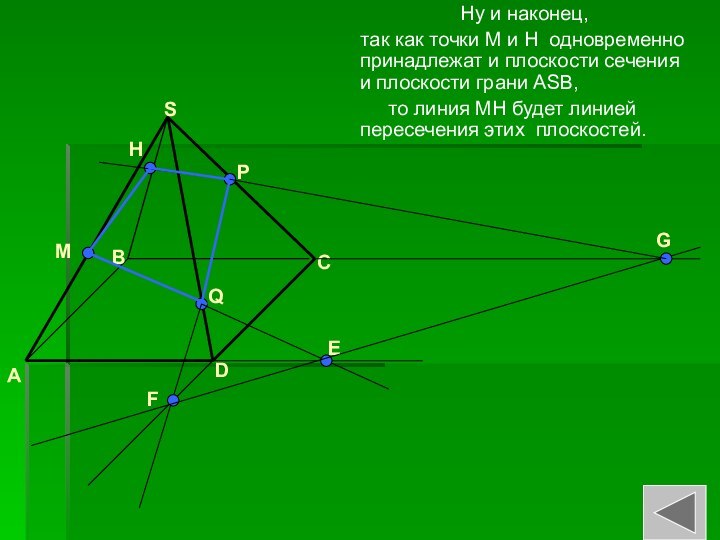
Слайд 25
Ну и наконец,
так
как точки M и H одновременно принадлежат и плоскости
сечения и плоскости грани ASB,то линия MH будет линией пересечения этих плоскостей.
A
B
C
D
S
M
Q
P
Е
F
G
Н