- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
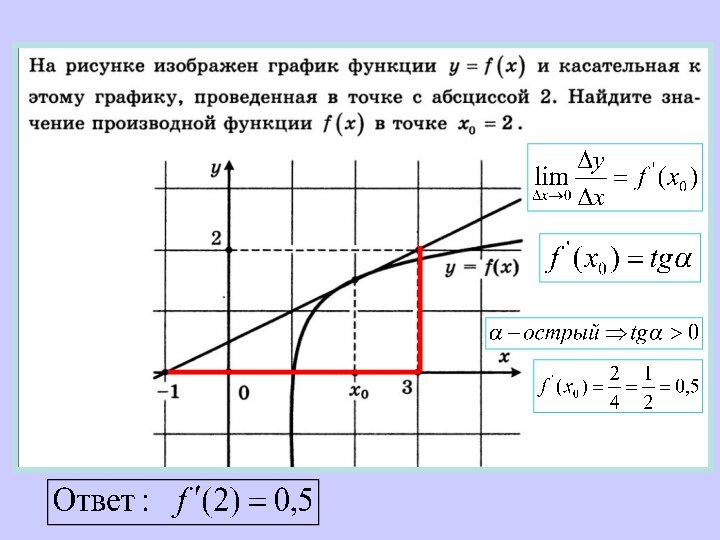
Презентация на тему Уравнение касательной к графику функции
Содержание
- 2. Верно ли определение?Касательная – это прямая, имеющая с данной кривой одну общую точку.
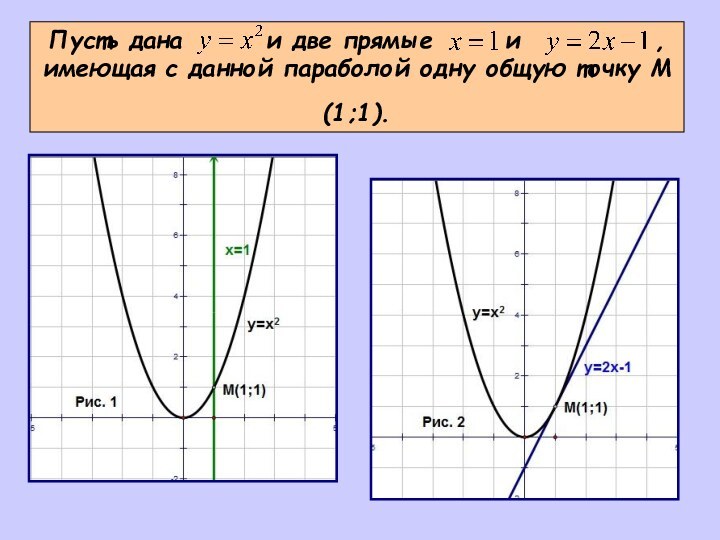
- 3. Пусть дана и две
- 4. На данном уроке:выясним, что же такое касательная
- 5. Определение производнойПусть функция
- 6. Правила дифференцированияПроизводная суммы равна сумме производных.Постоянный множитель
- 7. Основные формулы дифференцирования
- 8. Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равныПараллельны ли прямые:
- 9. Пусть дан график функции y=f(x). На нем
- 10. Геометрический смысл производнойЕсли к графику функции
- 11. Геометрический смысл производнойПроизводная в точке
- 12. Вывод уравнения касательнойПусть прямая задана уравнением: уравнение касательной к графику функции
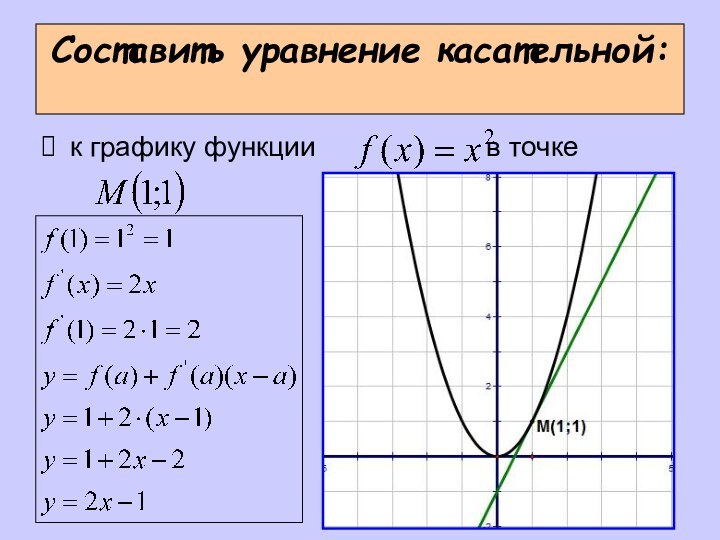
- 13. Составить уравнение касательной:к графику функции
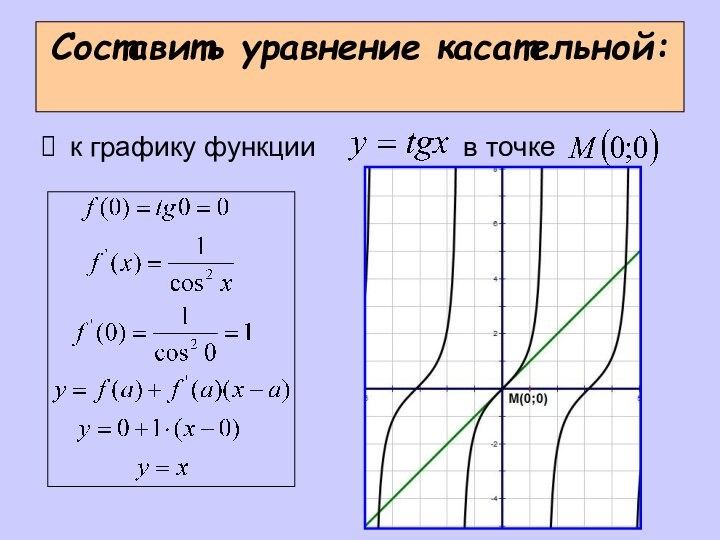
- 14. Составить уравнение касательной:к графику функции в точке
- 15. Алгоритм нахождения уравнения касательной к графику функции
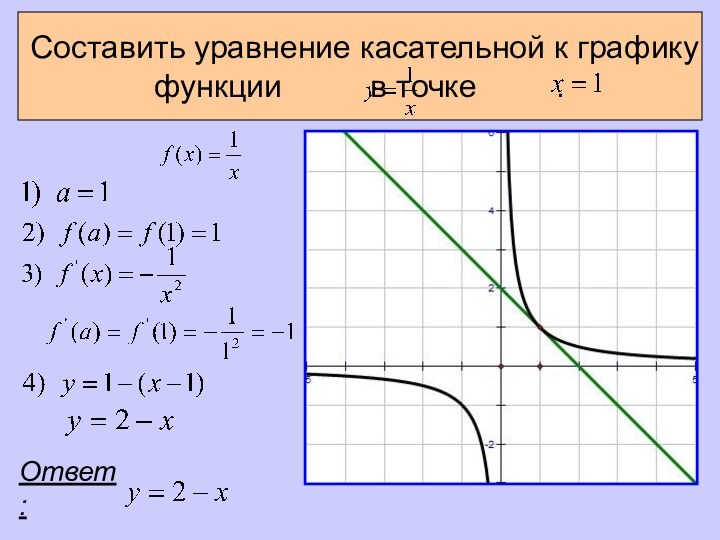
- 16. Составить уравнение касательной к графику функции
- 17. К графику функции
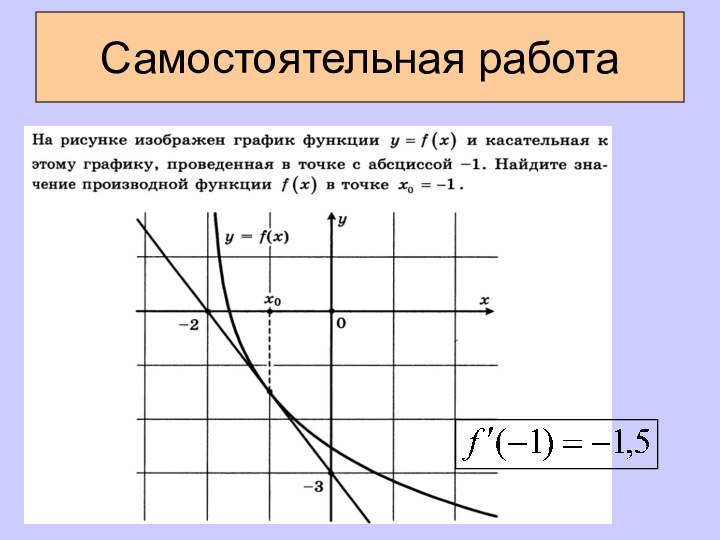
- 19. Самостоятельная работа
- 20. Номера из учебника№ 29.3 (а,в)№ 29.12 (б,г)№ 29.18№ 29.23 (а)
- 21. Ответьте на вопросы:Что называется касательной к графику
- 22. Домашняя работа№ 29.3 (б,г)№ 29.12 (а,в)№ 29.19№ 29.23 (б)
- 23. Скачать презентацию
- 24. Похожие презентации
Верно ли определение?Касательная – это прямая, имеющая с данной кривой одну общую точку.














Слайд 4
На данном уроке:
выясним, что же такое касательная к
графику функции в точке, как составить уравнение касательной;
рассмотрим основные
задачи на составление уравнения касательной.Для этого:
вспомним общий вид уравнения прямой
условия параллельности прямых
определение производной
правила дифференцирования
Формулы дифференцирования
Слайд 5
Определение производной
Пусть функция
определена в некотором интервале, содержащем внутри себя
точку . Дадим аргументу приращение такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции и составимотношение .Если существует предел
отношения при , то указанный предел называют производной функции в точке и обозначают .
Слайд 6
Правила дифференцирования
Производная суммы равна сумме производных.
Постоянный множитель можно
вынести за знак производной.
Производная произведения двух функций равна сумме
двух слагаемых; первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.Производная частного
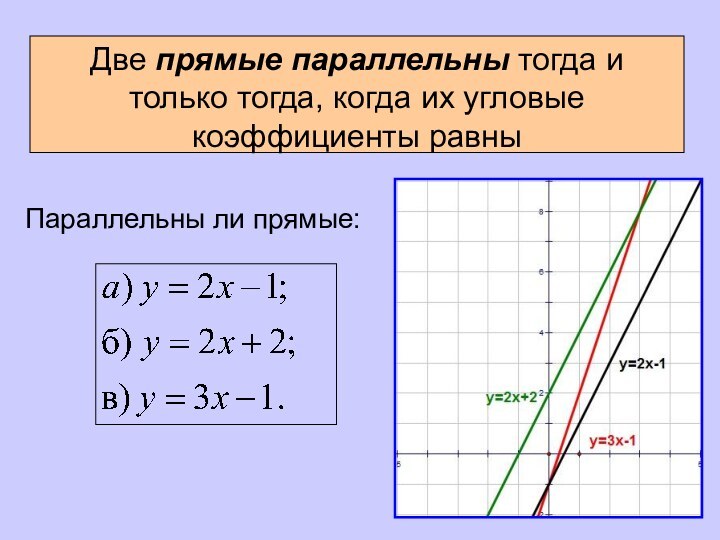
Слайд 8 Две прямые параллельны тогда и только тогда, когда
их угловые коэффициенты равны
Параллельны ли прямые:
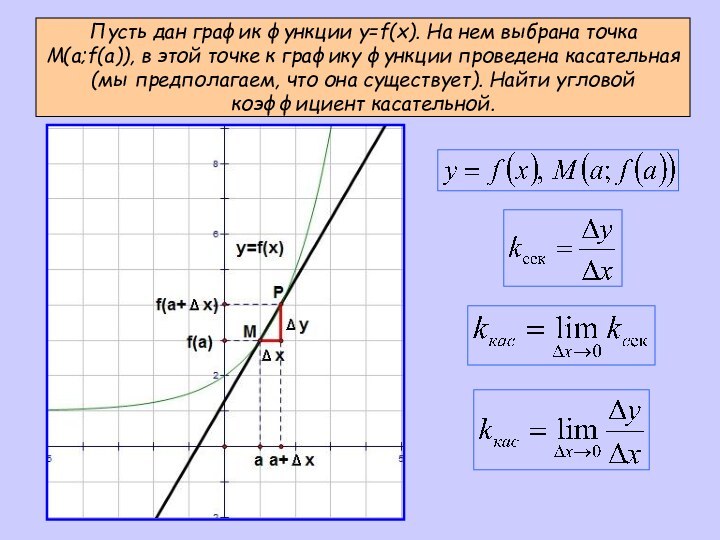
Слайд 9 Пусть дан график функции y=f(x). На нем выбрана
точка M(a;f(a)), в этой точке к графику функции проведена
касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.
Слайд 10
Геометрический смысл производной
Если к графику функции y
= f (x) в точке
можно провести касательную, непараллельную оси у, то выражает угловой коэффициент касательной
Слайд 11
Геометрический смысл производной
Производная в точке
равна
угловому коэффициенту
касательной к
графику функции
y = f(x) в этой точке.
Т.е.
Причем, если :
.
Слайд 12
Вывод уравнения касательной
Пусть прямая задана уравнением:
уравнение касательной
к
графику функции
Слайд 15
Алгоритм нахождения уравнения касательной к графику функции y=f(x).
Обозначим
абсциссу точки касания буквой x=a.
Вычислим
.Найдем и .
Подставим найденные числа a , в формулу