- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии для внеклассной работы Как Пахом землю делил
Содержание
- 2. Геометрическая экономия,
- 3. Этот доклад, смысл названия которого станет понятно
- 4. -А цена какая будет?
- 5. -А цена какая будет? – говорит Пахом.
- 6. -А цена какая будет? – говорит Пахом.- Цена у нас одна: 1000 рублей за день.
- 7. -А цена какая будет? – говорит Пахом.-
- 8. -А цена какая будет? – говорит Пахом.-
- 9. -А цена какая будет? – говорит Пахом.-
- 10. Нас в этом рассказе интересует его математическая часть.
- 11. Нас в этом рассказе интересует его математическая часть.Вопрос №1:
- 12. Нас в этом рассказе интересует его математическая
- 13. Внимательно прочитав рассказ, извлекая из него все данные мы сможем составит условия геометрической задачи. Читаем:
- 14. Прежде всего в рассказе сказано, что Пахом
- 15. Прежде всего в рассказе сказано, что Пахом
- 16. Значит первая сторона четырёхугольника имела в длину около 10 верст. I сторона – 5+5=10 верст
- 17. О второй стороне численных данных в рассказе нет. II сторона – ? верст
- 18. Длина третьей стороны в рассказе указана прямо
- 19. Также прямо дана длина и четвёртой стороны:
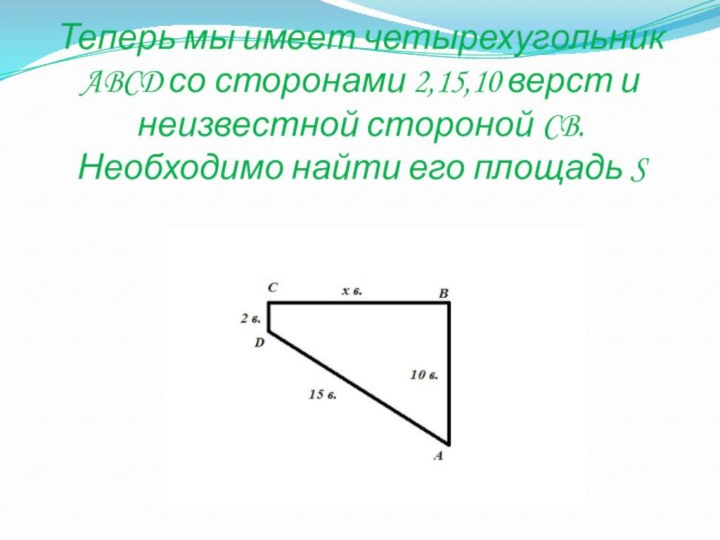
- 20. Теперь мы имеет четырехугольник ABCD со сторонами
- 21. Теперь мы имеет четырехугольник ABCD со сторонами
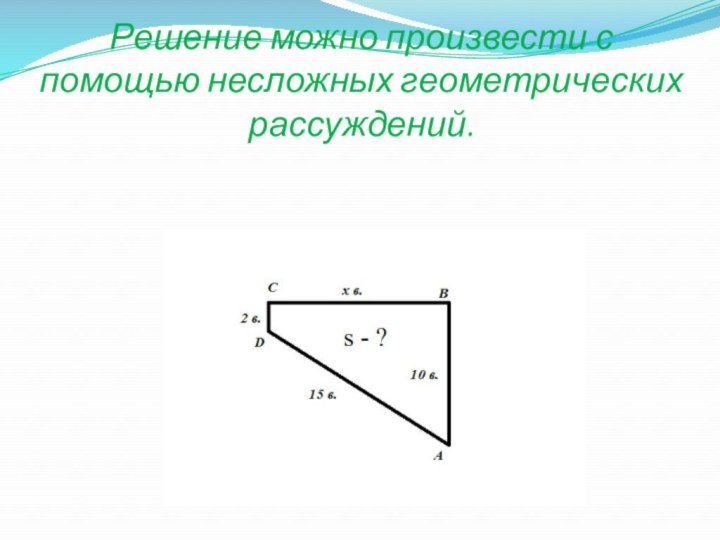
- 22. Решение можно произвести с помощью несложных геометрических рассуждений.
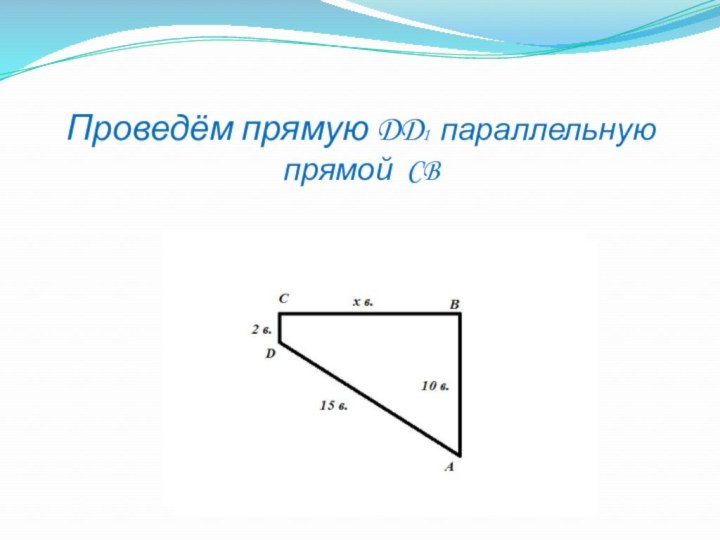
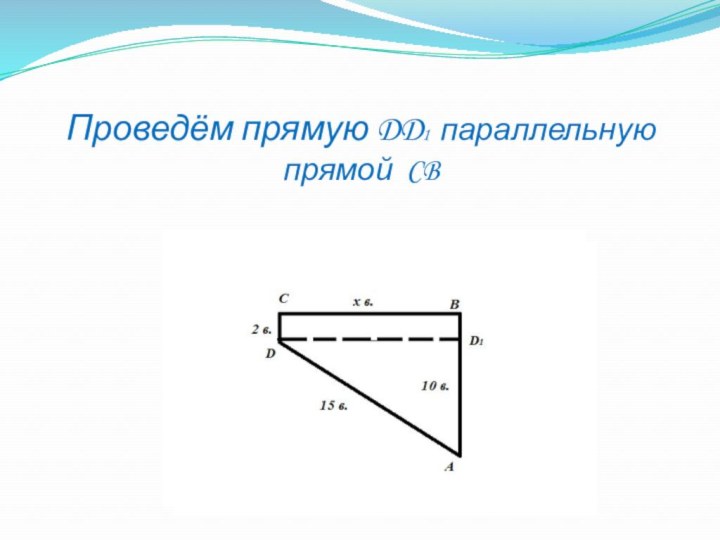
- 23. Проведём прямую DD1 параллельную прямой CB
- 24. Проведём прямую DD1 параллельную прямой CB
- 25. Теперь мы имеем прямоугольный треугольник ADD и
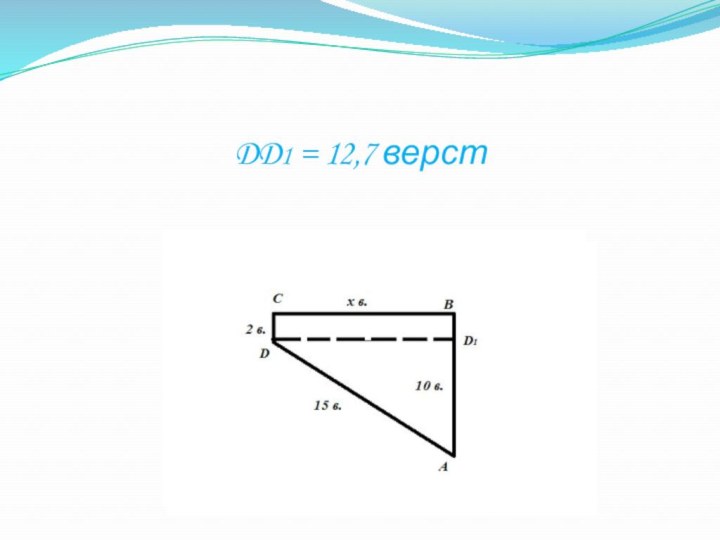
- 26. DD1 = 12,7 верст
- 27. DD1 = 12,7 верст
- 28. Так как CBD1D- прямоугольник, то CB=DD1 = 12,7 верстам
- 29. Вычисляем площадь прямоугольной трапеции ABCD.
- 30. Площадь трапеции ABCD равна 78 квадратным верстам
- 31. 78 квадратные версты примерно равны 94 квадратным километрам
- 32. Получается, что идя по сторонам трапеции, Пахом
- 33. Получается, что идя по сторонам трапеции, Пахом
- 34. Получается, что идя по сторонам трапеции, Пахом
- 35. Его первоначальным намерением было бежать по сторонам
- 36. Прямоугольников с периметром 40 вёрст может быть
- 37. Прямоугольников с периметром 40 вёрст может быть
- 38. Прямоугольников с периметром 40 вёрст может быть
- 39. Прямоугольников с периметром 40 вёрст может быть
- 40. Прямоугольников с периметром 40 вёрст может быть
- 41. Мы видим, что у всех приведённых прямоугольников,
- 42. Мы видим, что у всех приведённых прямоугольников,
- 43. Мы видим, что у всех приведённых прямоугольников,
- 44. Мы видим, что у всех приведённых прямоугольников,
- 45. Мы видим, что у всех приведённых прямоугольников,
- 46. Следовательно, на вопрос нельзя дать однозначный ответ.
- 47. Следовательно, на вопрос нельзя дать однозначный ответ.
- 48. Сравнивая наши прямоугольники мы замечаем, что чем
- 49. Если бы Пахом бежал по сторонам квадрата,
- 54. Замечательное свойство квадрата
- 55. Замечательное свойство квадрата
- 56. Замечательное свойство квадрата
- 57. Замечательное свойство квадрата: он всегда имеет большую площадь, чем любой прямоугольник, равного с ним периметра.
- 58. Замечательное свойство квадрата: он всегда имеет большую площадь, чем любой прямоугольник, равного с ним периметра.
- 59. Доказательство:
- 60. Скачать презентацию
- 61. Похожие презентации
Геометрическая экономия, илинахождение формы геометрической плоской фигуры заданного периметра, при котором она имеет наибольшую площадь.
Слайд 2 Геометрическая экономия,
или
фигуры заданного периметра, при котором она имеет наибольшую площадь.Слайд 3 Этот доклад, смысл названия которого станет понятно вам
в дальнейшем, я хочу начать отрывком из рассказа Л.Н.Толстого
«Много ли человеку земли нужно».
Слайд 7
-А цена какая будет? – говорит Пахом.
- Цена
у нас одна: 1000 рублей за день.
Не понял
Пахом.
Слайд 8
-А цена какая будет? – говорит Пахом.
- Цена
у нас одна: 1000 рублей за день.
Не понял
Пахом.- Какая это мера – день? Сколько в ней десятин будет?
Слайд 9
-А цена какая будет? – говорит Пахом.
- Цена
у нас одна: 1000 рублей за день.
Не понял
Пахом.- Какая это мера – день? Сколько в ней десятин будет?
- Мы этого – говорят – не умеем считать. А мы за день продаём: сколько в день обойдешь, то и твое. И платишь ты за это 1000 рублей.
Слайд 12
Нас в этом рассказе интересует его математическая часть.
Вопрос
№1:
Можно ли по данным, представленных в рассказе определить
сколько квадратных вёрст обежал Пахом за день?Слайд 13 Внимательно прочитав рассказ, извлекая из него все данные
мы сможем составит условия геометрической задачи.
Читаем:
Слайд 14 Прежде всего в рассказе сказано, что Пахом бежал
по сторонам четырехугольника: «…Одна упряжка прошла, - думает Пахом.
– А их четыре во дню, надо поворачивать…»Слайд 15 Прежде всего в рассказе сказано, что Пахом бежал
по сторонам четырехугольника: «…Одна упряжка прошла, - думает Пахом.
– А их четыре во дню, надо поворачивать…»О первой стороне мы читаем: «… Верст пять прошёл. Пройду ещё вёрст с пяток, тогда и влево буду загибать…»
Слайд 16 Значит первая сторона четырёхугольника имела в длину около
10 верст.
I сторона – 5+5=10 верст
Слайд 18 Длина третьей стороны в рассказе указана прямо –
«…По третьей стороне всего версты 2 прошёл». III сторона –
2 верстыСлайд 19 Также прямо дана длина и четвёртой стороны: «До
места всё те же верст пятнадцать» IV сторона – 15
верст.Слайд 20 Теперь мы имеет четырехугольник ABCD со сторонами 2,15,10
верст и неизвестной стороной CB. Необходимо найти его площадь
SСлайд 21 Теперь мы имеет четырехугольник ABCD со сторонами 2,15,10
верст и неизвестной стороной CB. Необходимо найти его площадь
SСлайд 25 Теперь мы имеем прямоугольный треугольник ADD и прямоугольник
CBD1D . Из теоремы Пифагора находим третью сторону по
двум другим.Слайд 32 Получается, что идя по сторонам трапеции, Пахом обежал
78 кв. верст. При этом он пробежал 13+10+2+15=40 верст
(48 км).Слайд 33 Получается, что идя по сторонам трапеции, Пахом обежал
78 кв. верст. При этом он пробежал 13+10+2+15=40 верст
(48 км). Вопрос №2.Слайд 34 Получается, что идя по сторонам трапеции, Пахом обежал
78 кв. верст. При этом он пробежал 13+10+2+15=40 верст
(48 км). Вопрос №2. Мог ли Пахом обежать большую площадь пройдя те же 40 верст?Слайд 35 Его первоначальным намерением было бежать по сторонам прямоугольника,
а трапеция получилась в результате плохого расчёта. Интересно узнать,
выгадал он, или прогадал?Слайд 36 Прямоугольников с периметром 40 вёрст может быть много,
и каждый из них имеет различную площадь. Вот ряд
примеров:Слайд 37 Прямоугольников с периметром 40 вёрст может быть много,
и каждый из них имеет различную площадь. Вот ряд
примеров: 14х6=84Слайд 38 Прямоугольников с периметром 40 вёрст может быть много,
и каждый из них имеет различную площадь. Вот ряд
примеров: 14х6=84 13х7=91Слайд 39 Прямоугольников с периметром 40 вёрст может быть много,
и каждый из них имеет различную площадь. Вот ряд
примеров: 14х6=84 13х7=91 12х8=96Слайд 40 Прямоугольников с периметром 40 вёрст может быть много,
и каждый из них имеет различную площадь. Вот ряд
примеров: 14х6=84 13х7=91 12х8=96 11х9=99Слайд 41 Мы видим, что у всех приведённых прямоугольников, площадь
больше нашей трапеции. Но есть и такие прямоугольники, меньшие
чем она.Слайд 42 Мы видим, что у всех приведённых прямоугольников, площадь
больше нашей трапеции. Но есть и такие прямоугольники, меньшие
чем она. 18х2=36Слайд 43 Мы видим, что у всех приведённых прямоугольников, площадь
больше нашей трапеции. Но есть и такие прямоугольники, меньшие
чем она. 18х2=36 19х1=19Слайд 44 Мы видим, что у всех приведённых прямоугольников, площадь
больше нашей трапеции. Но есть и такие прямоугольники, меньшие
чем она. 18х2=36 19х1=19 19,5х0,5=9,25Слайд 45 Мы видим, что у всех приведённых прямоугольников, площадь
больше нашей трапеции. Но есть и такие прямоугольники, меньшие
чем она. 18х2=36 19х1=19 19,5х0,5=9,25 17х3=51Слайд 46 Следовательно, на вопрос нельзя дать однозначный ответ. Есть
прямоугольники и с большей площадью, чем наша трапеция, и
с меньшей, при одинаковом периметре. Но можно дать ответ на другой вопрос:Слайд 47 Следовательно, на вопрос нельзя дать однозначный ответ. Есть
прямоугольники и с большей площадью, чем наша трапеция, и
с меньшей, при одинаковом периметре. Но можно дать ответ на другой вопрос: какая из прямоугольных фигур с заданным периметром имеет наибольшую площадь?Слайд 48 Сравнивая наши прямоугольники мы замечаем, что чем меньше
разность сторон прямоугольника, тем больше его площадь. Следовательно когда
разности не будет вообще, то есть, когда фигура станет квадратом, тогда площадь фигуры станет равна 10х10=100 кв. верст. Легко видно, что квадрат превосходит любой прямоугольник одинакового с ним периметра.Слайд 49 Если бы Пахом бежал по сторонам квадрата, а
не трапеции, то пробежав 40 верст он бы обежал
100 кв. верст, то есть на 22 кв. версты больше.
Слайд 57
Замечательное свойство квадрата:
он всегда имеет большую площадь,
чем любой прямоугольник, равного с ним периметра.
Слайд 58
Замечательное свойство квадрата:
он всегда имеет большую площадь,
