Слайд 2
Трансляциялық симметрия
Трансляциялық симметрия – қарастырып отырған жүйені трансляция
векторы деп аталатын векторға жылжытқанда қасиеттері өзгермейтін симметрия.
Трансляциялық
симметрия кристаллдарға да тән. Трансляция векторларының саны шексіз көп болғанымен, олар өзара тәуелді. Кристалл тордың барлық трансляциялық векторларының ішінен 3 сызықты тәуелсіз векторлар таңдап аламыз, бірақ осы векторлардың әрқайсысы қалған екеуінің бүтін- сызықтық комбинациясы болуы тиіс. Осы үш вектор кристаллдық тордың базисін құрайды.
Зерттеулер трансляциялық симметрия бұрылу бұрышы θ=2π/n болғанда ғана орындалатынын көрсетеді. Мұндағы n =1,2,3,4,5,6 мәндерін қабылдайды.
180,120,90,60 градусқа бұрылған кезде кристаллдағы атомдардың орналасуында ешқандай өзгеріс болмайды.
Слайд 3
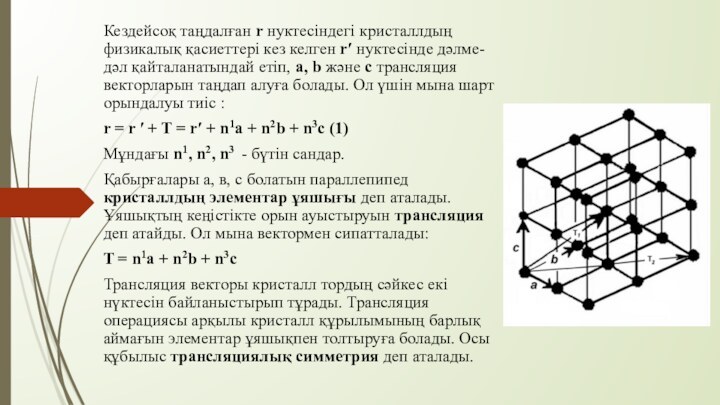
Кездейсоқ таңдалған r нуктесіндегі кристаллдың физикалық қасиеттері кез
келген r′ нуктесінде дәлме-дәл қайталанатындай етіп, a, b және
c трансляция векторларын таңдап алуға болады. Ол үшін мына шарт орындалуы тиіс :
r = r ′ + T = r′ + n1a + n2b + n3c (1)
Мұндағы n1, n2, n3 - бүтін сандар.
Қабырғалары а, в, с болатын параллепипед кристаллдың элементар ұяшығы деп аталады. Ұяшықтың кеңістікте орын ауыстыруын трансляция деп атайды. Ол мына вектормен сипатталады:
T = n1a + n2b + n3c
Трансляция векторы кристалл тордың сәйкес екі нүктесін байланыстырып тұрады. Трансляция операциясы арқылы кристалл құрылымының барлық аймағын элементар ұяшықпен толтыруға болады. Осы құбылыс трансляциялық симметрия деп аталады.
Слайд 4
1848 жылы О.Бравэ элементар ұяшықтарды төрт тип бойынша
: P, I, A(B,C), F және жеті кристаллдық жүйеге
,яғни сингонияға ( әртүрлі жеті координат жүйесі) жіктеуді ұсынды. Классификация келесі қасиеттерге сүйене отырып жасалды:
Симметрия центрі ( ұяшықтың симметрия центрі бар, егер екі нүктені немесе жазықтықты қосатын түзудің дәл центрінен бір нүкте таңдап ала алсақ)
Симметрия жазықтығы ( ұяшықтың симметрия жазықтығы бар, егер ұяшықты қаққа бөлгенде, оның бөліктері сол жазықтықта айналық бейнеленсе)
Симметрия осьі ( егер ұяшық 360 градусқа айналдырғанда өзі тұрған орынға эквивалентті жерге бірнеше рет орын ауыстырса , ұяшықтың симметрия осьі бар)
Бравэ ұяшықтары жиі кездесетін 14 кристалл құрылымын сипаттайды.
1867 жылы А.В.Гадолина мүмкін болатын 32 ұяшық ұсынған ( бұрылулар мен шағылуларды ескерген)
1890 жылы Е.С.Федоров мүмкін болатын ұяшықтардың толық тізімін берді. Тізім бойынша ұяшықтар саны 230-ға жетті.
Слайд 5
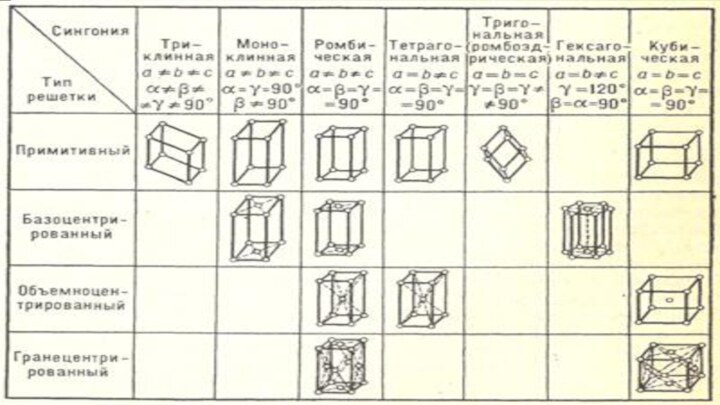
Кез келген кристаллды төмендегідей типтерге жіктеуге болады:
Р –
примитивті ұяшық, бір түйінді элементар ұяшық
A,B,C – бір қырға
екі түйін сәйкес келетін тор: А- түйін а қабырғада орналасқан, В- в қабырғада орналасқан, С- базоцентрленген тор
І – объемноцентрированная решетка
Ғ – гранецентрированная решетка, А+В+С, төрт түйінді элементар ұяшық
Слайд 6
Әрбір кристаллды келесі жеті кристаллографиялық жүйелердің- сингониялардың біріне

жатқызуға болады:
Триклинді (а) кристаллдар: кристалл қабырғалары a, b және
c өзара α≠β≠γ≠90˚ бұрыштар жасайды (K2Cr2O7, CuSO4·5H2O).
Моноклинді (b) кристаллдар: екі қабырға (а мен с)арасындағы бұрыш β,ал үшінші қабырға а мен с-ға тік бұрыш жасап орналасқан, α= γ=90˚; β≠90˚. (моноклинді күкірт, KClO3)
Ромбтық (c) кристаллдар: қабырғалары өзара тең емес a, b, c, бірақ өзара перпендикуляр - α=β=γ=90˚ (I2, күкірт).
Тригональды (d)(ромбоэдрлік) кристаллдар – элементар ұяшық ,a,α (a=b=c,α=β=γ90о) (кальцит,As).
Тетрагональды (e) кристаллдардың екі қабырғасы өзара тең а(a=b), ал үшіншісі с-ға тең, барлық қабырғалар өзара перпендикуляр α=β=γ=90˚ (SnO2, белое олово).
Гексагональды (f) кристаллдардың екі қабырғасы өзара тең а(a=b), ал үшіншісі с-ға тең, (a=b, α=β=90˚, γ=120˚) (кварц,мұз, Mg, Zn-гексагон.)
Кубтық (g) кристаллдар өзара тең әрі перпендикуляр қабырғалармен сипатталады: а(a=b=c); α=β=γ=90˚ (NaCl,Fe,Cu,алмаз).