Презентация на тему Линейная функция 11 класс

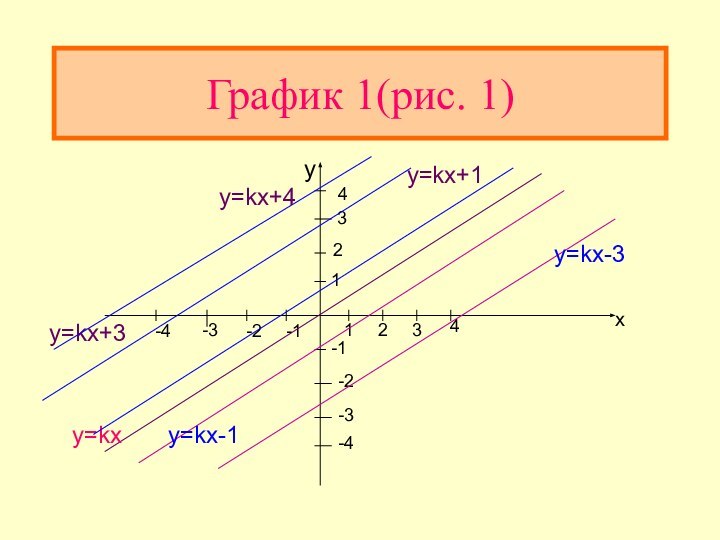
1 (рис. 1)
Пример 1
Пример 2
Замечание к примерам
Пример 3
Замечание к

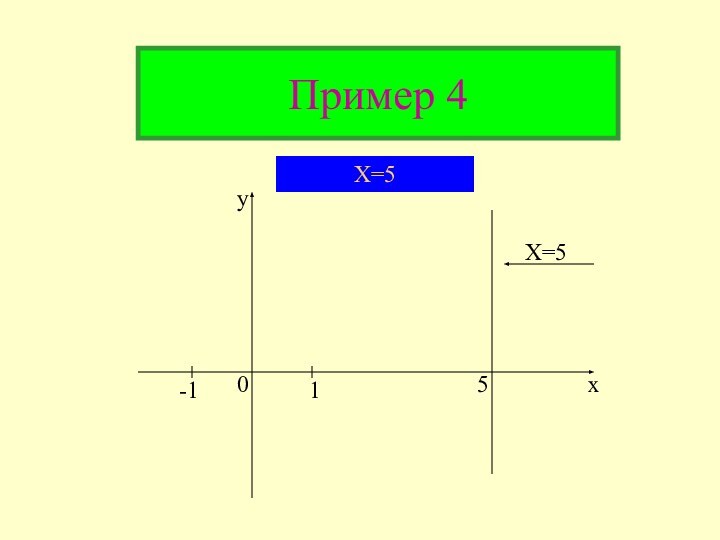
примеру 3
Пример 4
Пример 5
Частный случай
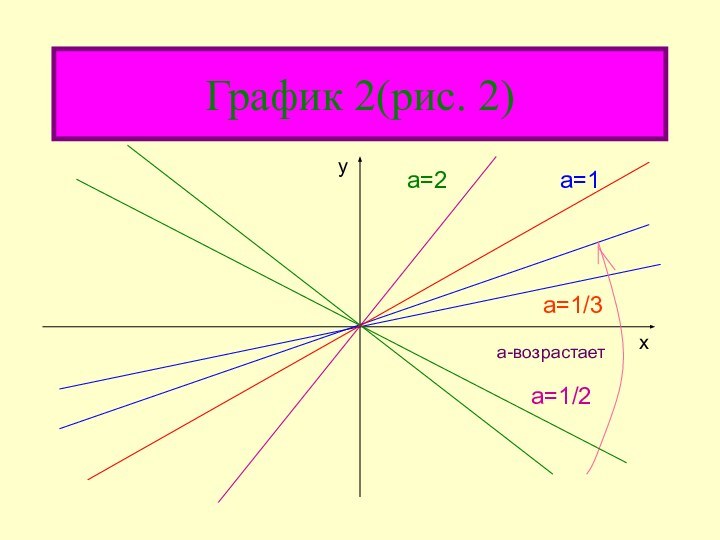
График 2 (рис. 2)
Пример 6

Содержание

не линейную: y(x)=kx+b, где k и b- некоторые константы,

x и y- переменные.
График линейной функции- прямая линия. Прямая Y=kx+l пересекает ось ординат в точке (o;l) и ось абсцисс в точке (-l/k;o).
Число k- угловой коэффициент прямой.

степени, т. е. функция вида y=kx+b.Линейная функция определена на

всей числовой потому, что ее график есть прямая линия.
Рассмотрим два значения аргумента x1 и x2, им соответствует значения линейной функции y1=ax1+b и y2=ax2+b. Изменение аргумента на величине x2-x1 называется изменение функции на величине y2-y1=a(x2-x1) при этом отношении изменения функции к изменению аргумента равно а: (y2-y1)/(x2-x1)=a

изменение функции пропорционально изменению аргумента, и это есть характеристическое

свойство линейной функции. Поэтому с помощью линейной функции описывается пропорциональные зависимости.

различными шкалами температур абсолютная температура tk (по Кельвину) связана

с температурой tc на шкале Цельсия формулой tc=tk+273°, а переход от температуры по Фаренгейту (шкале, принятой до сих пор в Англии и США) tф к температуре на шкале Цельсия tс выражается такой линейной функцией: tф=1,8tс+32° (на шкале Цельсия промежуток между точкой замерзания и точкой кипения разделен на 100 частей, а на шкале Фаренгейта на 180, и 0°С соответствует 32°Ф)

не равно 0) получается из графика функции y=ax параллельным

переносом на b единиц вверх при b>0 и на b единиц вниз при b<0 (рис. 2). Поскольку прямая определяется своими двумя точками, то для построения графика достаточно лишь двух ее точек.
Линейная функция простейшая и, можно сказать, важнейшая среди всех функций. Многие физические законы выражаются с помощью линейной функции (мы уже говорили о пройденном пути при постоянной скорости), но важно то, что целый ряд сложных нелинейных зависимостей «в малом» можно считать линейным.

Имеем линейную функцию:

, где k=2/3; l=2. Так как k=2/3>0, то функция возрастает на всей области определения.

Пример 1

x

-3

2

-1

1

0

y

2/3x4y=1

Y=1/10x+1/4; где k=-1/10; l=1/4
Так как k=-1/10<0, то функция Y=-1/10x+1/4 убывает на всей области определения.

y

x

1 2

1

1

Y=-1/10x+1/4

является частным случаем функции y=kx+b (при l=0).
Замечание 2 к

примеру 2

Графиком линейной функции y=l(k=0) является прямая, параллельная оси абсцисс, пересекающая ось ординат в точке(o;l)

Поскольку нарушается условие однозначности при определении функции- каждому значению

x должно соответствовать единственное значение y.

x

y

0

-1

-2

Y=-2

1

параллельная оси пересекающая ось Oy, абсцисс в точке (k;o)

длине l, а именно p=kl (здесь k-цена одного метра

ткани); при равномерном движении с постоянной скоростью v пройденный путь s пропорционален времени t и выражается формулой s=vt, т. е. s-линейная функция t.

пропорциональная зависимость y=kx, т.е.линейная функция при b=0. график этой

функции есть прямая, проходящая через начало координат (рис.1). Число а называется угловым коэффициентом прямой и равен tg угла альфа, образованного прямой с положительным направлением оси 0x.