четырехугольной пирамиды равна α. Определить величину двугранного угла между
боковой гранью и основанием пирамиды. Для каких α задача имеет решение?Ответ:
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











Ответ:
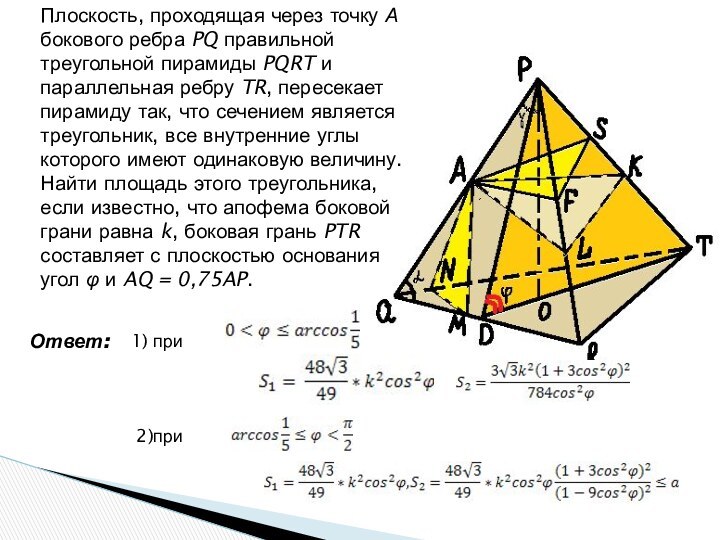
Ответ:
2)при
1) при
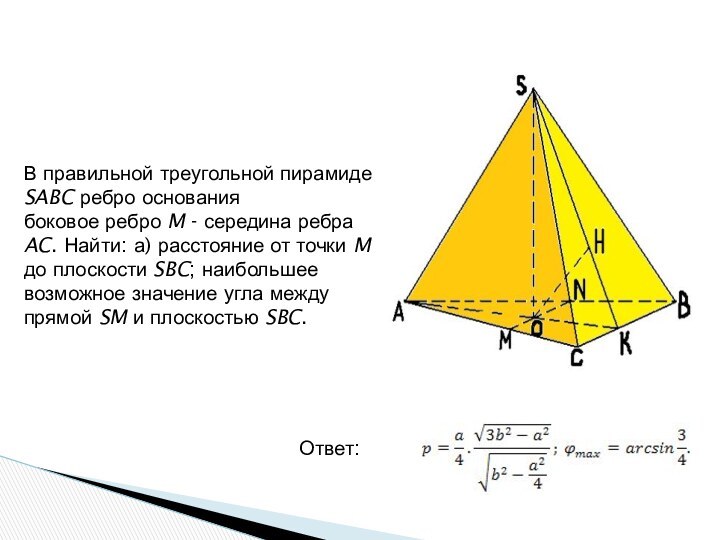
Ответ:
Ответ:
Ответ:
Ответ:
Ответ:
Ответ:
Ответ:
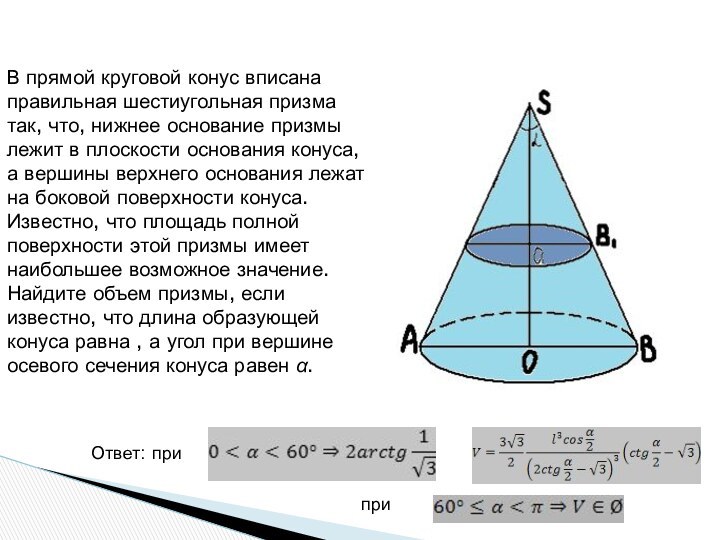
Ответ: при
при
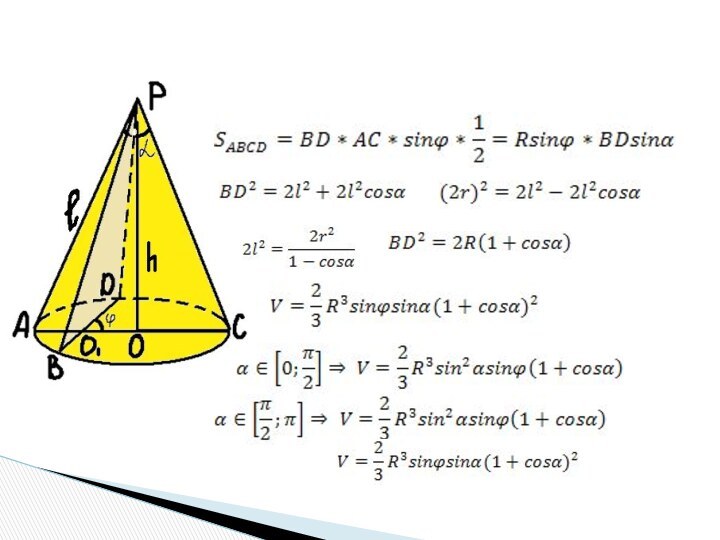
r – радиус основания, тогда
,
б)
т.е. в этом случае