- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Случайные величины и их законы распределения
Содержание
- 2. Случайные величины и их законы распределения
- 3. Определение случайной величиныэто числовая функция, заданная на множестве элементарных событий с областью значений вИли в
- 4. теперь под случайным событием понимается попадание случайной величины в некоторое конечное или бесконечное числовое множествоСЛУЧАЙНОЕ СОБЫТИЕ
- 5. Обычно рассматривают два вида случайных величин: дискретные и непрерывные.
- 6. Дискретная случайная величинапринимает конечное или счетное множество
- 7. Непрерывные случайные величины принимают любое значение в некотором
- 8. Закон распределения дискретной случайной величины Для полного
- 9. Ряд распределения
- 10. Функция распределения случайной величины
- 11. Свойства функции распределения
- 12. Свойства функции распределения
- 13. Свойства функции распределенияДля дискретной СВ
- 14. Свойства функции распределения
- 15. Непрерывная случайная величинаСлучайная величина X называется непрерывной, если ее функцияраспределения непрерывна
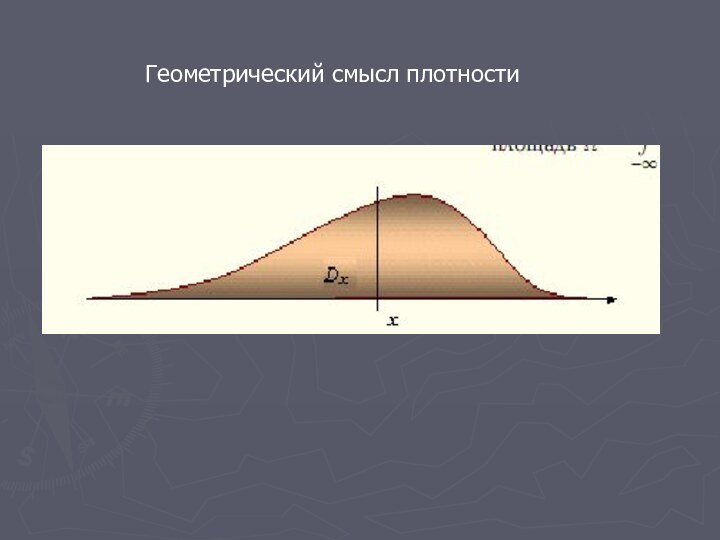
- 17. Геометрический смысл плотности
- 18. ПримерыВырожденное распределение(Распределение константы)Распределение Бернулли (Распределение индикатора события)
- 19. Скачать презентацию
- 20. Похожие презентации
Случайные величины и их законы распределения


















Слайд 3
Определение случайной величины
это числовая функция, заданная на множестве
элементарных событий
Слайд 4 теперь под случайным событием понимается попадание случайной величины
в некоторое конечное или бесконечное числовое множество
СЛУЧАЙНОЕ СОБЫТИЕ
Слайд 6
Дискретная случайная величина
принимает конечное или счетное множество значений
она
используется при описании измерений, принимающих целочисленные значения:
Число дефектных изделий
в партии, число телефонных вызовов за смену,
число неисправностей в приборе и т.д. и может быть записана в виде последовательности





























