Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Ключевые задачи в процессе обучения школьников решению задач по геометрии

Содержание

« Каждая решенная мною задача становилась образцом, который служил впоследствии для решения других задач »
Ключевые задачи в процессе обучения школьников решению задач по геометрии « Каждая решенная мною задача становилась образцом, который служил впоследствии для решения Основная цель школьного курса геометрии – обучение решению геометрических задачВ практической деятельности Понимание учащимися природы и структуры математических задач.Ликвидацию перегрузки учащихся.Гарантию успеха в решении учить методам решения математических задач облегчает поиск решения дает возможность индивидуализировать процесс Математическая задача называется ключевой, если ее содержание либо метод ее решения используется Ключевая задачаКлючевая задача – это отдельная методическая единицаЗадача - фактЗадача-методЗадача-факт и метод 1)проанализировать, какие умения должны быть сформированы у учащихся в результате изучения данной 1 Аналитический : анализ любой задачи позволяет вычленить из нее подзадачи2) Основан начинать лучше с самых простых ключевых задач; задачи, выходящие за рамки школьной желательно чередовать задачи с обширными записями и те, которые не предполагают громоздких умение школьников распознавать ключевые задачи;умение решать ключевые задачи;умение правильно оформлять решение Специальные уроки Ознакомление учащихся с решением указанных задач Систематизации методов решения задач Ключевые задачи 1. Медианы в треугольнике пересекаются в одной точке и делятся в ней 1 Сумма квадратов медиан треугольника равна суммы квадратов его сторон.2. Сумма квадратов Ключевая задача. Докажите, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна 1. Центр описанной около прямоугольного треугольника окружности лежит на АСBMADCB 1. Найдите отношение суммы квадратов длин всех медиан треугольника к сумме квадратов Задачи системы. Задачи на применение ключевой задачи Ключевая задача «Свойства биссектрисы угла треугольника» Расстояние от вершины прямого угла до гипотенузы равно а, а до точки 1. В треугольнике АВС С= 90°, СD – биссектриса, AD=m, BD=n Найдите 4. В прямоугольный треугольник с углом 60° вписан ромб со стороной, 1. Концы лестницы скользят по стенкам угла. Какую траекторию описывает при этом Свойства треугольника, образованного основаниями высот данного остроугольного треугольника. Задачи системы. Ключевая задача. Середины сторон произвольного четырехугольника являются вершинами параллелограмма.  Следствия. 1. Докажите, что медианы треугольника пересекаются в одной точке и она делит Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Ключевые задачи по теме «параллелограмм» Ключевые задачи по теме «параллелограмм»Биссектрисы смежных углов параллелограмма пересекаются под прямым углом. Ключевые задачи по теме «параллелограмм»Биссектрисы противоположных углов параллелограмма параллельны Ключевые задачи по теме «параллелограмм»Высоты параллелограмма, опущенные из одной вершины, образуют угол, Ключевые задачи по теме «параллелограмм»Любой отрезок с концами на сторонах параллелограмма, проходящий 1) AOD подобен СOВ, k=a/b(коэффициент подобия равен отношению оснований трапеции) 2)S1 = Рис. 2. В равнобокой трапеции Рис. 2 а. – углы при основании Если в равнобокую трапецию вписана окружность, то ее боковая сторона равна средней 1) Если трапеция равнобокая, то около нее можно описать окружность. 2) Если Если окружность вписана в трапецию, то 1) суммы противоположных сторон трапеции равны «Обучение математике имеет смысл только тогда, когда оно учит думать, решать задачи. Спасибо за внимание!
Слайды презентации

Слайд 2 « Каждая решенная мною задача становилась образцом, который

« Каждая решенная мною задача становилась образцом, который служил впоследствии для

служил впоследствии для решения других задач »



Рене Декарт
(31 марта 1596 –
11февраля 1650)




Слайд 3 Основная цель школьного курса геометрии – обучение решению

Основная цель школьного курса геометрии – обучение решению геометрических задачВ практической

геометрических задач

В практической деятельности закрепляются теоретические знания

Развивается подлинная

творческая активность

Развивается мышление

Слайд 4 Понимание учащимися природы и структуры математических задач.

Ликвидацию перегрузки

Понимание учащимися природы и структуры математических задач.Ликвидацию перегрузки учащихся.Гарантию успеха в

учащихся.

Гарантию успеха в решении всех школьных задач, предлагаемых на

тестировании, ОГЭ и ЕГЭ.

Рациональное использование учебного времени.

Воспитание у учащихся веры в свои способности.

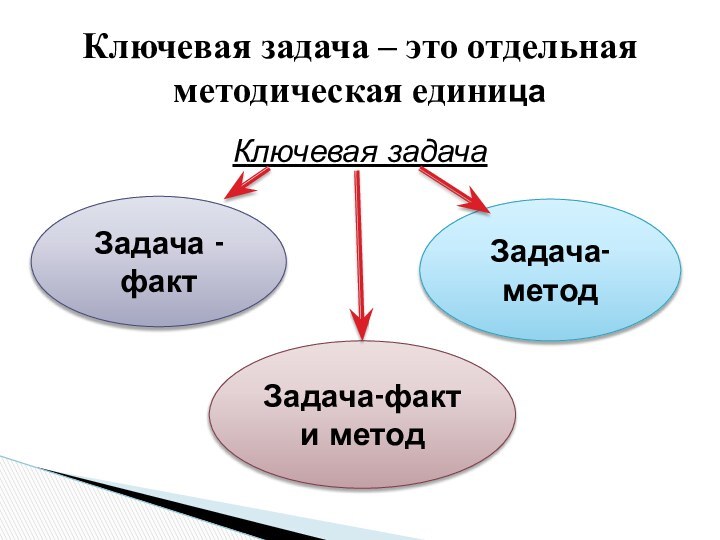
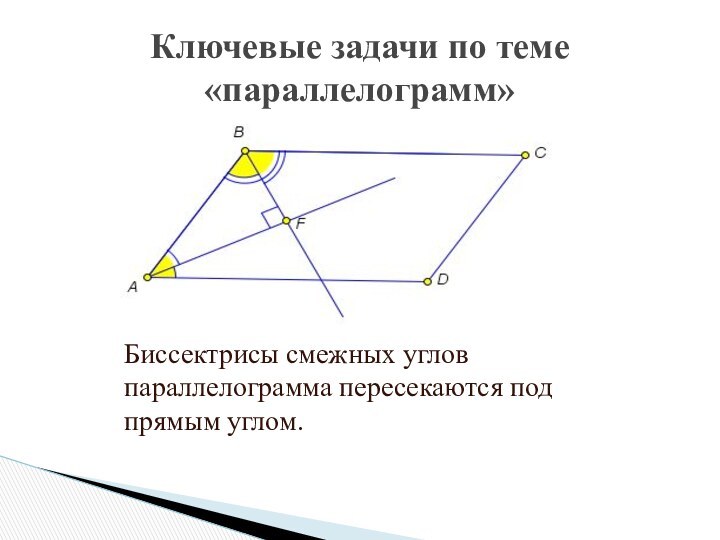
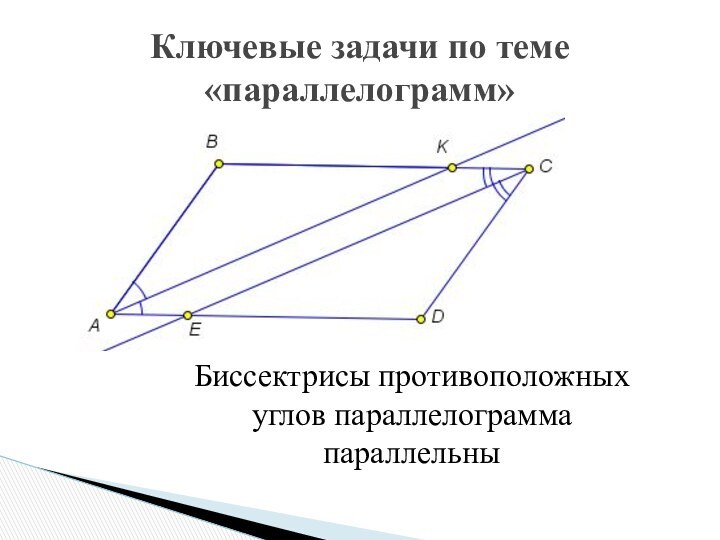
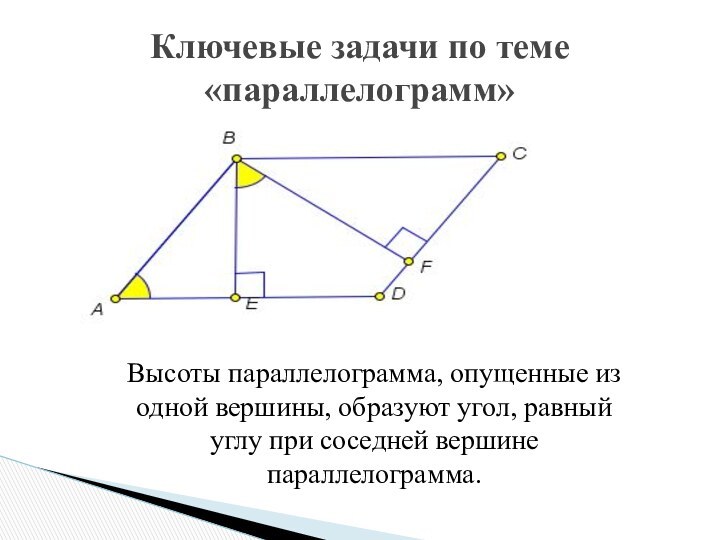
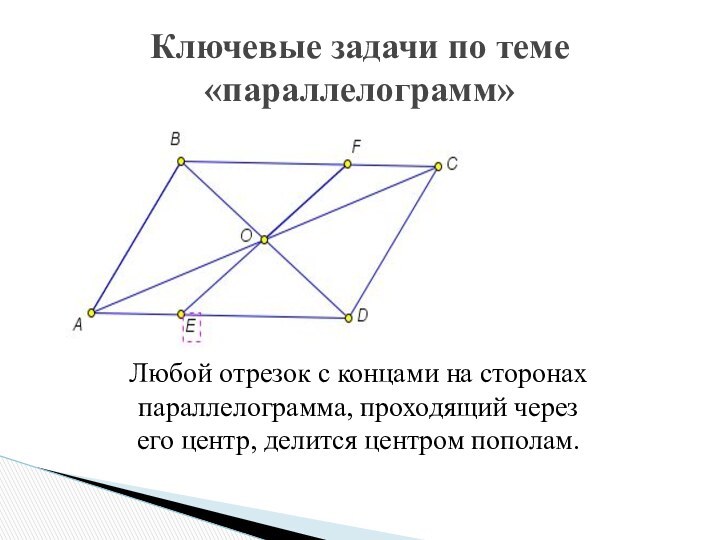
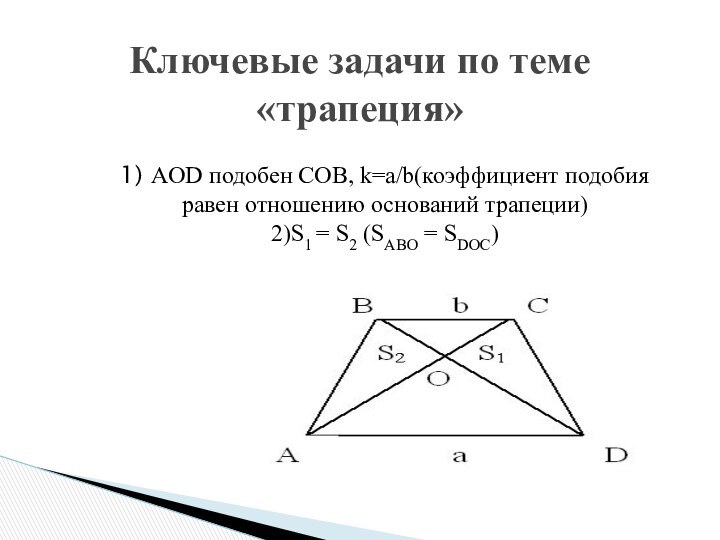
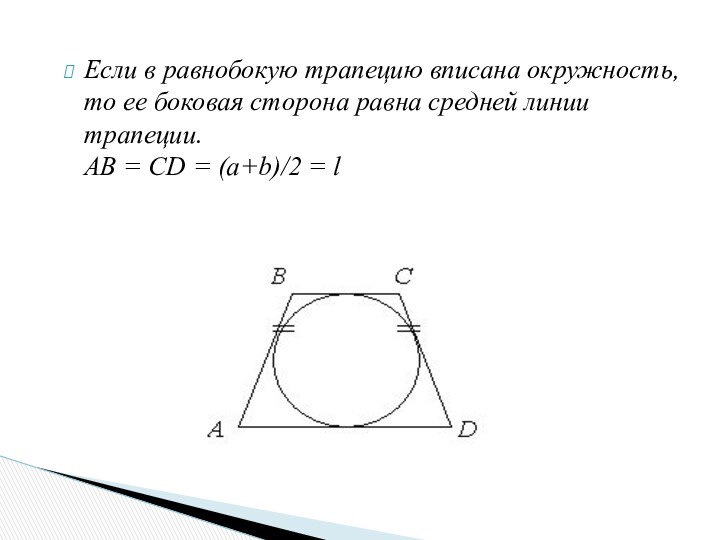
Метод ключевых задач обеспечивает

Слайд 5
учить методам решения математических задач

облегчает поиск решения

учить методам решения математических задач облегчает поиск решения дает возможность индивидуализировать



дает возможность индивидуализировать процесс их решения
Применение ключевых задач

позволяет

Слайд 6 Математическая задача называется ключевой, если ее содержание либо

Математическая задача называется ключевой, если ее содержание либо метод ее решения

метод ее решения используется при решении других задач .

Слайд 7 Ключевая задача
Ключевая задача – это отдельная методическая единица
Задача

Ключевая задачаКлючевая задача – это отдельная методическая единицаЗадача - фактЗадача-методЗадача-факт и метод

- факт
Задача-метод
Задача-факт и метод

Слайд 8
1)проанализировать, какие умения должны быть сформированы у учащихся

1)проанализировать, какие умения должны быть сформированы у учащихся в результате изучения

в результате изучения данной темы;

2)соотнести просматриваемые задачи по

теме с планируемыми умениями;

3) выделить то минимальное их число, овладев решениями которых, школьник сможет решить любую задачу

Перед отбором задач учителю необходимо

Слайд 9 1 Аналитический : анализ любой задачи позволяет вычленить

1 Аналитический : анализ любой задачи позволяет вычленить из нее подзадачи2)

из нее подзадачи

2) Основан на умениях, которые должны быть

сформированы у учеников после изучения темы.

3)Метод исключения и дополнения (Задача А – ключевая)

4) Основан на методах решения, которые учитель должен ввести и отработать в изучаемой теме

Методы отбора ключевых задач

А

В

А

Слайд 10
начинать лучше с самых простых ключевых задач;

задачи,

начинать лучше с самых простых ключевых задач; задачи, выходящие за рамки

выходящие за рамки школьной программы, лучше разбирать в конце

урока;

cамые яркие задачи лучше отнести на вторую часть урока;

Последовательность задач, разбираемых на уроке

Слайд 11
желательно чередовать задачи с обширными записями и те,

желательно чередовать задачи с обширными записями и те, которые не предполагают

которые не предполагают громоздких обоснований;

задачи, связанные с предыдущей

темой, лучше включать в число первых, а активно используемые в последующих темах - позднее

Последовательность задач, разбираемых на уроке

Слайд 12 умение школьников распознавать ключевые задачи;
умение решать ключевые

умение школьников распознавать ключевые задачи;умение решать ключевые задачи;умение правильно оформлять

задачи;
умение правильно оформлять решение ключевых задач;
умение запоминать такие

задачи, иметь их в своем арсенале;
умение осуществлять самоконтроль деятельности по решению ключевых задач.


Контролю усвоения ключевых задач подлежит

Слайд 13 Специальные уроки
Ознакомление учащихся с решением указанных задач

Специальные уроки Ознакомление учащихся с решением указанных задач Систематизации методов решения


Систематизации методов решения задач по теме
Решение задач, сводящихся

к последовательности ключевых

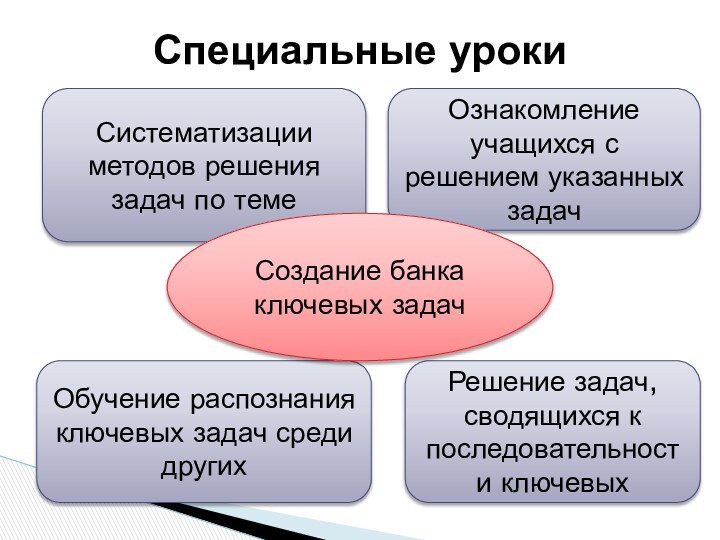
Обучение распознания ключевых задач среди других

Создание банка ключевых задач

Слайд 14 Ключевые задачи

Ключевые задачи

Слайд 15 1. Медианы в треугольнике пересекаются в одной точке

1. Медианы в треугольнике пересекаются в одной точке и делятся в

и делятся в ней в отношении 2:1, считая от

вершины.

2. Медиана делит треугольник на два равновеликих.

3. Медианы треугольника делят его на шесть равновеликих треугольников.

4. Если О – точка пересечения медиан треугольника АВС, то SАВС = 3SАОВ = 3SВОС
 

Свойства медиан треугольника.

Слайд 16 1 Сумма квадратов медиан треугольника равна суммы квадратов

1 Сумма квадратов медиан треугольника равна суммы квадратов его сторон.2. Сумма

его сторон.

2. Сумма квадратов медиан прямоугольного треугольника, проведенных из

вершин острых углов, равна квадрата его гипотенузы.

3. В прямоугольном треугольнике длина медианы, проведенной к гипотенузе, равна ее половине.

Длина медианы

Слайд 17

Ключевая задача. Докажите, что в прямоугольном треугольнике медиана,

Ключевая задача. Докажите, что в прямоугольном треугольнике медиана, проведенная к гипотенузе,

проведенная к гипотенузе, равна ее половине.


Медиана,

проведенная к гипотенузе.

Слайд 18
1. Центр описанной около

1. Центр описанной около прямоугольного треугольника окружности лежит на

прямоугольного треугольника окружности лежит на середине гипотенузы.

2. Если в

треугольнике длина медианы равна половине длины стороны, к которой она проведена, то этот треугольник – прямоугольный.

Следствия:

Слайд 19 А
С
B
M
A
D
C
B

АСBMADCB

Слайд 20 1. Найдите отношение суммы квадратов длин всех медиан

1. Найдите отношение суммы квадратов длин всех медиан треугольника к сумме

треугольника к сумме квадратов длин всех его сторон.

2. В

равнобедренном прямоугольном треугольнике медиана, проведенная к катету, равна l. Найдите площадь треугольника.

3. В равнобедренном треугольнике к боковой стороне, равной 4, проведена медиана, равная 3. Найдите основание треугольника.


Задачи системы.

Слайд 21 Задачи системы.

Задачи системы.

Слайд 22 Задачи на применение ключевой задачи

Задачи на применение ключевой задачи

Слайд 23 Ключевая задача «Свойства биссектрисы угла треугольника»

Ключевая задача «Свойства биссектрисы угла треугольника»

Слайд 24
Расстояние от вершины прямого угла до гипотенузы равно

Расстояние от вершины прямого угла до гипотенузы равно а, а до

а, а до точки пересечения биссектрисы меньшего угла с

меньшим катетом равно b. Найдите длину меньшего катета

Задача на применение ключевой:

Слайд 25 1. В треугольнике АВС С= 90°, СD –

1. В треугольнике АВС С= 90°, СD – биссектриса, AD=m, BD=n

биссектриса, AD=m, BD=n Найдите катеты треугольника.

2.В прямоугольный треугольник

вписана полуокружность так, что диаметр лежит на гипотенузе, а центр делит гипотенузу на отрезки длиной 15 и 20. Найдите радиус полуокружности.

3.Точка на гипотенузе, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 и 40. Найдите катеты треугольника

Упражнения на распознавание ключевой задачи

Слайд 26 4. В прямоугольный треугольник с углом 60°

4. В прямоугольный треугольник с углом 60° вписан ромб со

вписан ромб со стороной, равной 6, так, что угол

в 60° у них общий и все вершины ромба лежат на сторонах треугольника. Найдите стороны треугольника.

5. В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 и 20. Найдите биссектрису угла при основании треугольника.

Упражнения на распознавание ключевой задачи

Слайд 27
1. Концы лестницы скользят по стенкам угла. Какую

1. Концы лестницы скользят по стенкам угла. Какую траекторию описывает при

траекторию описывает при этом фонарик, находящийся на средней ступеньке

лестницы?

2. В прямоугольном треугольнике ABC ( C=900) CM - медиана. В треугольник BMC вписана окружность, точка касания делит отрезок BM пополам. Найдите острые углы треугольника ABC.

3. В равнобедренном треугольнике ABC основание AC равно 12. Точка M - середина BC, BK ⊥ AC и BK=MK. Найдите площадь треугольника.

4. В трапеции ABCD AB =2CD =2AD, AC=a, BC=b. Найдите основания AB и CD.

Задачи системы.

Слайд 28 Свойства треугольника, образованного основаниями высот данного остроугольного треугольника.

Свойства треугольника, образованного основаниями высот данного остроугольного треугольника.

Слайд 29 Задачи системы.

Задачи системы.

Слайд 30

Ключевая задача. Середины сторон произвольного четырехугольника являются вершинами

Ключевая задача. Середины сторон произвольного четырехугольника являются вершинами параллелограмма.  Свойства

параллелограмма.
 

Свойства четырехугольника, вершины которого являются серединами сторон данного

четырехугольника.

Слайд 31 Следствия.

Следствия.

Слайд 32 1. Докажите, что медианы треугольника пересекаются в одной

1. Докажите, что медианы треугольника пересекаются в одной точке и она

точке и она делит каждую медиану в отношении 2

: 1, считая от вершины.

2. Диагонали трапеции взаимно перпендикулярны, длина одной из них равна 6. Длина отрезка, соединяющего середины оснований, равна 5. Найдите площадь трапеции.


Задачи системы.

Слайд 33






Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

Ключевые

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Ключевые задачи по теме «параллелограмм»

задачи по теме «параллелограмм»

Слайд 34 Ключевые задачи по теме «параллелограмм»




Биссектрисы смежных углов параллелограмма

Ключевые задачи по теме «параллелограмм»Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.

пересекаются под прямым углом.






Слайд 35 Ключевые задачи по теме «параллелограмм»





Биссектрисы противоположных углов параллелограмма

Ключевые задачи по теме «параллелограмм»Биссектрисы противоположных углов параллелограмма параллельны

параллельны









Слайд 36 Ключевые задачи по теме «параллелограмм»






Высоты параллелограмма, опущенные из

Ключевые задачи по теме «параллелограмм»Высоты параллелограмма, опущенные из одной вершины, образуют

одной вершины, образуют угол, равный углу при соседней вершине

параллелограмма.









Слайд 37 Ключевые задачи по теме «параллелограмм»






Любой отрезок с концами

Ключевые задачи по теме «параллелограмм»Любой отрезок с концами на сторонах параллелограмма,

на сторонах параллелограмма, проходящий через его центр, делится центром

пополам.









Слайд 38


1) AOD подобен СOВ, k=a/b(коэффициент подобия равен отношению

1) AOD подобен СOВ, k=a/b(коэффициент подобия равен отношению оснований трапеции) 2)S1

оснований трапеции) 2)S1 = S2 (SABO = SDOC)

Ключевые задачи по

теме «трапеция»

Слайд 39 Рис. 2. В равнобокой трапеции Рис. 2 а. –

Рис. 2. В равнобокой трапеции Рис. 2 а. – углы при

углы при основании равны ( 1= 2)
Рис. 2 б.

– диагонали равны (d1=d2)
Рис. 2 в. - AOD – равнобедренный
Рис. 2 г. – если BL AD, CM AD, то ABL = DCM,
AL = MD = (a-b)/2
Рис. 2 д. – если BL AD, CM AD, то AM = LD = l (l – средняя линия.)

Слайд 40 Если в равнобокую трапецию вписана окружность, то ее

Если в равнобокую трапецию вписана окружность, то ее боковая сторона равна

боковая сторона равна средней линии трапеции. AB = CD =

(a+b)/2 = l

Слайд 41 1) Если трапеция равнобокая, то около нее можно

1) Если трапеция равнобокая, то около нее можно описать окружность. 2)

описать окружность. 2) Если около трапеции можно описать окружность, то

она равнобокая. Радиус окружности, описанной около трапеции ABCD, равен радиусу окружности, описанной около треугольника ABD, (или около треугольника, вершинами которого являются любые три вершины трапеции) R=abc/4S .

Слайд 42 Если окружность вписана в трапецию, то 1) суммы противоположных

Если окружность вписана в трапецию, то 1) суммы противоположных сторон трапеции

сторон трапеции равны AB + CD = AD + BC 2)

центр окружности – точка пересечения биссектрис, проведенных из углов, прилежащих к одной боковой стороне трапеции (AO; BO – биссектрисы) 3 BOA = 90° 4)Высота трапеции равна удвоенному радиусу вписанной окружности h=2r

Слайд 43
«Обучение математике имеет смысл только тогда, когда оно

«Обучение математике имеет смысл только тогда, когда оно учит думать, решать

учит думать, решать задачи. Способность решать задачи гораздо важнее,

чем просто владение информацией».

  • Имя файла: klyuchevye-zadachi-v-protsesse-obucheniya-shkolnikov-resheniyu-zadach-po-geometrii.pptx
  • Количество просмотров: 226
  • Количество скачиваний: 0
- Предыдущая Устная и письменная нумерация чисел в пределах 1000
Следующая - Особенности социально-экономического развития Индии

Похожие презентации

Презентация викторина Твоя профессия Презентация викторина Твоя профессия 138
300 let tsarskomu selu - 1 300 let tsarskomu selu - 1 125
Духовно-нравственное воспитание педсовет Духовно-нравственное воспитание педсовет 95
Презентация Морская артикуляционная гимнастика презентация к уроку по логопедии (подготовительная группа) Презентация Морская артикуляционная гимнастика презентация к уроку по логопедии (подготовительная группа) 117
Презентация к открытому классному часу Международный день родного языка (6 класс) Презентация к открытому классному часу Международный день родного языка (6 класс) 169
Презентация педсовета Дополнительное образование как средство реализации внеурочной деятельности. Проблемы. Перспективы Презентация педсовета Дополнительное образование как средство реализации внеурочной деятельности. Проблемы. Перспективы 168
Развитие навыка чтения у ребенка Развитие навыка чтения у ребенка 93
Методы работы с одарёнными детьми Методы работы с одарёнными детьми 115
Новое в УМК: Enjoy English Новое в УМК: Enjoy English 97
Правонарушение. Преступление. Ответственность (6 класс) Правонарушение. Преступление. Ответственность (6 класс) 140
Новый федеральный порядок аттестации в 2011 аттестационном году Новый федеральный порядок аттестации в 2011 аттестационном году 94
Классный час Моё здоровье в моих руках. классный час (2 класс) Классный час Моё здоровье в моих руках. классный час (2 класс) 146
Презентация к докладу Дети группы риска - психологический аспект Презентация к докладу Дети группы риска - психологический аспект 120
Конфликты с собственным ребёнком и пути их разрешения Конфликты с собственным ребёнком и пути их разрешения 90
банкіри банкіри 99
Презентация Неделя науки в КБР Презентация Неделя науки в КБР 118
Виртуальная экскурсия Виртуальная экскурсия 96
Применение методов театральной педагогики в учебно-воспитательной работе начальной школы методическая разработка (2 класс) по теме Применение методов театральной педагогики в учебно-воспитательной работе начальной школы методическая разработка (2 класс) по теме 120
Классный час Здравствуй, 3 класс классный час (3 класс) по теме Приходите в 3 класс! Классный час Здравствуй, 3 класс классный час (3 класс) по теме Приходите в 3 класс! 123
Проектная деятельность учащихся Проектная деятельность учащихся 102
Презентация по ИЗО на тему Волшебный лес Презентация по ИЗО на тему Волшебный лес 105
ЗОЖ план-конспект занятия (3 класс) ЗОЖ план-конспект занятия (3 класс) 60
Содержание методического кабинета ДОУ Содержание методического кабинета ДОУ 99
Урок здоровья Здоровое питание-отличное настроение презентация к уроку (3 класс) Урок здоровья Здоровое питание-отличное настроение презентация к уроку (3 класс) 116
Полководцы и герои войны 1812 года презентация к уроку (2 класс) по теме Полководцы и герои войны 1812 года презентация к уроку (2 класс) по теме 121
Презентация на родительское собрание: Цена времени Презентация на родительское собрание: Цена времени 131
Критерии здоровьесбережения на уроке. учебно-методический материал по теме Критерии здоровьесбережения на уроке. учебно-методический материал по теме 122
Нравственно – патриотическое воспитание через приобщение к хозяйственно-бытовому труду старших дошкольников Нравственно – патриотическое воспитание через приобщение к хозяйственно-бытовому труду старших дошкольников 94
Проект Ох, уж эти буквы! презентация к уроку по логопедии (подготовительная группа) Проект Ох, уж эти буквы! презентация к уроку по логопедии (подготовительная группа) 47
Должностная инструкция педагога-психолога в процессе внедрения профессионального стандарта педагога-психолога методическая разработка Должностная инструкция педагога-психолога в процессе внедрения профессионального стандарта педагога-психолога методическая разработка 108