Презентация на тему Достовірність різниць середніх і перевірка зв'язку між змінними лекції

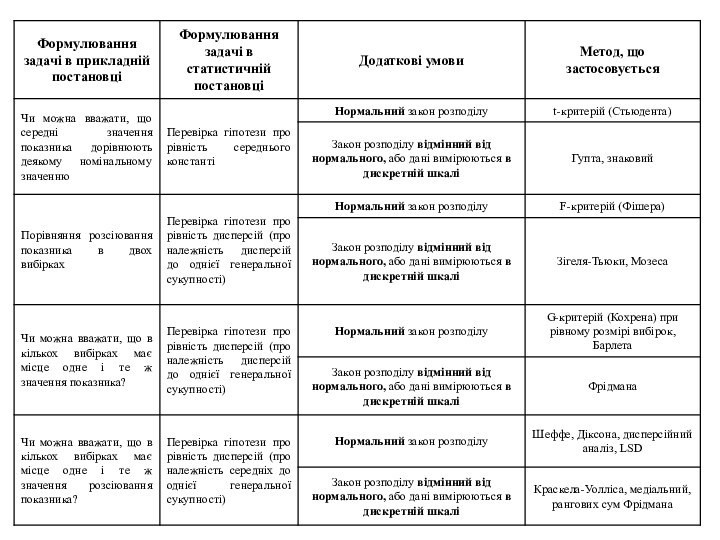
Бартлета.
Критерій знаків.
Критерій Зігеля-Тьюкі.
Критерій Кракскела-Уоліса.
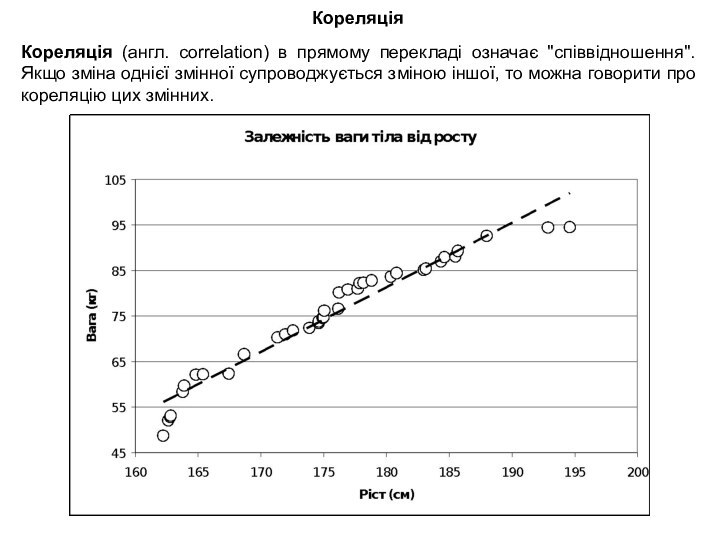
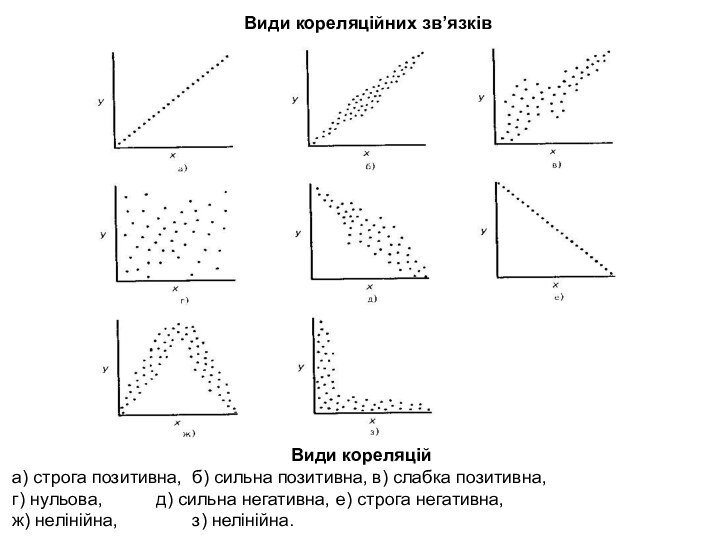
Коефіцієнт кореляції Кендала.
Конкордація Кендала.
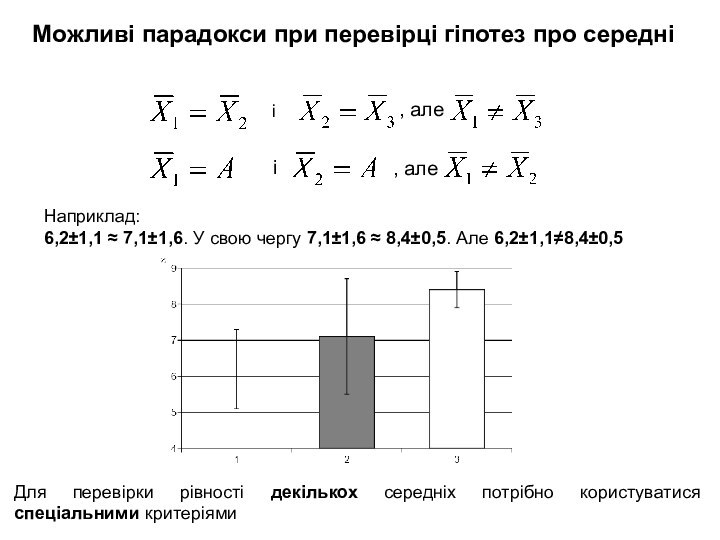
Перевірка рівності декількох

середніх та фактору впливу на змінні методом дисперсійного аналізу.
Таблиці спряження.

називаються такі методи дослідження, у яких усі дані, що

входять до вибірок чи генеральних сукупностей попадають під закон нормального розподілу.

При параметричних методах дослідження оперують та порівнюють між собою, в основному, показники дисперсій (або середньоквадратичних відхилень) та середньоарифметичні значення (також використовують інші середні величини: геометричні, гармонійні, квадратичні та кубічні).

або на початку більшу дисперсію ділять на меншу, або

якщо результат уже відомий і він менший від одиниці (наприклад 0,843), то одиницю ділять на результат (в нашому випадку 1/0,843).

Критичне значення критерію Фішера перевіряють за спеціальними таблицями. Причому для перевірки беруться ступені вільності чисельника і знаменника окремо (nчис-1, nзнам-1).
Якщо розрахункове (емпіричне) значення критерію Фішера (при заданому ступені вірогідності ) більше за табличне (критичне), то дисперсії різні.

t-критерій Стьюдента для незалежних вибірок, то потрібно, щоб дисперсії

були рівними.
Потрібно враховувати розмір та співвідношення розмірів вибірок.

Випадки, які потрібно враховувати:
Об’єм вибірки
обидві групи великі (n>30)
обидві групи малі (n<30)
одна група велика, інша – мала
За складом
вибірки залежні
вибірки незалежні
Критерій стійкий і при малих відхиленнях від нормального розподілу

2-х великих, або великої та малої вибірок:
або
де:
та
- середні арифметичні

1-ї та 2-ї вибірок

- дисперсії 1-ї та 2-ї вибірок

та

- похибки середніх арифметичних 1-ї та 2-ї вибірок

та

та

- об’єми 1-ї та 2-ї вибірок

Критичне значення t-критерію Стьюдента перевіряють за спеціальними таблицями. Для перевірки беруться ступені вільності, які розраховуються за формулою:
k=n1+n2-2, або k=n1-1+n2-1.
Якщо розрахункове (емпіричне) значення t-критерію Стьюдента (при заданому ступені вірогідності ) більше за табличне (критичне) то середні різні.

2-ї вибірок
- дисперсії 1-ї та 2-ї вибірок
та
та
- об’єми 1-ї

та 2-ї вибірок

Критичне значення t-критерію Стьюдента перевіряють за спеціальними таблицями. Для перевірки беруться ступені вільності, які розраховуються за формулою:
k=n1+n2-2, або k=n1-1+n2-1.
Якщо розрахункове (емпіричне) значення t-критерію Стьюдента (при заданому ступені вірогідності ) більше за табличне (критичне) то середні різні.

досить точний і може застосовуватися як для великих так

і малих за розміром вибірок

та

- середні арифметичні 1-ї та 2-ї вибірок

- дисперсії 1-ї та 2-ї вибірок

та

та

- об’єми 1-ї та 2-ї вибірок

де:

Критичне значення t-критерію Стьюдента перевіряють за спеціальними таблицями. Для перевірки беруться ступені вільності, які розраховуються за формулою:
k=n1+n2-2, або k=n1-1+n2-1 .
Якщо розрахункове (емпіричне) значення t-критерію Стьюдента (при заданому ступені вірогідності ) більше за табличне (критичне) то середні різні.

даний вид порівняння середніх має лише наближене вирішення і

в математиці називається проблемою Беренса-Фішера.
Можна наближено застосувати формулу (як і для рівних дисперсій):

де:

та

- середні арифметичні 1-ї та 2-ї вибірок

- дисперсії 1-ї та 2-ї вибірок

та

- похибки середніх арифметичних 1-ї та 2-ї вибірок

та

та

- об’єми 1-ї та 2-ї вибірок

або

закон нормального розподілу і їх потрібно порівняти із якоюсь

стандартною величиною, то використовують наступну формулу:

де:

- середнє арифметичне вибірки

- дисперсія вибірки

Критичне значення t-критерію Стьюдента перевіряють за спеціальними таблицями. Для перевірки беруться ступені вільності вибірки, якій розраховується за формулою:
k=n-1.
Якщо розрахункове (емпіричне) значення t-критерію Стьюдента (при заданому ступені вірогідності ) більше за табличне (критичне) то середні різні.

- величина з якою порівнюється середнє арифметичне вибірки

ступені вільності обрахуємо за формулою:
k=n1+n2-2

Тобто

, а k=38+36-2=72

За таблицею для даних ступенів вільності критичне значення буде:
tкр.(0,05; 37; 35)=1,99.

Оскільки розрахункове значення (емпіричне) менше за критичне (табличне), тобто tрозр.

і
, але
і
, але
Для перевірки

рівності декількох середніх потрібно користуватися спеціальними критеріями

Наприклад:
6,2±1,1  7,1±1,6. У свою чергу 7,1±1,6  8,4±0,5. Але 6,2±1,18,4±0,5

ранжування
Ранг – це той номер значення у варіаційному ряду,

який би воно (значення) отримало, якби ці значення були відсортовані (розставлені) по порядку.

Наприклад
Є ряд даних:
34, 17, 25, 43, 15, 26, 14, 20

Відсортуємо їх у порядку зростання
14, 15, 17, 20, 25, 26, 34, 43

Пронумеруємо ці дані у порядку зростання:
14, 15, 17, 20, 25, 26, 34, 43
1 2 3 4 5 6 7 8

Отримані номера (з 1 по 8 ) і будуть називатися рангами, а сам процес їх встановлення – ранжуванням.

Часто ранги можна і не визначати, а скористатися готовими експериментальними даними, якщо ці дані являють собою цілі числа і їх розмах однаковий для всіх порівнювальних груп.
Це можуть бути шкільні оцінки, суддівські бали, кількість вистрелів і т.п.

нараховується ранг 1. Найбільшому значенню нараховується ранг, що відповідає

кількості значень, які ранжуються.
Наприклад, якщо n=7, то найбільше значення отримає ранг 7, за можливим виключенням для тих випадків, які передбачені правилом 2.
У разі, якщо декілька значень рівні, їм нараховується ранг, що є середнім значенням з тих рангів, які вони отримали б, якби не були рівні. Наприклад, 3 найменші значення дорівнюють 10 секундам. Якби ми вимірювали час точніше, то ці значення могли б розрізнятися і складали б, скажімо, 10,2 с; 10,5 с; 10,7 с. В цьому випадку вони отримали б ранги, відповідно, 1, 2 і 3. Але оскільки отримані нами значення рівні, кожне з них отримує середній ранг: (1 + 2 + 3)/3 = 6/3 = 2. Допустимо, наступні 2 значення дорівнюють 12 сек. Вони повинні були б отримати ранги 4 і 5, але, оскільки вони рівні, то отримують середній ранг: (4 + 5) / 2 = 4,5
3. Загальна сума рангів повинна співпадати з розрахунковою, яка визначається по формулі: рангів = (n²+n)/2,
де n - загальна кількість спостережень (значень), що ранжуються.
Неспівпадання реальної і розрахункової сум рангів свідчить про помилку, допущену при нарахуванні рангів або їх підсумовуванні.

переважно у залежних вибірках, коли немає відомостей про рівність

дисперсій.

Вимоги:
Шкала вимірювання повинна бути порядковою, інтервальною або відносною (тобто критерій не можна застосовувати до номінальних змінних).
Досліджувані значення повинні бути неперервними і симетричними відносно своєї медіани
Кількість значень для аналізу повинна бути не менше 5.

Послідовність виконання розрахунків:
Скласти список досліджуваних вимірів у будь-якому порядку, наприклад алфавітному (повинно вийти 2 стовпчика: до дослідження та після).
Вирахувати різницю між індивідуальними значеннями у другому і першому вимірюваннях («після» - «до»). Якщо в різниця рівна 0, то її до уваги не беруть.
Проранжувати ці дані не звертаючи уваги на знаки (по модулю).
Просумувати ранги окремо для позитивних і негативних різниць.
Яка сума буде меншою, ту й вважають емпіричним (експериментальним) критерієм Уілкоксона.
Якщо емпіричне значення більше критичного (табличного) то різниця недостовірна.

при кульовій стрільбі. Обстежувані стріляли в сонячну погоду і,

наступного дня, в похмуру. Дані занесено в таблицю:

Чи можна вважати, що дані у сонячну погоду відрізнялися від даних отриманих у похмуру?

Розв’язок.
Нульова гіпотеза: Різниць немає.
Розраховуємо різницю між окремими показниками в сонячну погоду та, відповідно, похмуру.

за різницею від найменшого до найбільшого без врахування знаку

(по модулю)

рангів для позитивних і негативних значень
W+=1+2+4=7, W-=4+4+6+7=21
6. Для порівняння

беремо менше із значень сум рангів. В даному випадку це 7

7. Перевіряємо його із табличним (критичним значенням). Для нашого випадку для 7 значень критичне значення буде рівне 2.

8. Відповідь. Оскільки емпіричне (розрахункове, експериментальне) значення більше за табличне (критичне), то нульова гіпотеза приймається, тобто середні значення у двох вибірках суттєво не відрізняються.

вибірках, коли немає відомостей про рівність дисперсій. Вважається найпотужнішим

із непараметричних критеріїв.
Вимоги:
Шкала вимірювання повинна бути порядковою, інтервальною або відносною (тобто критерій не можна застосовувати до номінальних змінних).
Досліджувані значення повинні бути повинні бути неперервними і симетричними відносно своєї медіани
Кількість значень для аналізу у меншій вибірці повинна бути не менше 5.

Послідовність виконання розрахунків:
Скласти список досліджуваних вимірів у будь-якому порядку в один ряд або стовпчик наприклад алфавітному (повинно вийти 2 стовпчика).
Об’єднати 2 стовпчика в один.
Відсортувати дані у стовпчику за зростанням.
Проранжувати ці дані.
Провести розрахунки за формулами:
де R1 і R2 - суми рангів, розрахованих для значень, які належать першій і другій вибіркам відповідно, n1 і n2 – об’єми першої та другої вибірок.
Яке значення U1 чи U2 буде меншим, те значення вважають емпіричним (експериментальним) критерієм Манна-Уітні.
Якщо емпіричне значення більше критичного (табличного) то різниця недостовірна.

Критерій Манна-Уітні (U-критерій, Уілкоксона-Манна-Уітні)

U1=n1n2+0,5n1(n1+1)-R1 , U2=n1n2+0,5n2(n2+1)-R2

секундах) у хлопців-баскетболістів та хлопців-футболістів. Дані занесено в таблицю:
Чи

можна вважати, що середні значення між баскетболістами і футболістами відрізнялися?

Розв’язок.
Нульова гіпотеза: Різниць немає.
Об’єднуємо дані в одну спільну вибірку.

2. Відсортовуємо дані за зростанням

3. Присвоюємо даним відповідні ранги

з першої та другої вибірок.
R1=2+3,5+3,5+6+7+11+12+13+14=72
R2=1+5+8+9,5+9,5+15+16=64
Для порівняння беремо менше із

значень U1 чи U2. В нашому випадку це 27.

6. Перевіряємо його із табличним (критичним даним). Для нашого випадку для 9 та 7 значень критичне значення буде рівне 12.

7. Відповідь. Оскільки емпіричне (розрахункове, експериментальне) значення більше за табличне (критичне), то нульова гіпотеза приймається, тобто середні значення у двох вибірках суттєво не відрізняються.

Якщо зміна однієї змінної супроводжується зміною іншої, то можна

говорити про кореляцію цих змінних.

Кореляція

слабка позитивна,
г) нульова, д) сильна негативна, е) строга негативна,
ж) нелінійна, з)

нелінійна.

-1 до 1.
Якщо коефіцієнт кореляції зі знаком «-», то

кореляція негативна (від’ємна, мінусова, обернена), якщо зі знаком «+», то позитивна (додатна, плюсова, пряма).

Коефіцієнт кореляції часто показує лише на залежність величини X від велечини Y, але це не значить, що величина Y теж обов’язково буде залежати від величини X.

Кількість обстежуваних у обох вибірках повинна бути строго однакова. В противному випадку, або програма відмовиться рахувати, або недостаючі (порожні) дані будуть замінені нульовими значеннями, що призведе до значних викривлень у розрахунках.

Достовірність коефіцієнту кореляції залежить від об’єму вибірки. Чим більша за об’ємом вибірка, тим менше значення (за абсолютною величиною) коефіцієнту кореляції буде вважатися достовірним.

застосування.
Лише тоді коли дані в обох вибірках попадають під

закон нормального розподілу

Значення tкор перевіряється із табличним (критичним). Якщо розраховане (експериментальне) значення коефіцієнту кореляції більше за табличне (критичне), то така кореляція вважається достовірною.

а скільки завгодно;
ви можете не знати про всі впливаючі

змінні;
деякі автори стверджують, що для коректного використання приватного коефіцієнта кореляції необхідна наявність так званого багатомірного нормального закону розподілу

Кореляція між двома змінними, вирахувана після усунення впливу усіх інших змінних, називається приватною кореляцією.
Наприклад
Довжина волосся може корелювати з ростом людини (чим вища людина, тим коротше волосся), проте ця залежність стає слабкою або зовсім зникає, якщо усунути вплив статі спостережуваних людей, оскільки жінки зазвичай нижче ростом і частіше мають довше волосся, ніж чоловіки.

виміру;
Розподіл даних хоча б у одній вибірці занадто відрізняється

від нормального або взагалі невідомий;
Вибірки мають невеликий об'єм (n<30).

Перевіряється достовірність коефіцієнту кореляції Спірмена аналогічно як і коефіцієнт кореляції Пірсона за відповідними таблицями.

Якщо вибірки попадали під закон нормального розподілу (або мали незначне відхилення) то із коефіцієнту кореляції Спірмена можна розрахувати коефіцієнт кореляції Пірсона за формулою:

розгону (ознака X) від величини кінцевої швидкості розгону (ознака

Y).

Нульова гіпотеза: результат стрибка не залежить від швидкості розгону
Розв’язок
Даних мало. Отже під закон нормального розподілу вони не попадуть.
Тому для встановлення залежності застосуємо коефіцієнт кореляції Спірмена.
1. Замінимо всі дані на їхні ранги (проранжуємо дані за ознакою X та ознакою Y).

2. У відповідності до формули знайдемо квадрат різниці рангів.

Розраховуємо власне коефіцієнт кореляції Спірмена:
5. Перевіряємо достовірність

розрахованого нами коефіцієнту кореляції.
Табличне значення для 8 досліджуваних 0,64.

6. Відповідь. Оскільки емпіричне (розрахункове, експериментальне) значення більше за табличне (критичне), то нульова гіпотеза відкидається (не приймається), тобто результат стрибка в довжину з розгону залежить від величини кінцевої швидкості розгону

досліджувані дані або показники попадають під закон нормального розподілу.
У

випадку коли є сумніви, що до відповідності розподілу даних за законом нормального розподілу, то в такому разі доцільніше використовувати непараметричні (рангові) методи аналізу даних.
Усі непараметричні методи аналізу базуються на перетворенні досліджуваних величин у рангові показники.

розподілу вибірок

[1] В ряді випадків фактично перевіряється гіпотеза про

рівність медіан або обох мір положення

[1] В ряді випадків фактично перевіряється гіпотеза про рівність медіан або обох мір положення