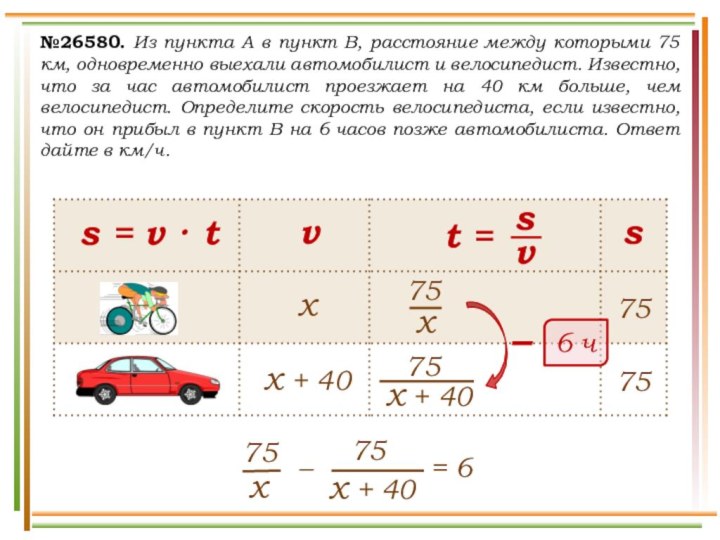
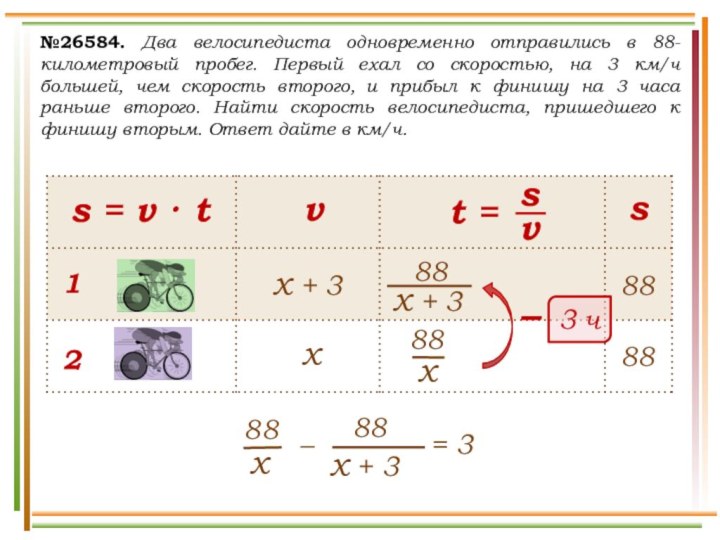
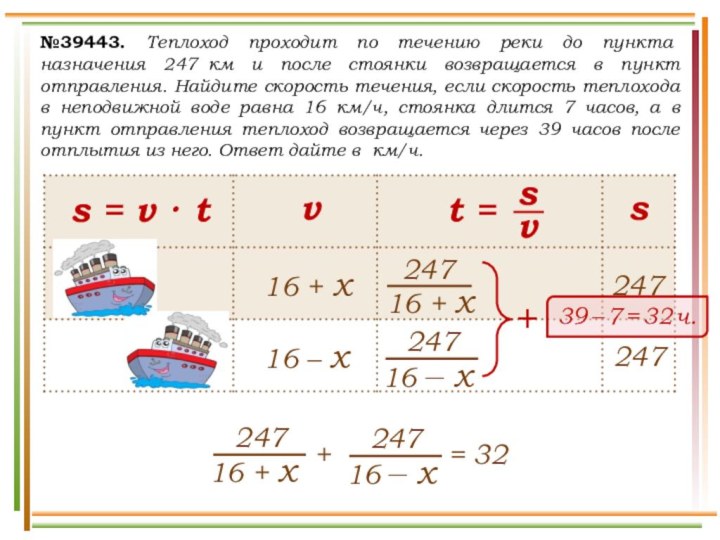
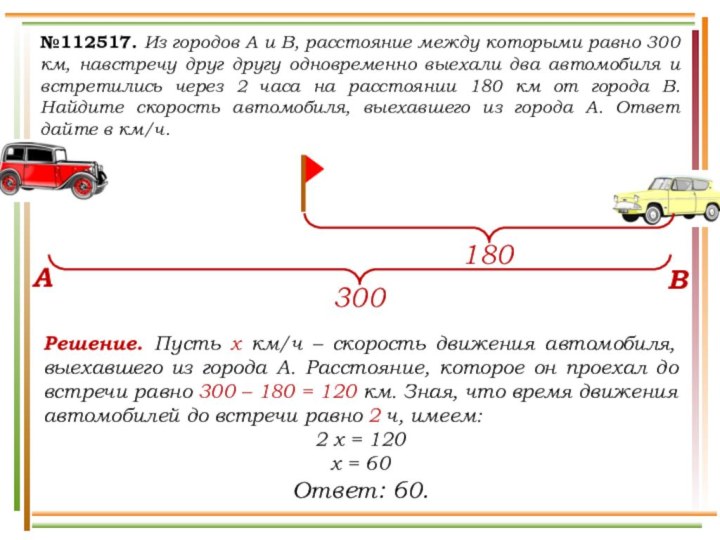
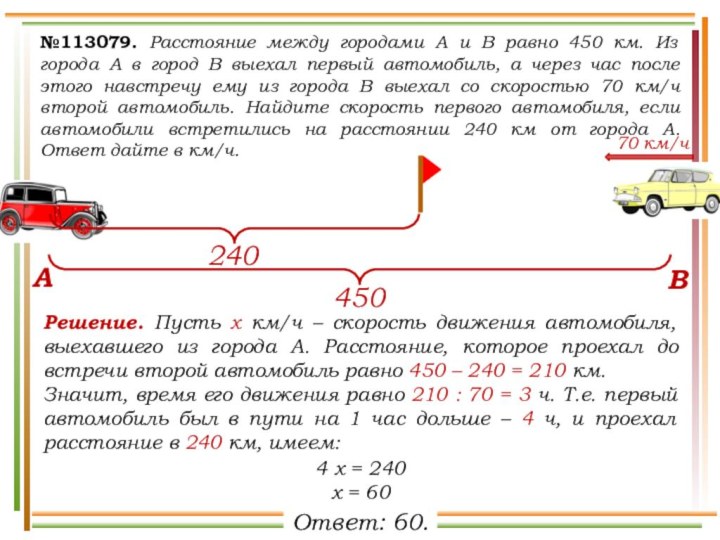
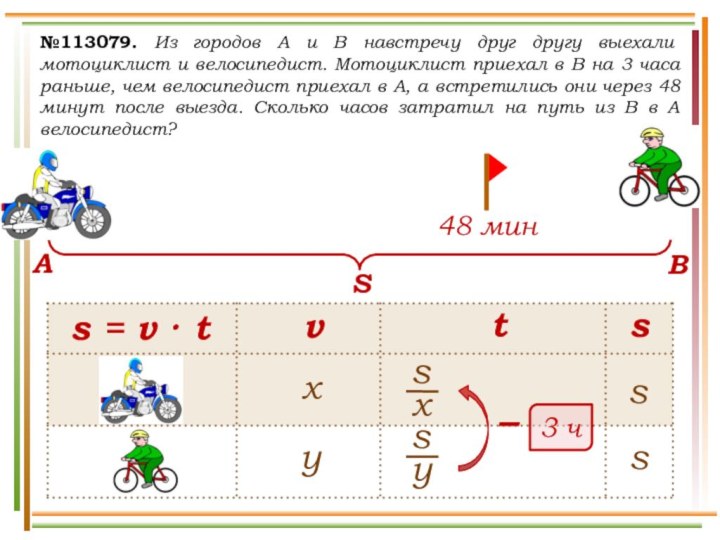
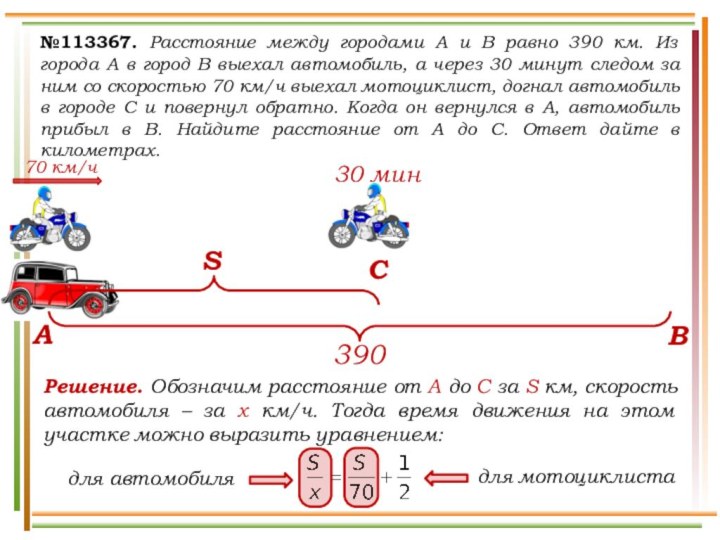
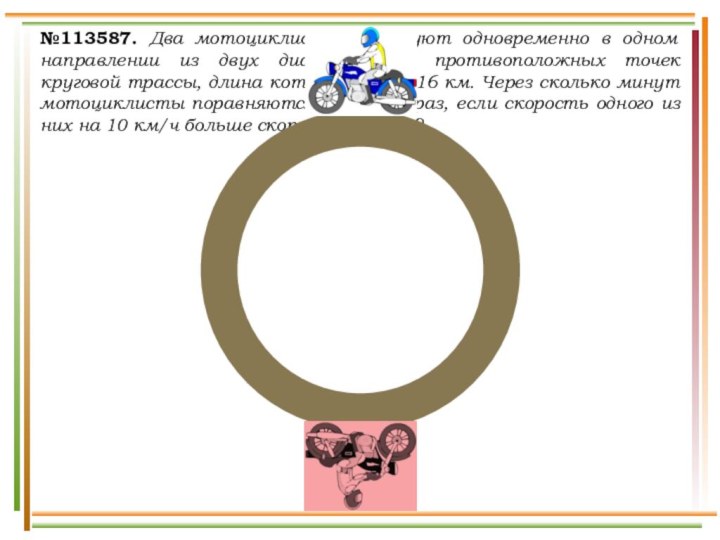
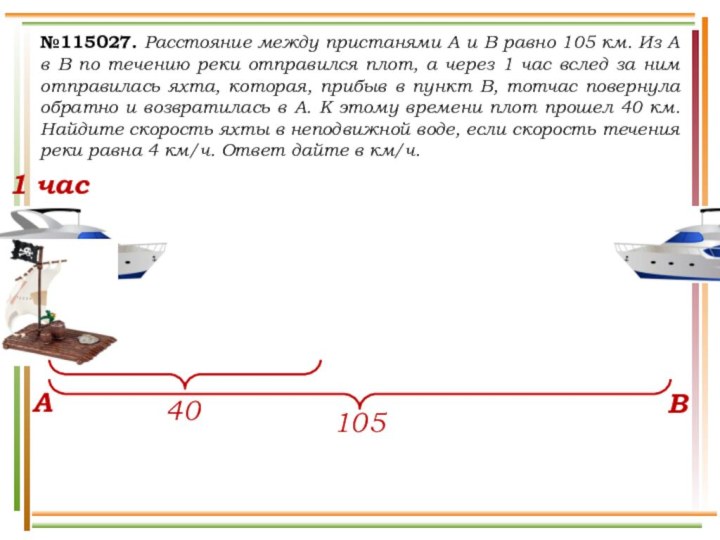
выехали два автомобиля. Первый проехал с постоянной скоростью весь
путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.v
s
1
2
х
s
s
1) 24
2) х + 16
s = v · t
=