Слайд 2
Quicksort (рекурсивен, как и Mergesort)
Основная идея:
Перетасовываем массив
Разделяем его
так, что для любой j
Элемент a[j] находится на правильном
месте в массиве
Слева от j нет большего элемента
Справа от j нет меньшего элемента
Сортируем каждый участок рекурсивно
И т.д. – рекурсивно сортируем левые и правые части
Слайд 3
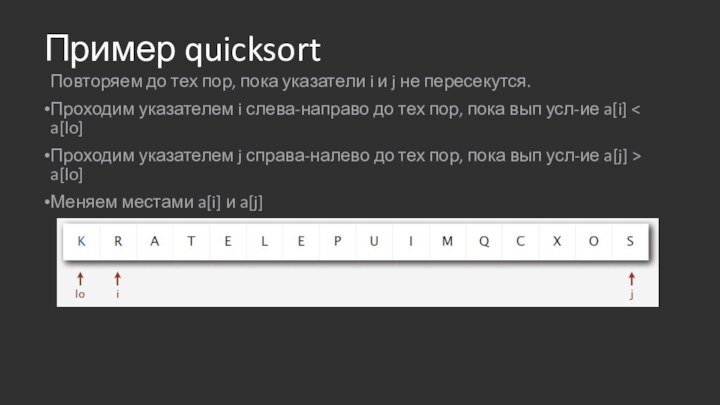
Пример quicksort
Повторяем до тех пор, пока указатели i
и j не пересекутся.
Проходим указателем i слева-направо до тех
пор, пока вып усл-ие a[i] < a[lo]
Проходим указателем j справа-налево до тех пор, пока вып усл-ие a[j] > a[lo]
Меняем местами a[i] и a[j]
Слайд 4
Пример quicksort
Выбираем K в качестве разделителя.
Двигаем указатель
i слева-направо, до тех пор пока не найдем элемент,
больший чем разделитель K.
И двигаем указатель j справа-налево, пока не найдем элемент меньший разделителя K.
В данном примере:
i останавливается сразу, так как K > R и условие a[i]
Слайд 5
Пример quicksort
Выбираем K в качестве разделителя.
Двигаем указатель
i слева-направо, до тех пор пока не найдем элемент,
больший чем разделитель K.
И двигаем указатель j справа-налево, пока не найдем элемент меньший разделителя K.
В данном примере:
j останавливается в C, так как C < K и условие a[j]>a[lo] не выполняется
Слайд 6
Пример quicksort
Мы нашли позиции a[i] и a[j], удовлетворяющие
условиям относительно a[lo].
Меняем a[i] и a[j] местами
Слайд 7
Пример quicksort
Меняем стартовые позиции - i увеличиваем на
1 и j уменьшаем на 1
Слайд 8
Пример quicksort
Ищем a[i] и a[j], удовлетворяющие условиям.
Это a[i]
= T и a[j] = I
Слайд 9
Пример quicksort
Меняем их местами
Слайд 10
Пример quicksort
Продолжаем по аналогии
Меняем местами
Слайд 11
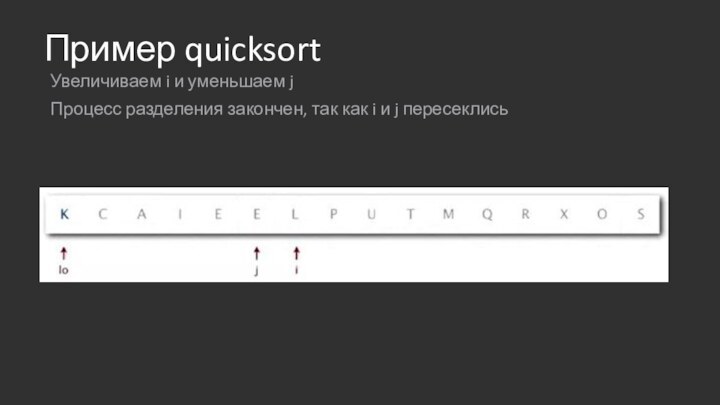
Пример quicksort
Увеличиваем i и уменьшаем j
Процесс разделения закончен,
так как i и j пересеклись
Слайд 12
Пример quicksort
Фаза 2 (указатели пересеклись)
Меняем местами a[lo] и
a[j]
Теперь слева от K только меньшие элементы, в справа
только большие
Слайд 13
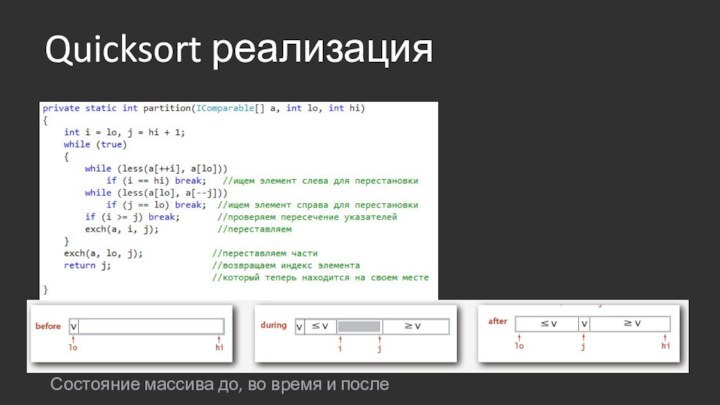
Quicksort реализация
Состояние массива до, во время и после
Слайд 14
Quicksort реализация
А перетасовывается для того, чтобы гарантировать нормальную
производительность
Слайд 16
Quicksort особенности реализации
Разделение. Использование дополнительного массива делает разделение
более простым и стабильным, но требует доп памяти.
Quicksort, в
отличии от Mergesort, использует только 1 массив.
Удаление циклов. Проверка пересечения указателей i и j, немного сложнее, чем кажется.
Остаемся в границах массива. Проверка j == lo не нужна, так как там есть разделитель (a[lo]), но i == hi нужна.
Сохранение случайности элементов. Перетасовка массива необходима для гарантии производительности.
Одинаковые ключи. Когда есть одинаковые элементы, лучше останавливаться на элементах, равных разделителю.
Слайд 17
Quicksort эмпирический анализ
Оценки производительности
Домашний ПК – 10^8 операций/сек
Суперкомпьютер
– 10^12 операций/сек
Слайд 18
Quicksort анализ в лучшем случае
Лучший случай. Число сравнений
~ N*lgN
Слайд 19
Quicksort анализ в худшем случае
Лучший случай. Число сравнений
~ ½ *N2
Если мы предварительно отсортируем массив, то такой
случай маловероятен.
Слайд 20
Quicksort. Анализ с среднестатистическом случае
Предположение. Среднее число сравнений
CN для сортировки quicksort массива N различных элементов ~
2*N*lnN (и число перестановок ~ 1/3*N*lnN)
Док-во. CN удовлетворяет рекуррентному соотношению C0 = C1 = 0 и N>=2:
Умножаем обе половины на N и раскрываем скобки:
(I)
Записываем (I) для N-1 и вычитаем его из (I), получаем:
Слайд 21
Quicksort. Анализ с среднестатистическом случае
Док-во. Переставляем слагаемые и
делим всё на N*(N+1)
Рекурсивно подставляем данное соотношение:
Слайд 22
Quicksort. Анализ с среднестатистическом случае
Док-во. Переставляем слагаемые и
делим всё на N*(N+1)
Рекурсивно подставляем данное соотношение:
Слайд 23
Quicksort. Анализ с среднестатистическом случае
Док-во. Вычисляем сумму с
помощью интеграла
Получаем желаемый результат:
Слайд 24
Quicksort. Выводы по производительности.
Худший случай. Число сравнений квадратично
1
Такой
случай маловероятен, из-за предварительной случайной перетасовки
Среднестатистический случай. Число сравнений
~ 1.39*N*lgN
На 39% больше сравнений чем в Mergesort
Но быстрее Mergesort из-за меньшей работы с памятью
Случайная сортировка.
Случайность спасает от худшего случая
Основа для мат модели, которая может быть оценена с помощью экспериментов.
Стоит учитывать что! Многие книжные реализации работают квадратично, если:
Массив отсортирован (по убыванию или возрастанию)
Имеет много повторяющихся элементов (даже если случайно перетасован)
Слайд 25
Quicksort. Свойства
Предположение. Quicksort сортирует «на месте», т.е. не
использует доп массивов.
Док-во. 1) Разделение. Требует фиксированной доп памяти
2)
Глубина рекурсии. Логарифмическая доп память (с высокой вероятностью)
Предположение. Quicksort нестабилен.
Док-во.
Слайд 26
Quicksort. Свойства
Предположение. Quicksort сортирует «на месте», т.е. не
использует доп массивов.
Док-во. 1) Разделение. Требует фиксированной доп памяти
2)
Глубина рекурсии. Логарифмическая доп память (с высокой вероятностью)
Предположение. Quicksort нестабилен.
Док-во. Разделение совершает
Перестановки на большие расстояния
Слайд 27
Quicksort. Возможные улучшения
Сортировка со вставкой для маленьких подмассивов
Quicksort
жрет слишком много памяти для маленьких массивов
Предел для использования
Quicksort – от 10 элементов
Java-code. For C# change Comparable[] to IComparable[]
Слайд 28
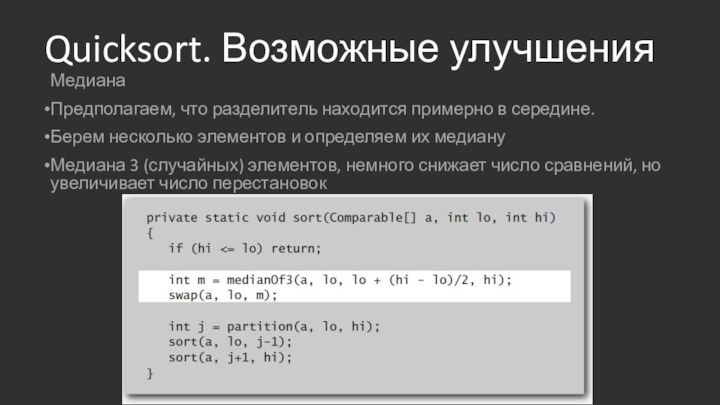
Quicksort. Возможные улучшения
Медиана
Предполагаем, что разделитель находится примерно в
середине.
Берем несколько элементов и определяем их медиану
Медиана 3 (случайных)
элементов, немного снижает число сравнений, но увеличивает число перестановок
Слайд 29
ПРОСЫПЕМСЯ!
Предполагаемое время работы алгоритма quicksort с случайной перетасовкой
на уже отсортированном массиве:
Линейно
N*lgN
Квадратично
Экспоненциально
Слайд 30
Выборка
Дан массив N элементов, найти k-ый наибольший элемент
Прим.
Минимум (k=0), максимум (k=N-1), медиана (k = N/2)
Приложения:
Статистика
Найти наибольшие
k элементов
Теоретические знания для реализации алгоритмва:
N*logN верхняя граница – сортируем массив, макс элт – последний, мин - первый
N верхняя граница для k=1,2,3 – если k мало, то время работы проп-но N
N нижняя граница – достаточно просмотреть весь массив
Из всего этого можно сделать вывод – нужен линейный алгоритм.
Существует ли линейный алгоритм или выборка так же сложна как сортировка.
Слайд 31
Quick-select. Быстрая выборка
Разделяем массив, так что:
a[j] находится на
месте
Слева от j нет больших элементов
Справа от j нет
меньших элементов
Повторяем в одном подмассиве, в зависимости от j; заканчиваем когда j равно k
Слайд 32
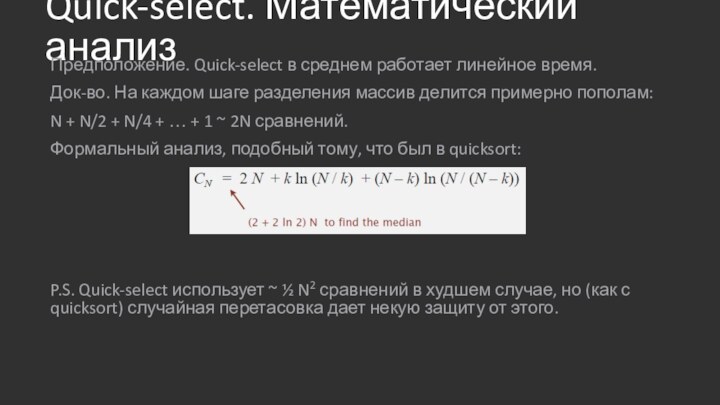
Quick-select. Математический анализ
Предположение. Quick-select в среднем работает линейное
время.
Док-во. На каждом шаге разделения массив делится примерно пополам:
N
+ N/2 + N/4 + … + 1 ~ 2N сравнений.
Формальный анализ, подобный тому, что был в quicksort:
P.S. Quick-select использует ~ ½ N2 сравнений в худшем случае, но (как с quicksort) случайная перетасовка дает некую защиту от этого.
Слайд 33
ПРОСЫПАЕМСЯ!!!
Каково ожидаемое время работы для поиска медианы используя
quick-select со случайной перетасовкой?
Постоянно
Логарифмично
Линейно
N*lgN
Слайд 34
Повторяющиеся ключи (элементы)
Часто, задачей сортировки является группировка записей
с одинаковыми ключами
Сортировка по возрасту
Удаление одинаковых писем из ящика
Прибытий
автобусов на остановки
Типичные свойства подобных приложений:
Большие массивы данных
Маленькое число ключей
Слайд 35
Повторяющиеся ключи
Mergesort для повторяющихся ключей. Число сравнений между
½*N*lgN и N*lgN
Quicksort для повторяющихся ключей:
Алгоритм квадратичен, но не
в случае когда разделение останавливается на одинаковых ключах!
Слайд 36
Повторяющиеся ключи. Проблема
Ошибка. Все элементы, равные разделителю, размещаются
с одной стороны
Последствие. ~ ½ N2 сравнений, если все
ключи одинаковы.
Рекомендуется. Останавливать поиск на элементах равных разделителю.
Последствие. ~N*lgN сравнений когда все ключи одинаковы.
Чего хотим. Размещать все элементы, равные разделителю, в одном месте.
Слайд 37
Разделение в 3 направлениях
Цель. Разделять массив на 3
части таким образом, что:
Элементы между lt и gt равны
разделителю v
Слева от lt нет больших элементов
Справа от gt нет меньших элементов
Слайд 38
Разделение в 3 направлениях. пример
Пусть v разделитель a[lo]
Сканируем
i cлева-направо.
(a[i] < v): меняем местами a[lt] и a[i];
увеличиваем lt и i
(a[i] > v): меняем местами a[gt] и a[i]; уменьшаем gt
(a[i] == v): увеличиваем i
Слайд 39
Разделение в 3 направлениях. пример
Указатель i находится слева
от неизвестной (не просмотренной области).
Слева от lt всё меньшее
v, между lt и i – равное v, между i и gt – неизвестное, больше gt – большее v
Слайд 40
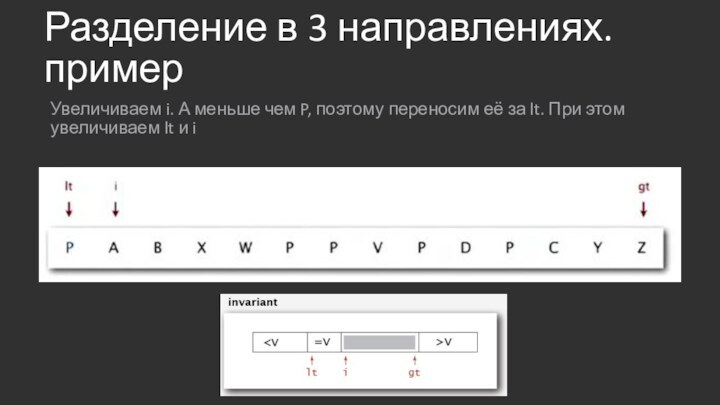
Разделение в 3 направлениях. пример
Увеличиваем i. А меньше
чем P, поэтому переносим её за lt. При этом
увеличиваем lt и i
Слайд 41
Разделение в 3 направлениях. пример
Теперь i указывает на
B, B тоже меньше чем P, переносим элемент. Увеличиваем
lt и i
Слайд 42
Разделение в 3 направлениях. пример
X больше чем P,
меняем его местами с gt, уменьшаем gt.
Слайд 43
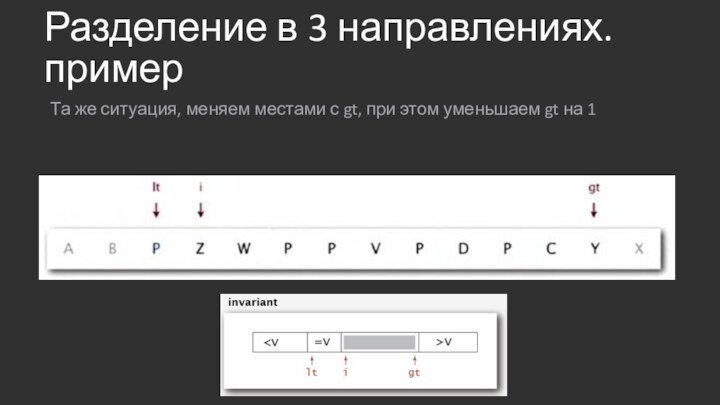
Разделение в 3 направлениях. пример
Та же ситуация, меняем
местами с gt, при этом уменьшаем gt на 1
Слайд 44
Разделение в 3 направлениях. пример
То же самое
Слайд 45
Разделение в 3 направлениях. пример
С < P, уносим
за lt
Слайд 46
Разделение в 3 направлениях. пример
P > W, меняем
местами с gt.
Слайд 47
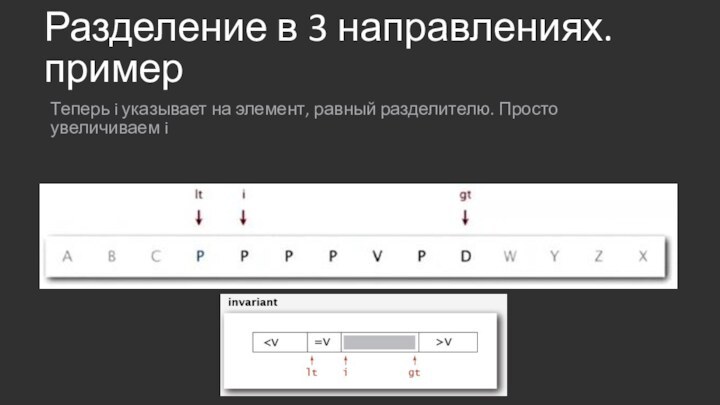
Разделение в 3 направлениях. пример
Теперь i указывает на
элемент, равный разделителю. Просто увеличиваем i
Слайд 48
Разделение в 3 направлениях. пример
Снова P = P,
делаем всё аналогично, пока не получим более-менее отсортированный массив.
Слайд 49
Разделение в 3 направлениях. пример
Слайд 50
Разделение в 3 направлениях. Пошагово
Слайд 51
Разделение в 3 направлениях. реализация
Слайд 52
Повторяющиеся ключи. Нижняя граница
Вывод – Quicksort со случайным
перетасовыванием и разделением в 3 направлениях становится линейным алгоритмом,
а не N*lgN
Слайд 53
ПРОСЫПАЕМСЯ!
Использование разделения в 3 направлениях с Quicksort наиболее
эффективно в случаях кгода входные данные имеют следующее свойство
Все
элементы различны
Есть несколько различных элементов
Элементы расположены в порядке возрастания
Элементы расположены в порядке убывания
Слайд 54
Сортировки в повседневной жизни
Алгоритмы сортировки распространены в огромном
количестве приложений:
Сортировка имен
Библиотеке песен
Выдаче google
RSS-ленте, для сортировки новостей
Поиск медианы
Бинарный
поиск в БД
Поиск повторяющихся email’ов
Сжатие данных
Компьютерная графика
Вычислительная биология
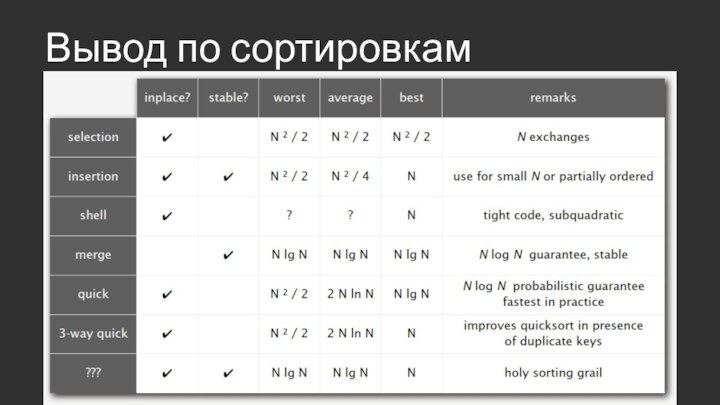
Слайд 55
Какой алгоритм использовать?
Алгоритмов больше, чем мы рассмотрели:
Внутренняя сортировка:
Со
вставкой, с выбором, пузырёк, shaker sort
Quicksort, mergesort, heapsort, samplesort,
сортировка Шелла.
Solitaire sort, red-black sort, splaysort, Yaroslavskiy sort, psort,…
Внешнаяя сортировка. Poly-phase mergesort, cascade-merge, oscillating sort.
Строчные сортировки. Distribution, MSD, LSD, 3-way string quicksort.
Параллельные сортировки.
Bitonic sort, batcher even-odd sort.
Smooth sort, cube sort, column sort.
GPUsort
Слайд 56
Какой алгоритм использовать?
Приложения имеют множество параметров/особенностей
Стабильность
Параллельность
Определенность
Различие ключей
Различие типов
ключей
Массив или ссылочный список
Случайность расположения элементов
И т.д.
Можно использовать одну
сортировку или комбинацию.
НО – учесть все параметры и особенности практически невозможно
Вывод – нет единого «правильного» метода сортировки!




![Быстрая сортировка.quicksort Пример quicksortМы нашли позиции a[i] и a[j], удовлетворяющие условиям относительно a[lo].Меняем a[i] и a[j] местами](/img/tmb/14/1363428/32105fab58857d62fc86f58917685c34-720x.jpg)

![Быстрая сортировка.quicksort Пример quicksortИщем a[i] и a[j], удовлетворяющие условиям.Это a[i] = T и a[j] = I](/img/tmb/14/1363428/591e857ccf7c1be1e05c0c5d64bc05d0-720x.jpg)


![Быстрая сортировка.quicksort Пример quicksortФаза 2 (указатели пересеклись)Меняем местами a[lo] и a[j]Теперь слева от K](/img/tmb/14/1363428/bcdb870d4835262b3fabbe0154876508-720x.jpg)
















![Быстрая сортировка.quicksort Quick-select. Быстрая выборкаРазделяем массив, так что:a[j] находится на местеСлева от j нет](/img/tmb/14/1363428/77ee954307fc5183f97e7a75d2aa06c4-720x.jpg)





![Быстрая сортировка.quicksort Разделение в 3 направлениях. примерПусть v разделитель a[lo]Сканируем i cлева-направо.(a[i] < v):](/img/tmb/14/1363428/8443ecc924b9dcb29ec5a6378f76c2c0-720x.jpg)