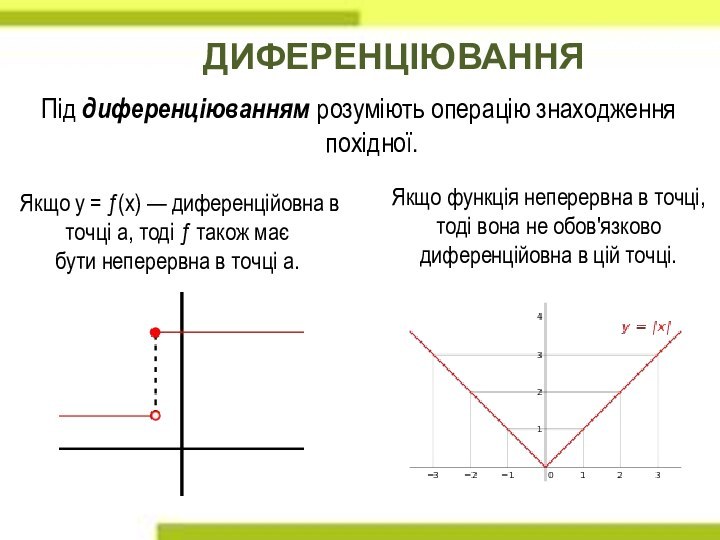
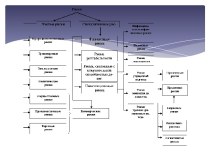
від простих функцій
Похідні від експоненціальних та логарифмічних функцій
Похідні від
тригонометричних функцій:прямих;
обернених.
Похідні від гіперболічних функцій:
прямих;
обернених;
Арифметичні діії над похідними
Використані джерела
Зміст






![Державний вищий навчальний закладЗапорізький національний університетМіністерства освіти та науки України Нехай функція шляхуматеріальної точки, що рухається прямолінійно, залежно від часу t ∈[0;T]](/img/tmb/14/1337467/a86b73f2e70c00e446cec28b1ca54d35-720x.jpg)