Слайд 2
Химический потенциал.
В открытых
системах изменение внутренней энергии ∆U происходит не только в
результате получения или отдачи теплоты и совершения работы, но и за счёт изменения масс, входящих в систему компонентов. Все свойства открытых систем и ΔG будут зависеть от количества каждого компонента:
∆G=µ∆n
,где ΔG энергия Гиббса, µ – химический потенциал, ∆n – изменённое количество вещества системы выраженное в молях.
Химический потенциал – интенсивный параметр состояния. В условиях P,T=const, и сохранения количеств всех других компонентов, μ равен частной производной энергии Гиббса по количеству компонента:
μi = (∂G/∂ni)P,T, i ≠j
Слайд 3
Если из фазы 1 в
фазу 2 переходит вещества, то изменение энергии Гиббса в
фазе 1 будет равно: ΔG1 = -μ1Δn, а в фазе 2: ΔG2 = μ2Δn (знак минус указывает на убыль энергии, плюс на ее увеличение). Общее изменение энергии системы будет равно их сумме
ΔG = -μ1Δn + μ2Δn
Независимо от числа компонентов открытой системы возможен переход любого из них в другую фазу окружающей среды и, наоборот, при условии выравнивания химических потенциалов этого компонента в фазах системы и среды. При равенстве химических потенциалов наступает равновесие между фазами – сколько вещества уходит из системы, столько же и возвращается.
Слайд 4
Диаграммы состояния.
Системы принято классифицировать по
числу компонентов (одно- двухкомпонентные и т.д.), по числу фаз
(одно-, двухфазные и т.д.) и числу степеней свободы (инвариантные, моно-дивариантные и т.д.). Для систем с фазовыми переходами обычно рассматривают графическую зависимость состояния системы от внешних условий – т.н. диаграммы состояния.
Слайд 5
Число степеней свободы (правило фаз Гиббса).
Число степеней свободы гетерогенной термодинамической системы, находящейся в
состоянии фазового равновесия, определяется правилом фаз, сформулированным Дж. Гиббсом:
Число степеней свободы равновесной термодинамической системы С равно числу независимых компонентов системы К минус число фаз Ф плюс число внешних факторов, влияющих на равновесие.
Для системы, на которую из внешних факторов влияют только температура и давление, можно записать:
С = К – Ф + 2
Правило справедливо при следующих предположениях:
1) Фазы имеют достаточно большие размеры, так что поверхностными явлениями можно пренебречь;
2) Каждый компонент может проходить через поверхности раздела фаз (полупроницаемые перегородки отсутствуют).
Слайд 6
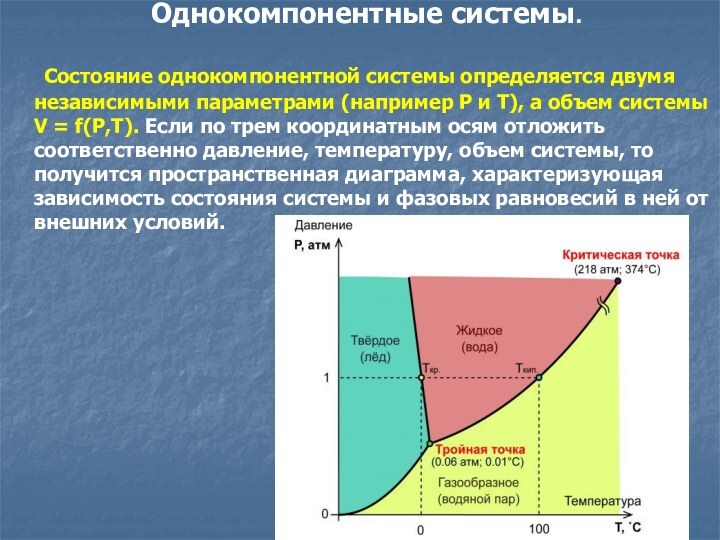
Однокомпонентные системы.
Состояние однокомпонентной системы определяется
двумя независимыми параметрами (например P и T), а объем
системы V = f(P,T). Если по трем координатным осям отложить соответственно давление, температуру, объем системы, то получится пространственная диаграмма, характеризующая зависимость состояния системы и фазовых равновесий в ней от внешних условий.
Слайд 7
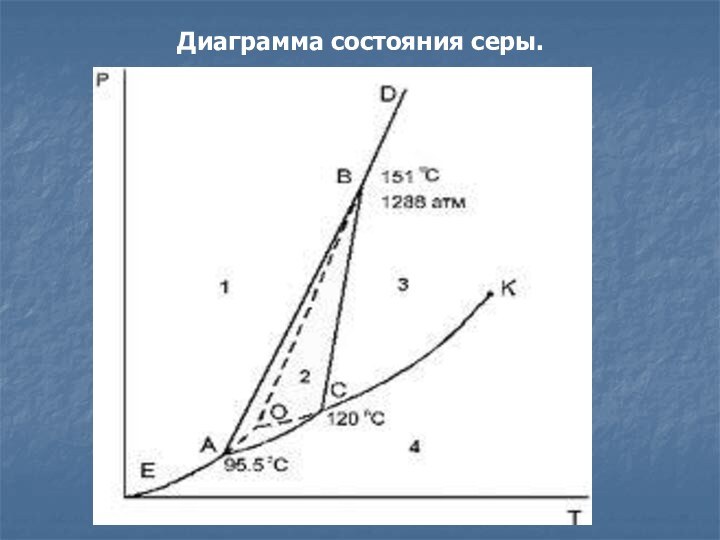
Диаграмма состояния воды при высоких давлениях и низких
температурах.
Слайд 9
Диаграммы состояния двухкомпонентных систем. Термический анализ.
Двухкомпонентными
называются физико-химические системы, в состав которых входят два компонента.
Компонентами могут быть как простые вещества, так и химические соединения. Соотношение между компонентами способно существенно изменять свойства системы. Чтобы определить состояние системы однозначно необходимо знать параметры: Р,Т и концентрации компонентов С1 и С2. Уравнение состояния двухкомпонентной системы имеет вид: f(P,T,C1,C2)=0
Для построения диаграмм состояния используется метод термического анализа.
Слайд 10
Термический анализ.
Метод термического анализа построен на
анализе кривых охлаждения смесей различного состава. Кривая охлаждения это
температурно-временная зависимость охлаждения смеси, показывающая точки фазовых переходов. На рис. приведена форма линий охлаждения (левая часть рис.) на которых, плато соответствует кристаллизации чистого компонента (кр. А и В), точка перегиба – начало кристаллизации одного из компонентов раствора.
Слайд 11
Диаграммы состояния двухкомпонентных систем при полной растворимости веществ
в твердой фазе.
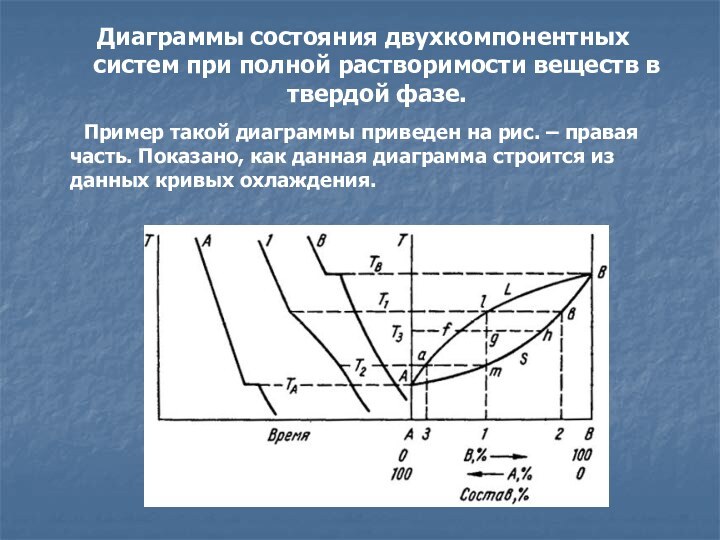
Пример такой диаграммы
приведен на рис. – правая часть. Показано, как данная диаграмма строится из данных кривых охлаждения.
Диаграмма состояния Ag-Au.
Ag и Аu образуют между собой
непрерывный ряд твердых растворов.
Построенные экспериментально кривые
ликвидуса (на фазовых диаграммах
линия полного плавления
твёрдых фаз) и солидуса (линия
на фазовых диаграммах, на
которой исчезают последние
капли расплава, или
температура, при которой
плавится самый легкоплавкий
компонент).
Слайд 13
Диаграммы состояния двухкомпонентных систем без образования области твердых
расторов.
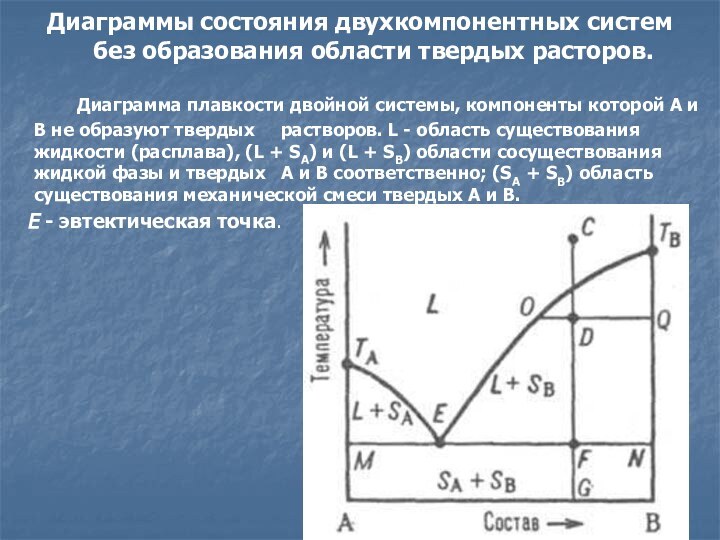
Диаграмма плавкости двойной системы, компоненты
которой А и В не образуют твердых растворов. L - область существования жидкости (расплава), (L + SA) и (L + SB) области сосуществования жидкой фазы и твердых А и В соответственно; (SA + SB) область существования механической смеси твердых А и В.
E - эвтектическая точка.
Слайд 14
На диаграмме состояния линия, изображающая зависимость от
состава температуры начала выделения из жидкой фазы твердого компонента
(начала равновесной кристаллизации), называется линией ликвидуса. Она состоит из двух ветвей ТАЕ и ТВЕ, отграничивающих фазовое поле жидкости L от полей сосуществования жидкой фазы с твердыми А и В соответственно (поля L + SA и L + SB). Линия, изображающая зависимость от состава температуры окончания равновесной кристаллизации при охлаждении (или начала плавления при нагревании), называется линией солидуса. Прямые, соединяющие фигуративные точки двух находящихся в равновесии фаз, называются нодами (или коннодами);
Слайд 15
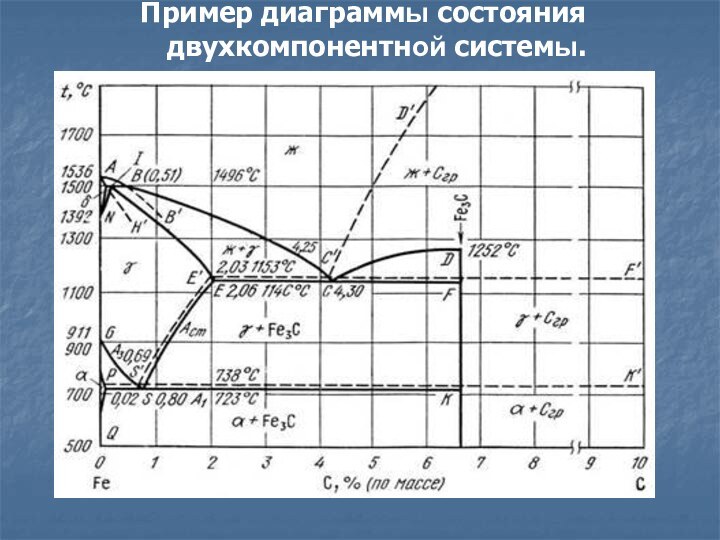
Пример диаграммы состояния двухкомпонентной системы.
Слайд 16
Конденсированное состояние вещества.
Конденсированное состояние
- понятие, объединяющее твёрдые тела и жидкости в противопоставлении
их газу. Атомные частицы (атомы, молекулы, ионы) в конденсированном теле связаны между собой. Ср. энергии теплового движения частиц не хватает на самопроизвольный разрыв связи, поэтому конденсированное тело сохраняет свой объём. Мерой связи атомных частиц служит теплота испарения (в жидкости) и теплота возгонки (в твёрдом теле).
В отличие от газообразного состояния, у вещества в конденсированном состоянии существует упорядоченность в расположении частиц (ионов, атомов, молекул). Кристаллические твёрдые тела обладают высокой степенью упорядоченности - дальним порядком в расположении частиц.
Слайд 17
Аморфные соединения.
Аморфные соединения помимо высокоэластического
могут находиться в двух других физ. состояниях: стеклообразном состоянии
и вязко-текучем состоянии. высокомолекулярные соединения, которые переходят из высоко-эластичных состояния в стеклообразное при температурах ниже комнатной, относят к эластомерам, при более высокой температуре к пластикам. Кристаллические высокомолекулярные соединения обычно являются пластиками.
Слайд 18
Кристаллы и их виды.
Кристаллы — это твёрдые
вещества, имеющие естественную внешнюю форму правильных симметричных многогранников, основанную
на их внутренней структуре, то есть на одном из нескольких определённых регулярных расположений составляющих вещество частиц (атомов, молекул, ионов).
Идеальный кристалл
Является, по сути, математическим объектом, имеющим полную, свойственную ему симметрию, идеализированно ровные гладкие грани и т. д.
Реальный кристалл
Всегда содержит различные дефекты внутренней структуры решетки, искажения и неровности на гранях и имеет пониженную симметрию многогранника вследствие специфики условий роста, неоднородности питающей среды, повреждений и деформаций.
Основной отличительный признак кристаллов — присущее им свойство анизотропии, то есть зависимость их свойств от направления, тогда как в изотропных (жидкостях, аморфных твёрдых телах) или псевдоизотропных (поликристаллы) телах свойства от направлений не зависят.
Слайд 19
Свойства кристаллов в зависимости от вида химических связей.
Типы химической связи — это удобное
упрощение. Более точно поведение электрона в кристалле описывается законами квантовой механики. Говоря о типе связи в кристалле, необходимо иметь в виду следующее:
Связь между двумя атомами никогда полностью не соответствует одному из описанных типов. В ионной связи всегда присутствует элемент ковалентной связи и т.п.
В сложных веществах связь между разными атомами может быть разного типа. Так например, в кристалле белка связь в молекуле белка ковалентная, а между молекулами (или разными частями одной молекулы) водородная.
Слайд 20
Ковалентная связь
Ковалентная связь (атомная
связь) — химическая связь, образованная перекрытием (обобществлением) пары валентных электронных
облаков. Обеспечивающие связь электронные облака (электроны) называются общей электронной парой
Кристаллы с ковалентной связью диэлектрики или полупроводники. Типичными примерами атомных кристаллов могут служить алмаз, германий и кремний
Слайд 21
Ионная связь.
Ионная связь — очень
прочная химическая связь, образующаяся между атомами с большой разностью электроотрицательностей,
при которой общая электронная пара полностью переходит к атому с большей электроотрицательностью. Силы взаимодействия между узлами являются в основном электростатическими (кулоновскими). Связь между такими частицами называется гетерополярной или ионной.
Слайд 22
Металлическая связь.
Металлическая связь — это одновременное существование
положительно заряженных атомов и свободного электронного газа.Во всех узлах
кристаллической решётки расположены положительные ионы металла. Между ними беспорядочно, подобно молекулам газа, движутся валентные электроны, отщепившиеся от атомов при образовании ионов. Вместе с тем и электроны удерживаются ионами в пределах кристаллической решётки и не могут её покинуть. Свободно движущиеся электроны обусловливают высокую электро- и теплопроводность.
Слайд 23
Молекулярная связь.
В узлах кристаллической решётки помещаются
определённым образом ориентированные молекулы. Силы связи между молекулами в
кристалле имеют ту же природу, что и силы притяжения между молекулами, приводящие к отклонению газов от идеальности. По этой причине их называют ван-дер-ваальсовскими силами.
Для кристаллов с молекулярными связями характерны низкие температуры плавления и высокая сжимаемость.
Молекулярные связи образуют, например, следующие вещества : H2, N2, O2, CO2, H2O.