Слайд 2
Часто при работе с таблицами возникает необходимость применить
одну и ту же операцию к целому диапазону ячеек
или произвести расчеты по формулам, зависящим от большого массива данных.
Под массивом в MS Excel понимается прямоугольный диапазон формул или значений, которые программа обрабатывает как единую группу.
Слайд 3
1. Умножение элементов массива на число
В качестве примера
использования формулы массива приведем расчет цен группы товаров с
учетом НДС (налог на добавленную стоимость).
Пусть в диапазоне В2:В4 даны цены группы товаров без учета НДС. Необходимо найти цену каждого товара с учетом НДС, который будем полагать равным 25%.
Слайд 4
Таким образом, необходимо умножить массив элементов В2:В4 на
125%. Результат надо разместить в ячейках диапазона С2:С4. Для
этого:
следует выделить диапазон С2:С4, ввести формулу
=В2:В4*125%
завершить ввод формулы не нажатием клавиши , а нажатием комбинации клавиш ++.
Таким образом, вы сообщите MS Excel, что необходимо выполнить операцию над массивом, т.е. создать формулу массива.
В ответ MS Excel автоматически возьмет формулу в фигурные скобки:
{=B2:B4*125%}
Слайд 5
Умножение элементов массива на число
Слайд 6
2. Поэлементное сложение, вычитание,
умножение и деление двух массивов
Рассмотрим
операцию поэлементного сложения двух массивов.
Пусть, например, слагаемыми будут
массивы, содержащиеся в диапазонах А2:В3 и D2:E3.
Слайд 7
Необходимо выделить на рабочем листе диапазон, например, G2:H3,
в который будет помещен результат поэлементного сложения двух массивов.
От данного диапазона требуется, чтобы он имел тот же размер, что и массивы-слагаемые.
Далее следует ввести формулу
=А2:В3+D2:E3
Слайд 8
Завершить ввод следует нажатием комбинации клавиш
++.
MS
Excel возьмет формулу в строке формул в фигурные скобки
и произведет требуемые вычисления:
{=А2:В3+D2:E3}
Слайд 9
Аналогично можно вычислить поэлементно разность, произведение и деление
массивов.
Для избежания ошибок в формулу вводите ссылки на диапазоны
ячеек не с клавиатуры, а путем выбора их на рабочем листе мышью. Тогда ссылка на диапазон ячеек в формулу будет вводиться автоматически.
Слайд 10
3. Вычисление сложных выражений
Приведем более сложный пример использования
формул массива, а именно: попытаемся найти значение следующего выражения:
где
Х – вектор из n компонентов, В и С – матрицы размера m x m, причем, n = 3, m = 2
Слайд 11
Для вычисления значения S необходимо:
ввести в
диапазон А2:А4 компоненты вектора Х;
ввести в диапазон В2:С3 компоненты
матрицы В;
ввести в диапазон D2:E3 компоненты матрицы С.
Слайд 12
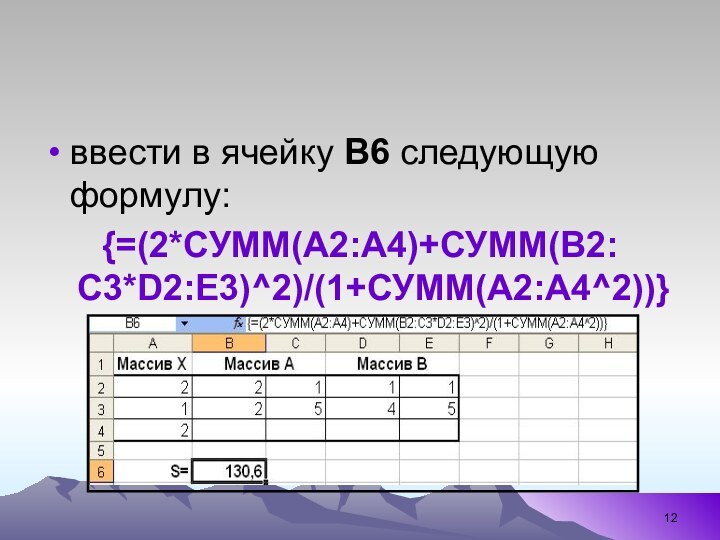
ввести в ячейку В6 следующую формулу:
{=(2*СУММ(А2:А4)+СУММ(В2:С3*D2:E3)^2)/(1+СУММ(А2:А4^2))}
Слайд 13
4. Функции
для работы с матрицами
В MS Excel имеются
функции для работы с матрицами, перечисленные в таблице:
Слайд 14
Пример 1. Решение системы линейных уравнений
Решение
линейной системы уравнений АХ = В, где
А –
матрица коэффициентов,
В – столбец (вектор) свободных членов,
Х – столбец (вектор) неизвестных,
имеет вид Х = А-1В, где А-1 – обратная матрица к А.
Слайд 15
Пусть:
Введем исходные данные задачи на рабочий лист EXCEL:
Слайд 16
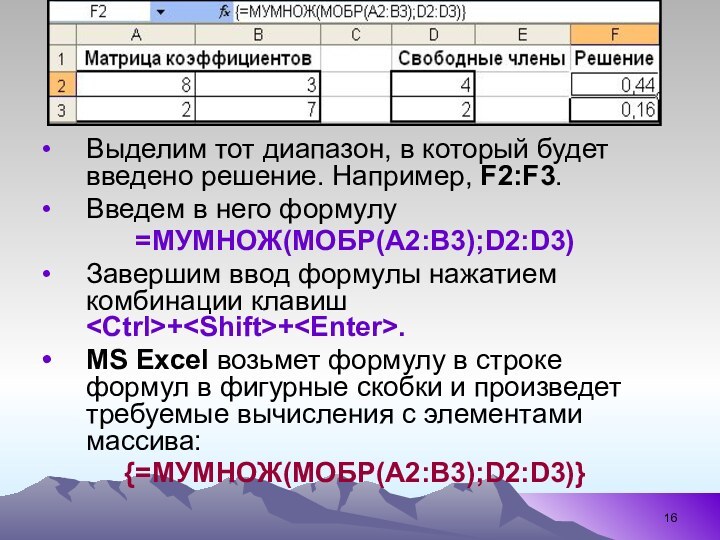
Выделим тот диапазон, в который будет введено решение.
Например, F2:F3.
Введем в него формулу
=МУМНОЖ(МОБР(А2:В3);D2:D3)
Завершим ввод формулы нажатием комбинации
клавиш ++.
MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива:
{=МУМНОЖ(МОБР(А2:В3);D2:D3)}
Слайд 17
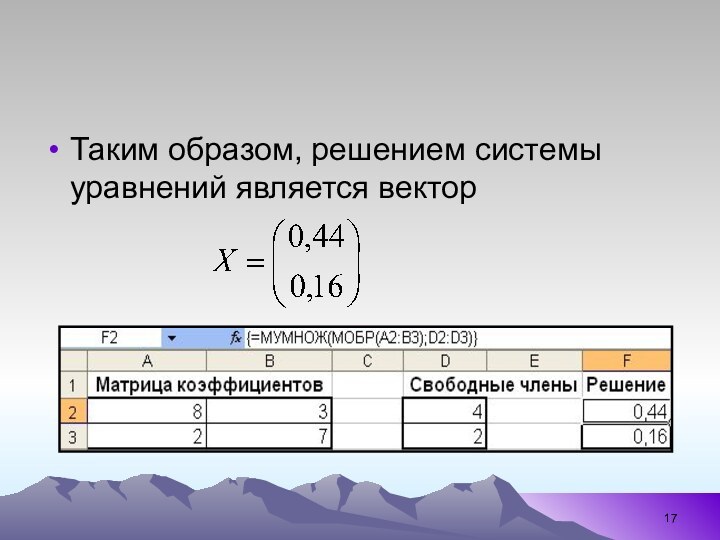
Таким образом, решением системы уравнений является вектор
Слайд 18
Пример 2. Решение системы линейных уравнений
В качестве более
сложного примера решим систему линейных уравнений
А2Х = В,
где
Решением этой системы является вектор Х = (А2)-1В.
Слайд 19
Для нахождения вектора Х:
Введем элементы матрицы
А и вектора B.
Выберем диапазон F2:F3, куда поместим
элементы вектора решения.
Введем в этот диапазон формулу:
Слайд 20
=МУМНОЖ(МОБР(МУМНОЖ(А2:В3; А2:В3));D2:D3)
Завершим ввод формулы нажатием комбинации клавиш ++.
MS Excel возьмет формулу в строке формул в фигурные
скобки и произведет требуемые вычисления с элементами массива:
{=МУМНОЖ(МОБР(МУМНОЖ(А2:В3; А2:В3));D2:D3)}
Слайд 21
В диапазоне ячеек F2:F3 будет найдено решение системы
уравнений:
Слайд 22
5. Нахождение значения
квадратичной формы
Рассмотрим пример вычисления квадратичной
формы ,
при этом
Для нахождения этой квадратичной формы:
Введем элементы матрицы A и вектора X.
Слайд 23
Выберем ячейку F2 для вычисления значения формы.
Введем формулу:
=МУМНОЖ(МУМНОЖ(ТРАНСП(D2:D3);
A2:B3);D2:D3)
Завершим ввод формулы нажатием комбинации клавиш ++. MS Excel
возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива:
{=МУМНОЖ(МУМНОЖ(ТРАНСП(D2:D3); A2:B3);D2:D3)}
Слайд 24
В ячейке F2 будет получено искомое значение формы
196.
Слайд 25
Примеры использования матричных операций в экономических задачах
Пример 1.
Данные о доходах (тыс. ден. ед.) холдинга по трем
регионам трех компаний за 2008 и 2009 гг. представлены в матрицах А и В:
Слайд 26
Здесь элемент aij матрицы А означает доход i-й
компании в j-м регионе за 2008 г. Аналогично –
для матрицы В, но за 2009 г.
Вычислить матрицу С приростов доходов за период с 2008 по 2010 г. и проанализировать ее.
Рассчитать матрицу Сср, характеризующую средние размеры приростов доходов компаний холдинга за год.
Слайд 27
Решение.
1) Матрица С приростов доходов за рассматриваемый период
равна: С = В –
А.
Элементы матрицы С выражают изменение доходов с 2008 по 2010 г. Так, третья компания по первому региону потерпела убытки в размере 40 тыс. ден. ед. (c31 = - 40), эта же компания (третья) по третьему региону в этот же период не принесла доходов (с33 = 0).
Слайд 28
2) Матрица Сср, характеризующая средние размеры приростов доходов
компаний холдинга за год, равна матрице С, деленной на
n – количество лет в рассматриваемом периоде. В период с 2008 по 2010 г. входит 2 года (т.е. 2008 и 2009гг.), значит, n = 2, тогда: Сср = C/2.
Слайд 29
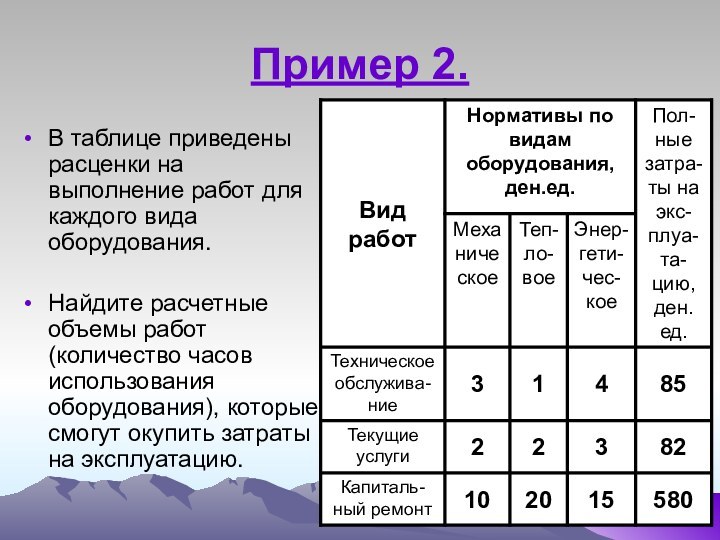
Пример 2.
В таблице приведены расценки на выполнение работ
для каждого вида оборудования.
Найдите расчетные объемы работ (количество часов
использования оборудования), которые смогут окупить затраты на эксплуатацию.
Слайд 30
Решение.
Пусть необходимо х1 ч работы механического оборудования, х2
ч работы теплового оборудования и х3 ч работы энергетического
оборудования, чтобы окупить затраты на техническое обслуживание, текущие услуги и капитальный ремонт.
Тогда из условий задачи следует система уравнений:
3х1 + х2 + 4х3 = 85
2х1 + 2х2 + 3х3 = 82
10х1 +20х2 + 15х3 = 580
Слайд 31
или в матричной форме АХ = В,
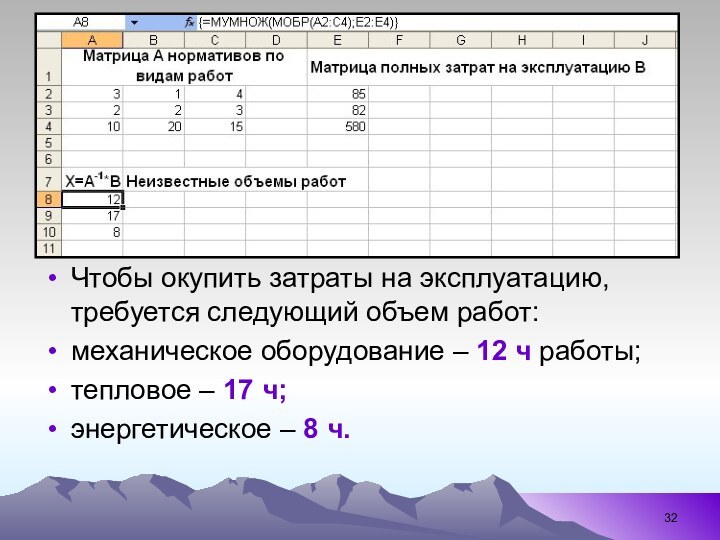
где