Слайд 2
Периодическим называется повторяющееся движение, у которого каждый цикл
в точности воспроизводит любой другой цикл.
Продолжительность одного цикла называется
периодом.
Период равномерного вращения равен продолжительности одного оборота.
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени.
В зависимости от природы повторяющегося процесса различают колебания:
Механические,
Электромагнитные,
Электромеханические и др.
Слайд 3
В зависимости от характера воздействия на колеблющуюся систему
различают:
Свободные (собственные) колебания,
Вынужденные колебания,
Автоколебания,
Параметрические колебания.
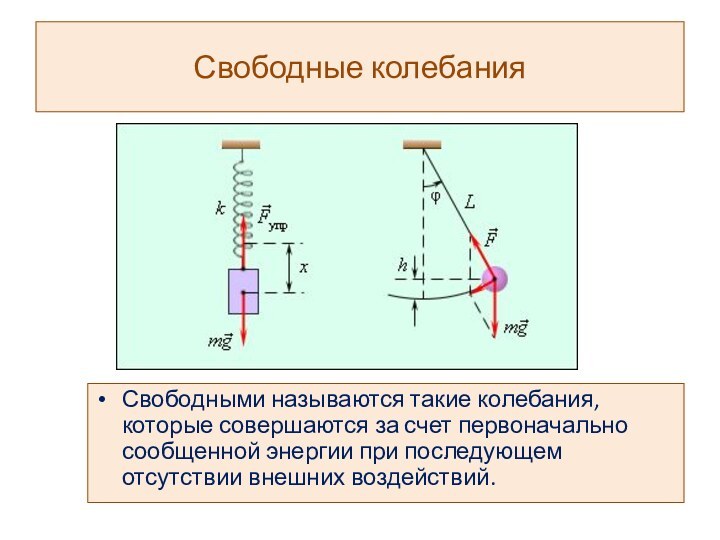
Свободными называются такие колебания, которые
совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий.
Слайд 4
Свободные колебания
Свободными называются такие колебания, которые совершаются за
счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий.
Слайд 5
Вынужденные колебания
Вынужденными называются такие колебания, в процессе которых
колеблющаяся система подвергается воздействию внешней периодической изменяющейся силы.
Слайд 6
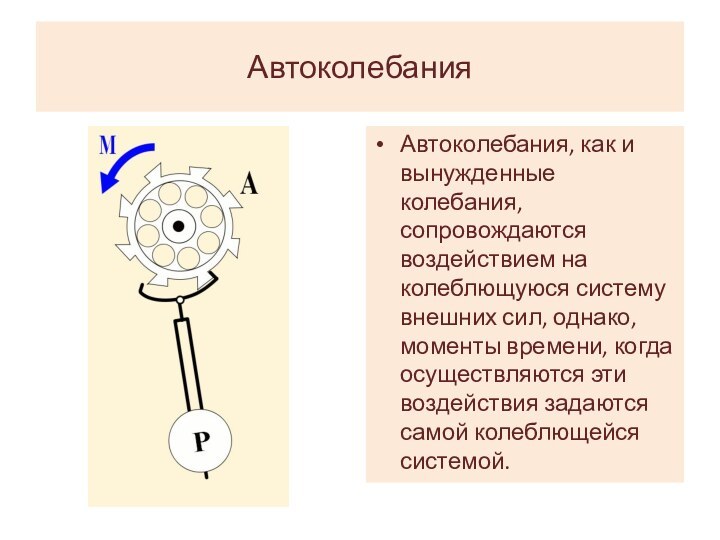
Автоколебания
Автоколебания, как и вынужденные колебания, сопровождаются воздействием на
колеблющуюся систему внешних сил, однако, моменты времени, когда осуществляются
эти воздействия задаются самой колеблющейся системой.
Слайд 7
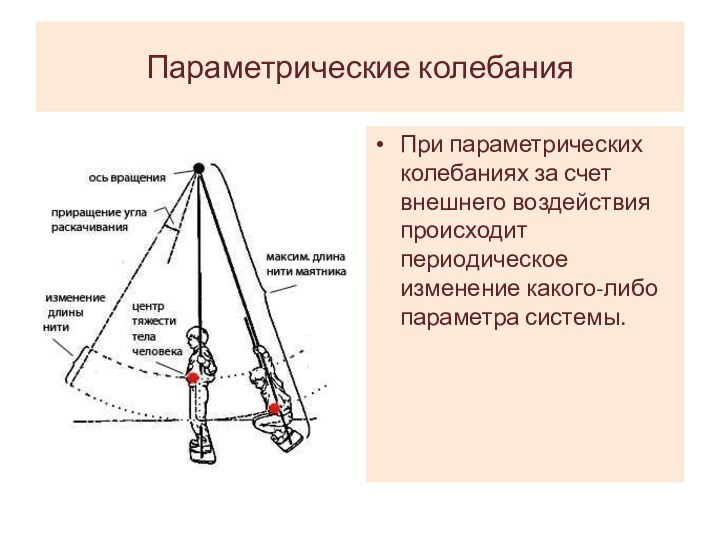
Параметрические колебания
При параметрических колебаниях за счет внешнего воздействия
происходит периодическое изменение какого-либо параметра системы.
Слайд 8
Гармонические колебания
Гармонические колебания – это колебания, при которых
колеблющаяся величина (например, отклонение маятника) изменяется по закону синуса
или косинуса.
Слайд 9
Гармонические колебания
Т=2π – период,
А –амплитуда колебаний (максимальное значение
колеблющейся величины),
ϕ – начальная фаза колебаний (рад),
t – время
колебаний (с),
Х – колеблющаяся величина (удаление от положения равновесия в любой момент времени).
Слайд 10
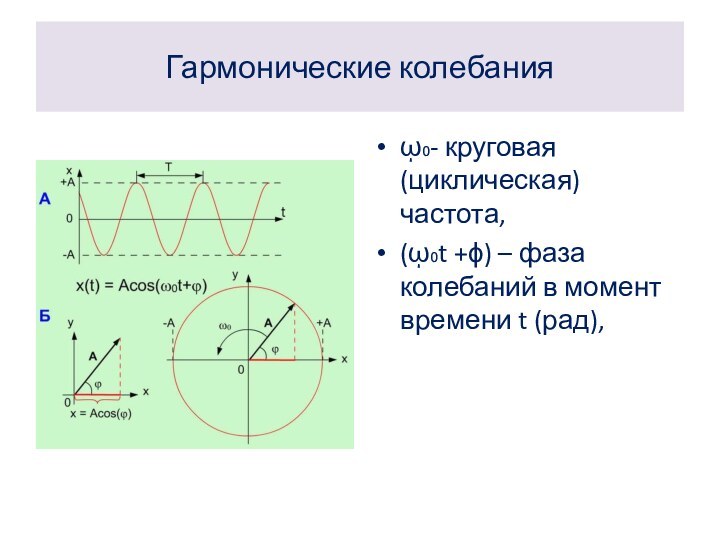
Гармонические колебания
ῳ₀- круговая (циклическая) частота,
(ῳ₀t +ϕ) – фаза
колебаний в момент времени t (рад),
Слайд 11
Гармонические колебания
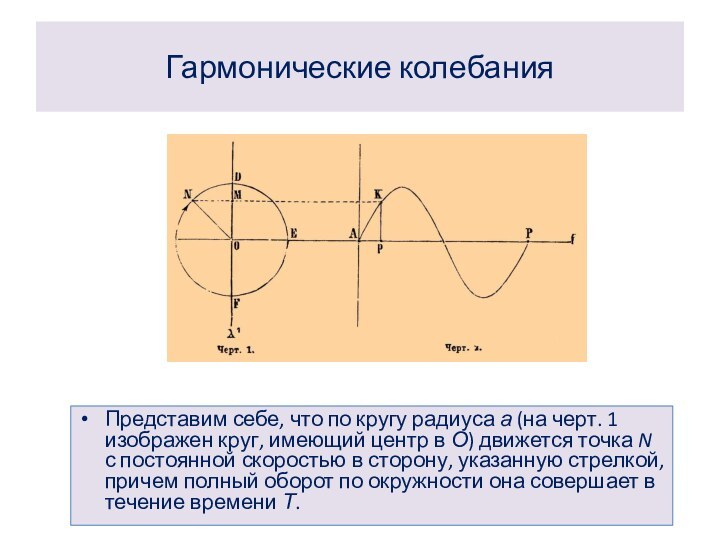
Представим себе, что по кругу радиуса а
(на черт. 1 изображен круг, имеющий центр в О)
движется точка N с постоянной скоростью в сторону, указанную стрелкой, причем полный оборот по окружности она совершает в течение времени Т.
Слайд 13
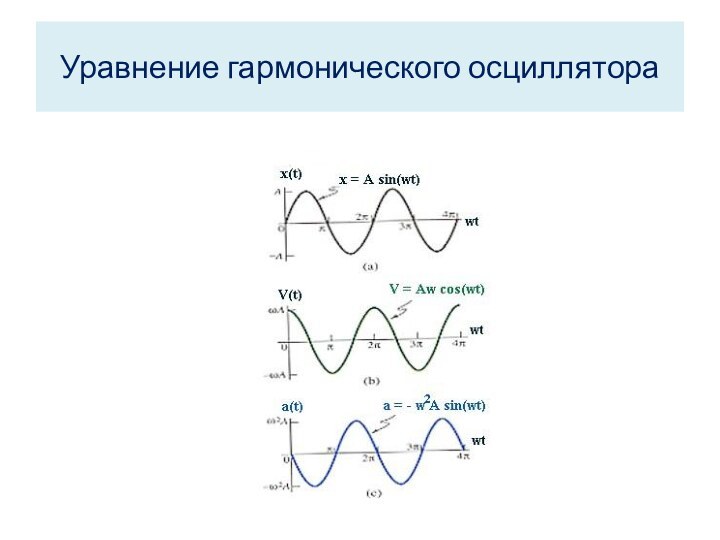
Уравнение гармонического осциллятора
Слайд 14
Уравнение гармонического осциллятора
Слайд 15
Уравнение гармонического осциллятора
Слайд 16
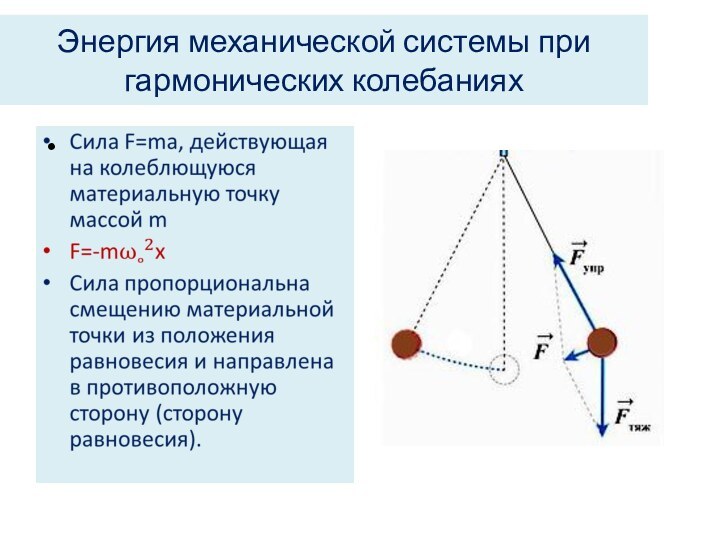
Энергия механической системы при гармонических колебаниях
Слайд 17
Энергия механической системы при гармонических колебаниях
Кинетическая энергия материальной
точки, совершающей прямолинейные гармонические колебания
Слайд 18
Энергия механической системы при гармонических колебаниях
Потенциальная энергия материальной
точки, совершающей гармонические колебания под действием упругой силы F
Слайд 19
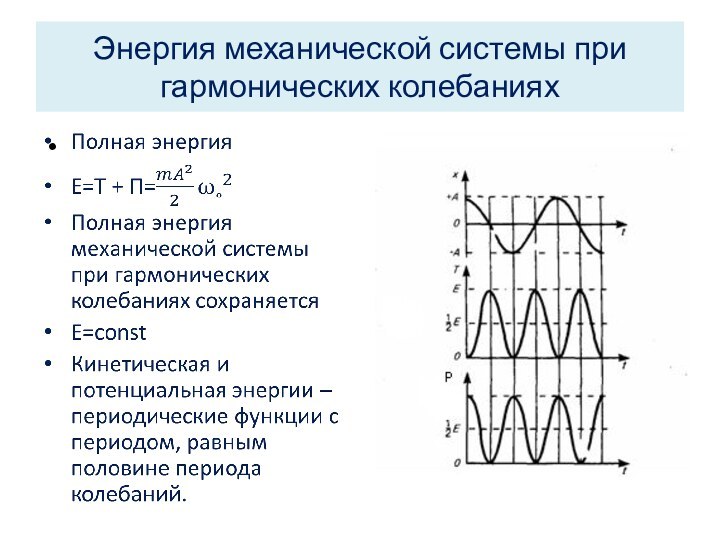
Энергия механической системы при гармонических колебаниях
Слайд 20
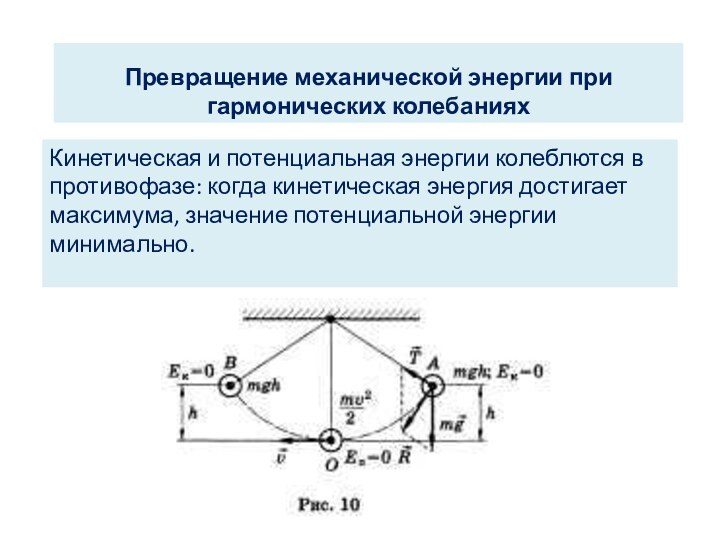
Превращение механической энергии при гармонических колебаниях
Кинетическая и потенциальная
энергии колеблются в противофазе: когда кинетическая энергия достигает максимума,
значение потенциальной энергии минимально.
Слайд 22
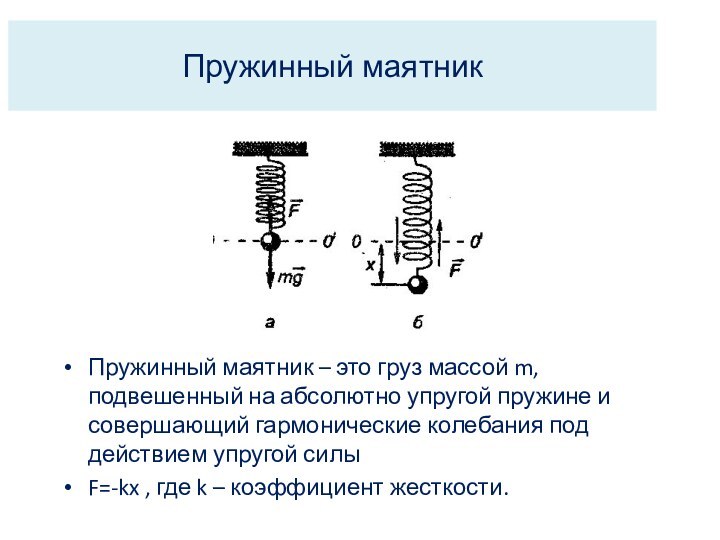
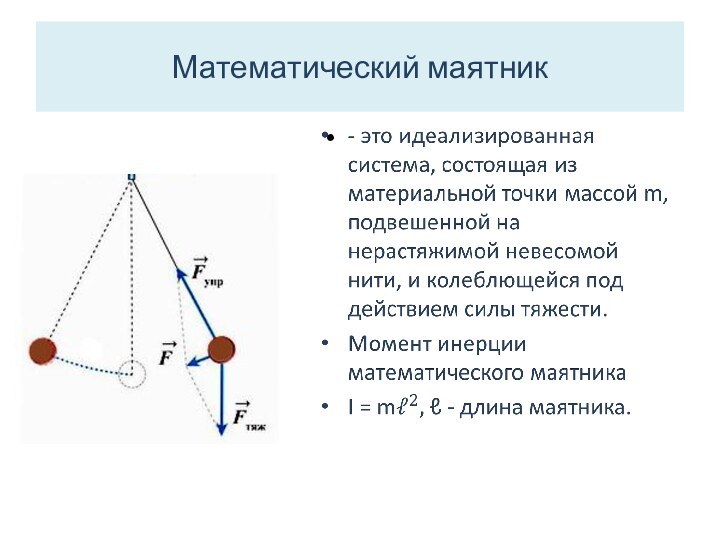
Пружинный маятник
Пружинный маятник – это груз массой m,
подвешенный на абсолютно упругой пружине и совершающий гармонические колебания
под действием упругой силы
F=-kx , где k – коэффициент жесткости.
Слайд 24
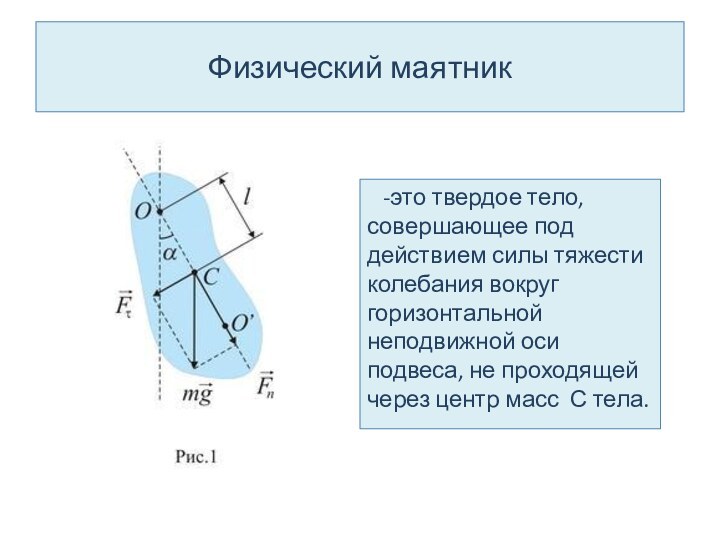
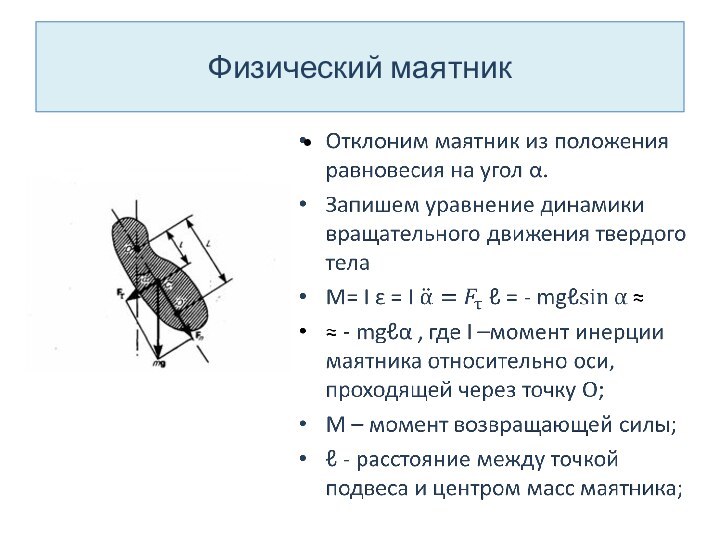
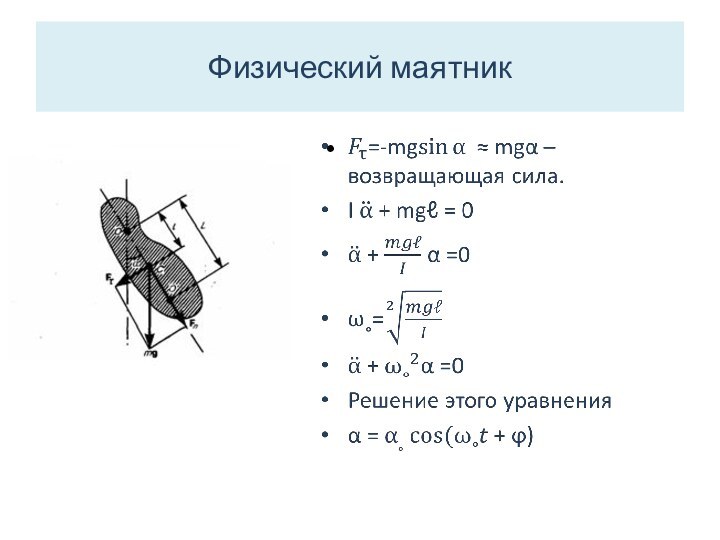
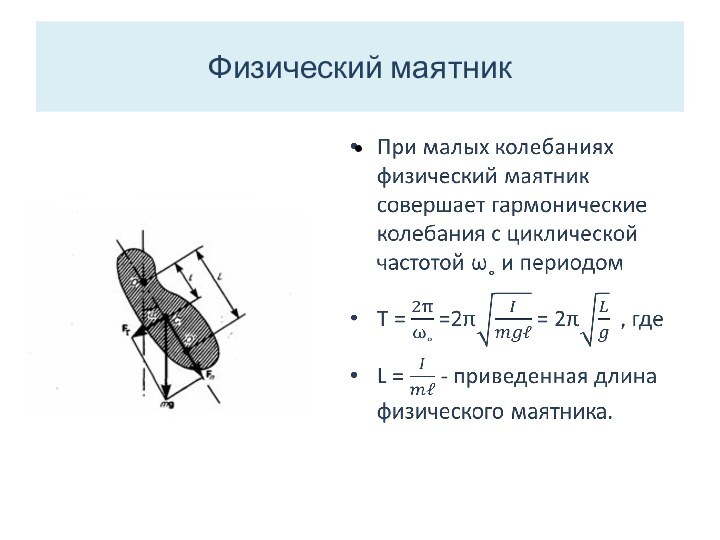
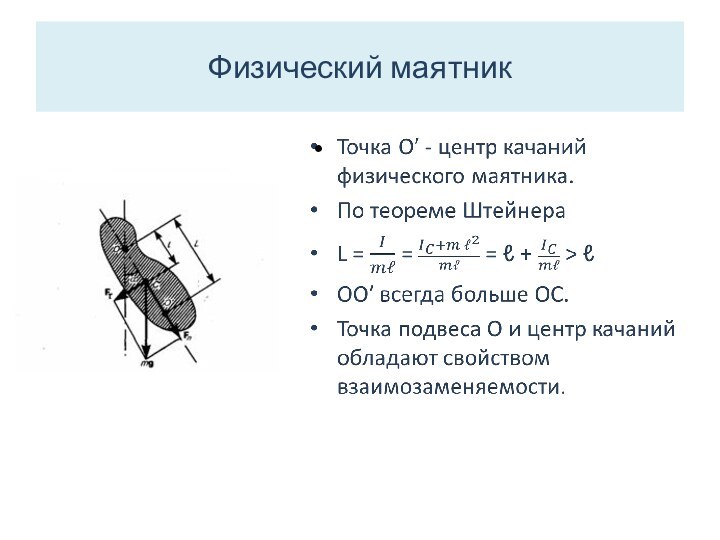
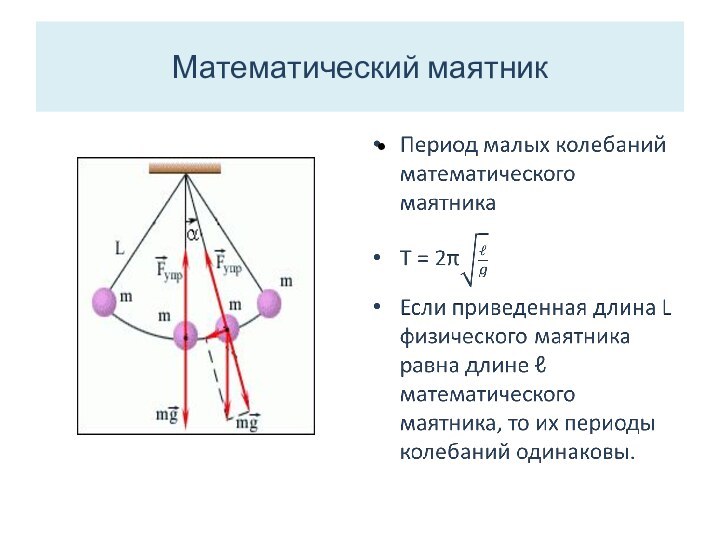
Физический маятник
-это твердое тело, совершающее под
действием силы тяжести колебания вокруг горизонтальной неподвижной оси подвеса,
не проходящей через центр масс С тела.
Слайд 31
Представление гармонических колебаний методом векторных диаграмм
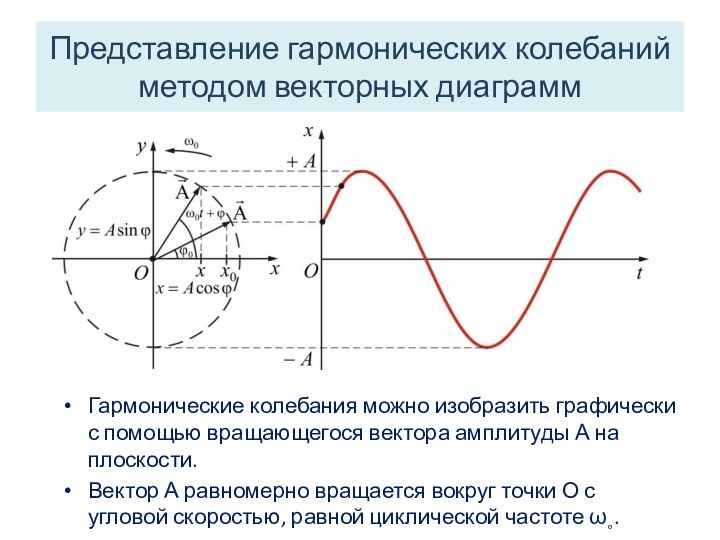
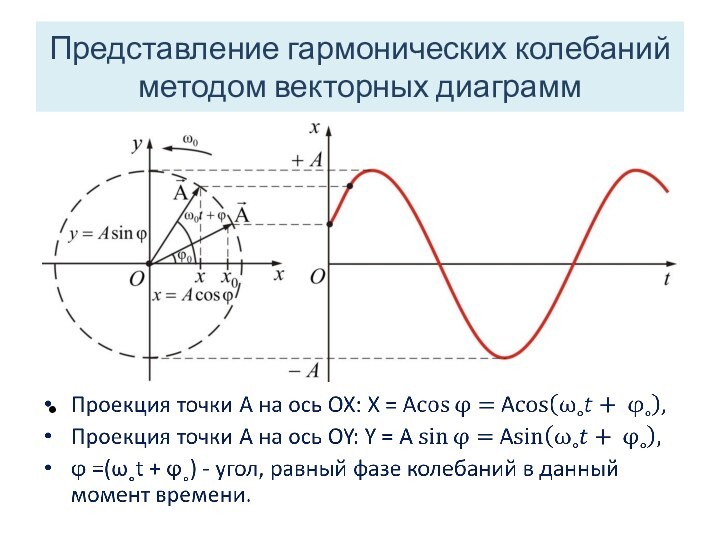
Гармонические колебания можно
изобразить графически с помощью вращающегося вектора амплитуды А на
плоскости.
Вектор А равномерно вращается вокруг точки О с угловой скоростью, равной циклической частоте ω˳.
Слайд 32
Представление гармонических колебаний методом векторных диаграмм
Слайд 33
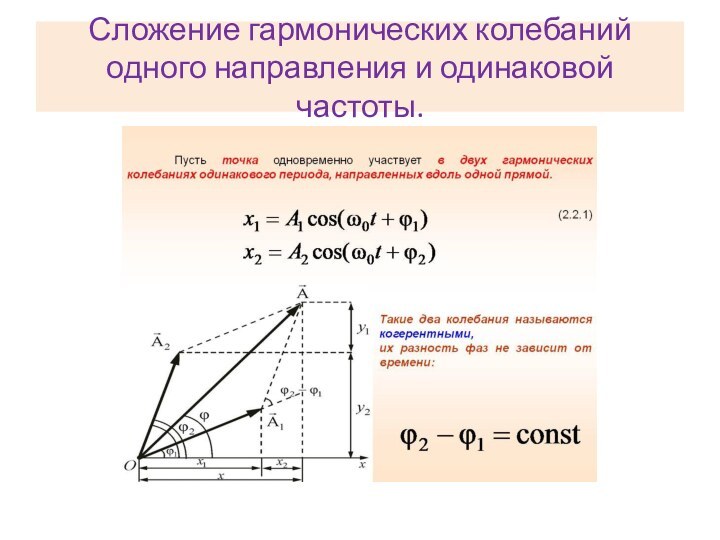
Сложение гармонических колебаний
Под сложением колебаний понимают нахождение закона
результирующих колебаний, когда эта система одновременно участвует в нескольких
колебательных процессах.
Различают два предельных случая: сложение колебаний одинакового направления и сложение взаимно перпендикулярных колебаний.
Например, груз подвешен на пружине к потолку рессорного вагона. Груз будет совершать колебания относительно точки подвеса, которая в свою очередь совершает колебания на рессорах вагона. Т.о. груз будет совершать движение, складывающееся из двух колебаний одного направления.
Слайд 34
Сложение гармонических колебаний одного направления и одинаковой частоты.
Слайд 35
Сложение гармонических колебаний одного направления и одинаковой частоты.
Слайд 36
Сложение гармонических колебаний одного направления и одинаковой частоты.
Слайд 38
Биения
- результирующее колебание при условии Δω/2˂˂ω
- амплитуда биения
частота
биений
период биений
Слайд 39
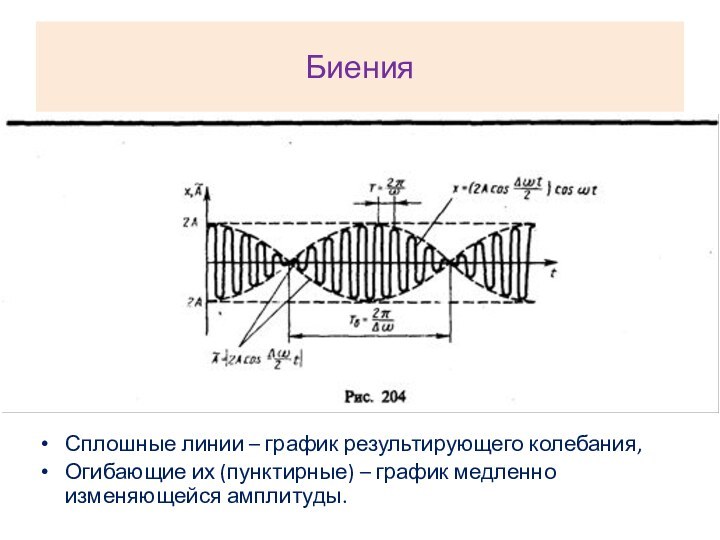
Биения
Сплошные линии – график результирующего колебания,
Огибающие их (пунктирные)
– график медленно изменяющейся амплитуды.
Слайд 40
Сложение взаимно перпендикулярных колебаний
Колебания происходят во взаимно перпендикулярных
направлениях х и у с одинаковой частотой ω ,
начальная фаза первого колебания =0, тогда α – разность фаз колебаний,
А и В – амплитуды складываемых колебаний.
Слайд 41
Сложение взаимно перпендикулярных колебаний
Уравнение результирующего колебания у =
у (х).
Уравнение эллипса.
Такие колебания называются эллиптически поляризованными.
Ориентация осей эллипса
и его размеры зависят от амплитуд складываемых колебаний и разности фаз α.
Слайд 42
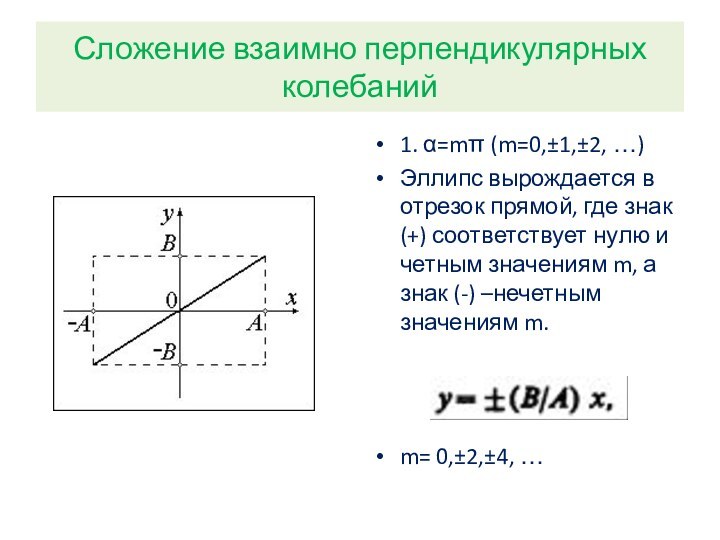
Сложение взаимно перпендикулярных колебаний
1. α=mπ (m=0,±1,±2, …)
Эллипс вырождается
в отрезок прямой, где знак (+) соответствует нулю и
четным значениям m, а знак (-) –нечетным значениям m.
m= 0,±2,±4, …
Слайд 43
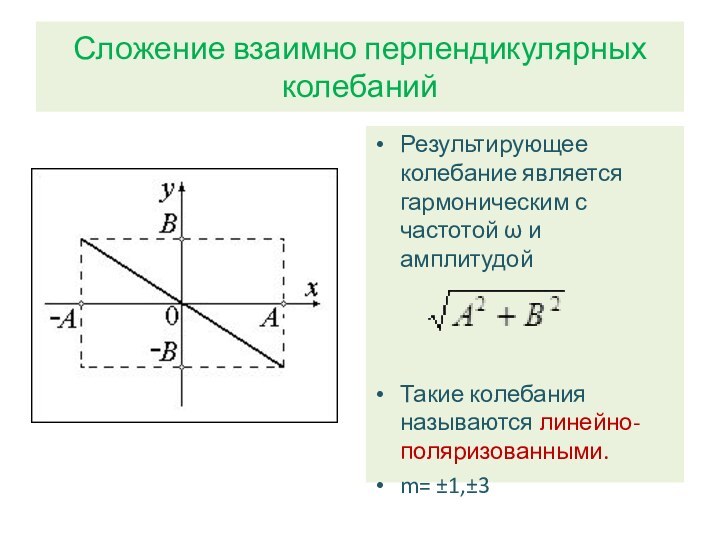
Сложение взаимно перпендикулярных колебаний
Результирующее колебание является гармоническим с
частотой ω и амплитудой
Такие колебания называются линейно-поляризованными.
m= ±1,±3
Слайд 44
Сложение взаимно перпендикулярных колебаний
2. α=(2m+1)π/2 m=0,±1,±2, уравнение
имеет вид эллипса.
Слайд 45
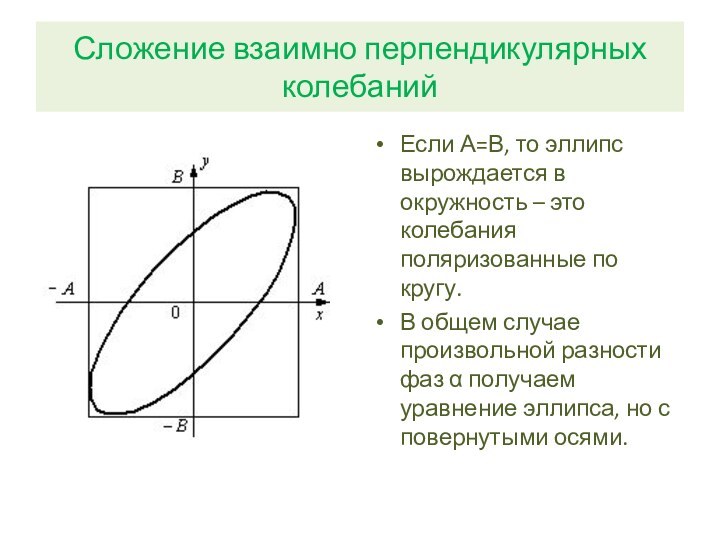
Сложение взаимно перпендикулярных колебаний
Если А=В, то эллипс вырождается
в окружность – это колебания поляризованные по кругу.
В общем
случае произвольной разности фаз α получаем уравнение эллипса, но с повернутыми осями.
Слайд 46
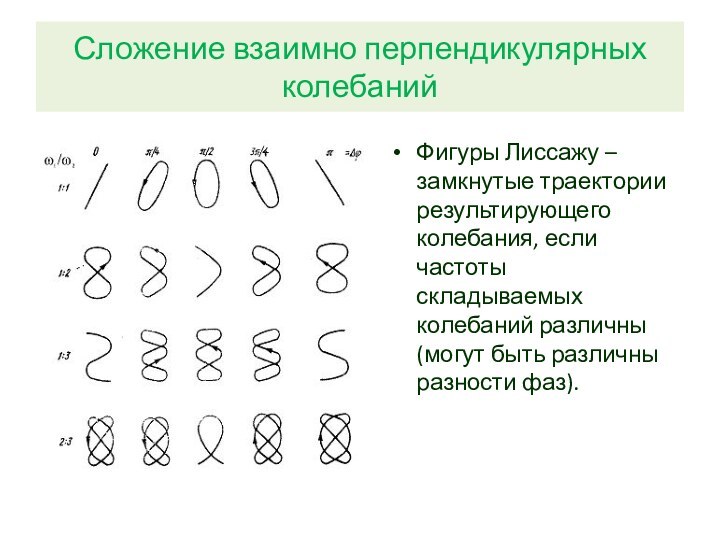
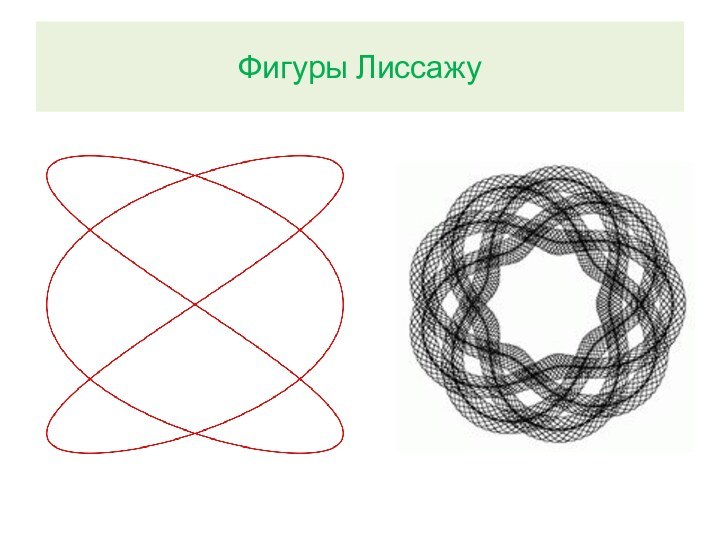
Сложение взаимно перпендикулярных колебаний
Фигуры Лиссажу – замкнутые траектории
результирующего колебания, если частоты складываемых колебаний различны (могут быть
различны разности фаз).
Слайд 48
Дифференциальное уравнение свободных затухающих колебаний
Свободные затухающие колебания- это
колебания амплитуда которых из-за потерь энергии реальной колебательной системой
с течением времени уменьшается.
Простейшим механизмом уменьшения энергии колебаний является превращение ее в теплоту вследствие трения в механических колебательных системах.
Слайд 49
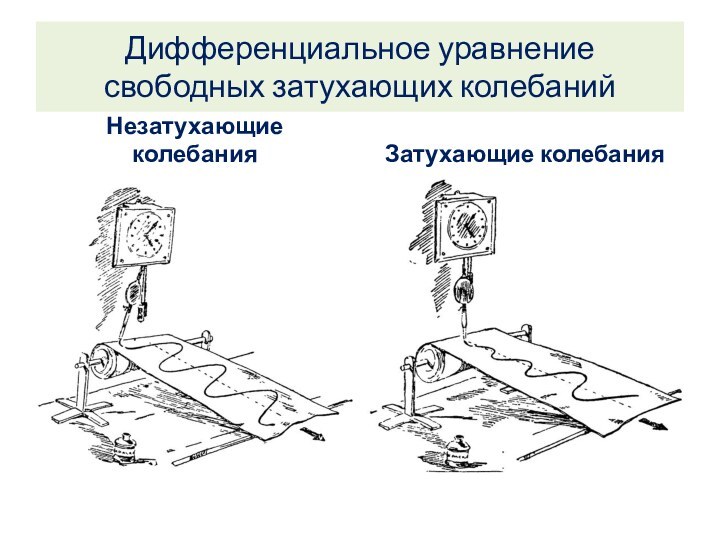
Дифференциальное уравнение свободных затухающих колебаний
Незатухающие колебания
Затухающие колебания
Слайд 50
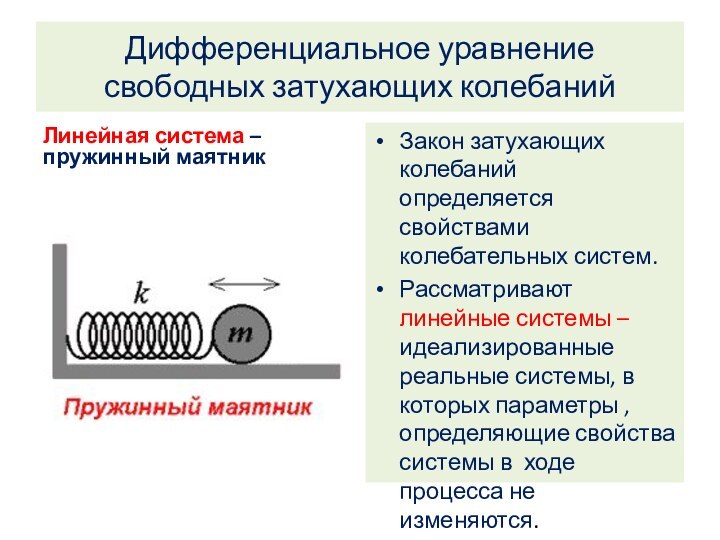
Дифференциальное уравнение свободных затухающих колебаний
Линейная система –пружинный маятник
Закон
затухающих колебаний определяется свойствами колебательных систем.
Рассматривают линейные системы –
идеализированные реальные системы, в которых параметры , определяющие свойства системы в ходе процесса не изменяются.
Слайд 51
Дифференциальное уравнение свободных затухающих колебаний
S – колеблющаяся величина
(переменная) – смещение, заряд и др.
δ = const –
коэффициент затухания,
ω˳- циклическая частота свободных незатухающих колебаний,
δ = 0 – отсутствие потерь энергии.
1
Слайд 52
Дифференциальное уравнение свободных затухающих колебаний
Слайд 53
Дифференциальное уравнение свободных затухающих колебаний
Слайд 54
Дифференциальное уравнение свободных затухающих колебаний
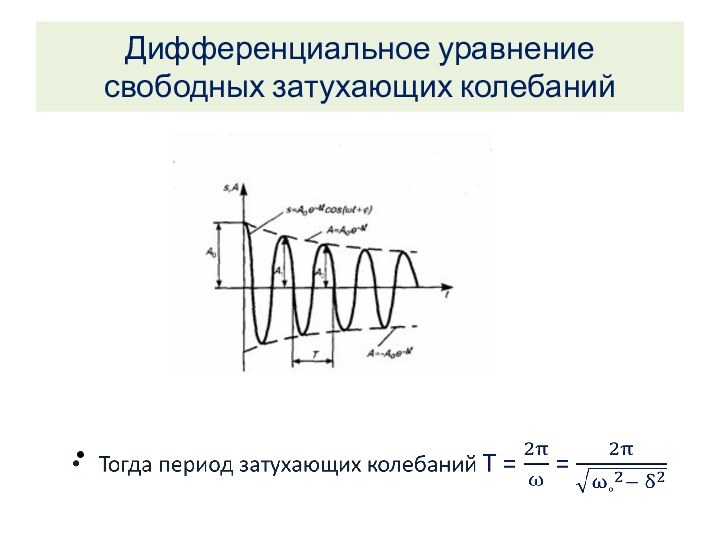
Затухание нарушает периодичность колебаний,
поэтому затухающие колебания не являются периодическими и к ним
нельзя применять понятие периода или частоты.
Однако, если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами.
Слайд 55
Дифференциальное уравнение свободных затухающих колебаний
Слайд 56
Дифференциальное уравнение свободных затухающих колебаний
Слайд 57
Дифференциальное уравнение свободных затухающих колебаний
3
Слайд 58
Дифференциальное уравнение свободных затухающих колебаний
Слайд 59
Свободные затухающие колебания пружинного маятника
Слайд 60
Свободные затухающие колебания пружинного маятника
Слайд 62
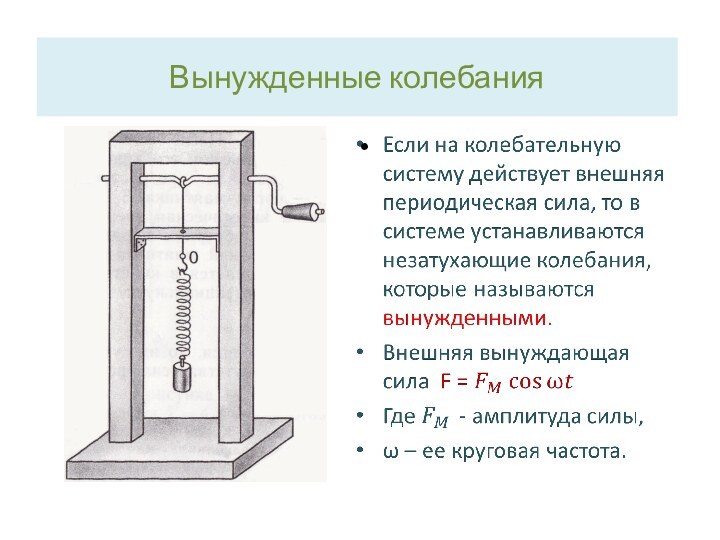
Вынужденные колебания
Опыт показывает, что при воздействии на пружинный
маятник вынуждающей силы груз совершает установившиеся гармонические колебания с
частотой этой силы.
Слайд 63
Вынужденные колебания
Так как амплитуда – положительная величина, то
выражение (4) имеет смысл, когда круговая частота вынуждающей силы
ω меньше собственной круговой частоты системы ω˳ (ω˂ω˳). В этом случае колебания системы происходят в одной фазе с колебаниями силы.
Если ω˃ω˳, то колебания системы происходят в противофазе с колебаниями силы (ϕ= -π), а для амплитуды смещения берут модуль выражения (4).
4
Слайд 64
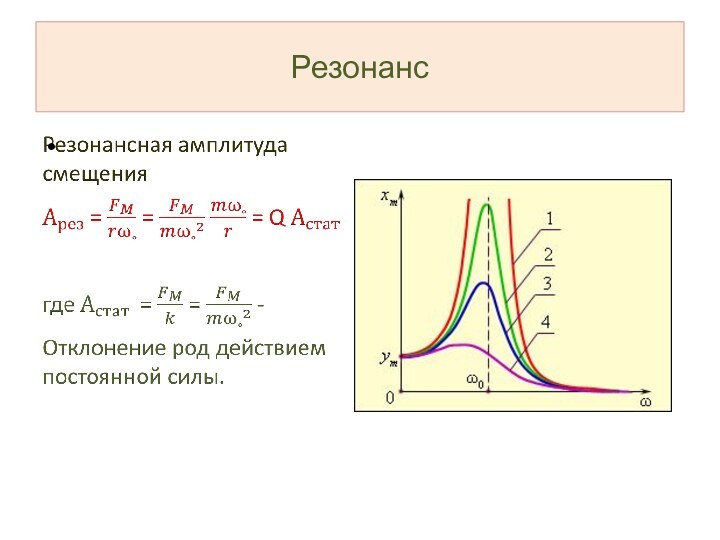
Резонанс
При совпадении частоты вынуждающей силы с собственной частотой
системы (ω = ω˳) выражение (4) теряет смысл, ибо
делить на нуль нельзя.
При ω→ω˳ А →∞ что не имеет физического смысла.
Это означает, что в данном случае нельзя пренебрегать затуханием.
Случай, когда частота вынуждающей силы совпадает с собственной частотой колебательной системы, называется резонансом.
Слайд 66
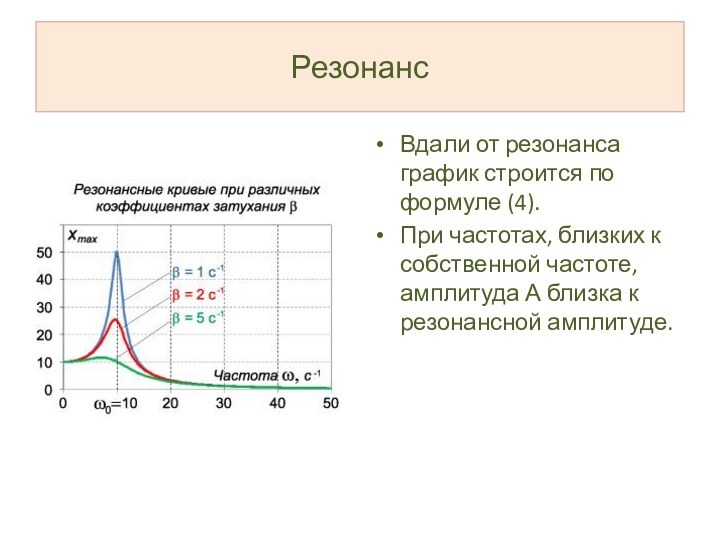
Резонанс
Вдали от резонанса график строится по формуле (4).
При
частотах, близких к собственной частоте, амплитуда А близка к
резонансной амплитуде.
Слайд 67
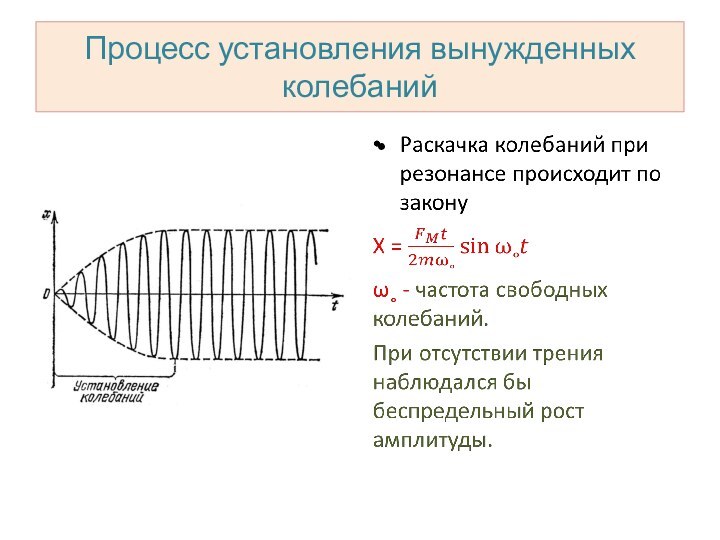
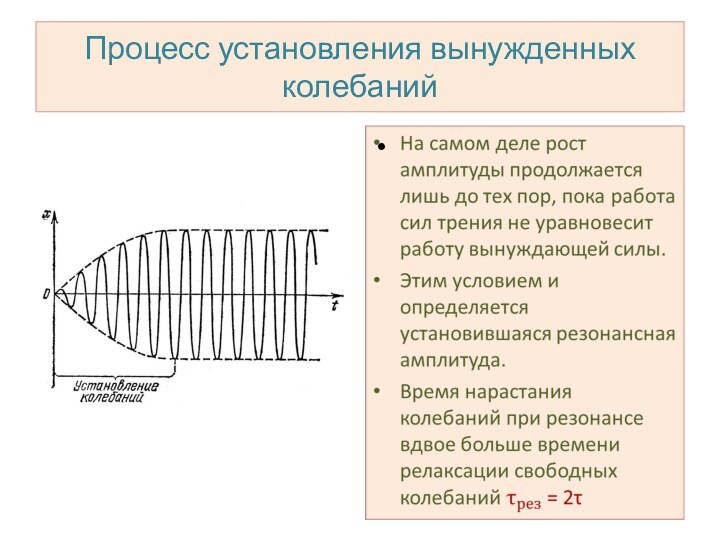
Процесс установления вынужденных колебаний