Слайд 2
Введение
Анализ логических схем можно рассматривать
как процедуру выявления рисков сбоя из-за различного вида состязаний
сигналов (процедуру оценки функциональной устойчивости схем). Сравним существующие методы анализа. Для этого оценим в самом общем случае сложность анализа схем на риск сбоя.
Если на вход комбинационной схемы подается n переменных, то на нем могут действовать 2n наборов, от каждого из которых может осуществляться переход к 2n - 1 набору, то есть всего будет существовать 2n(2n - 1) переходов. При n = 4 число переходов приблизительно представляется как 22n.
Время анализа: количество переменных n = 64; ЭВМ способна проанализировать один переход между двумя наборами за 1 мкс. Время анализа в данном случае будет составлять 10-6 2128 секунд или приблизительно 1025 лет.
Слайд 3
Методы анализа КС на риски сбоя
Широкое распространение получили
следующие методы:
- использование временных диаграмм, в том числе асинхронное
моделирование на их основе ;
- графический метод Хаффмена ;
- использование многозначной логики, для которой, как и для булевой алгебры, справедливы принципы ассоциативности и коммутативности;
- использование двоичной алгебры;
- получают развитие методы, основанные на аппарате дифференциальных булевых уравнений;
…..
Слайд 4
Методы анализа КС на риски сбоя
Временные диаграммы являются
эффективным средством анализа переходных процессов в цифровых схемах. Временные
диаграммы являются основой при выполнении асинхронного моделирования, однако этот метод требует представления схемы по многоярусной структуре, поэтому не всегда выявляет риски сбоя.
Графический метод Хаффмена разработан для анализа схем с небольшим числом переменных. Анализ проводится по картам Карно и графам переходов наборов. Однако с ростом числа переменных, от которых зависит функция алгебры логики, этот метод становится практически неприемлемым из-за графической громоздкости.
Слайд 5
Методы анализа КС на риски сбоя
Методы многозначной логики
основаны на использовании кроме значений 0 и 1 булевой
алгебры различных представлений событийных сигналов:
- при трехзначном моделировании для представления значений величин сигналов берется множество L = {0, 1/2, 1} , где 0 и 1 интерпретируются так же, как и в булевой алгебре, а 1/2 используется для представления событийного (переходного) процесса. Значение 1/2 воспринимается логическим элементом либо как 0, либо как 1, то есть если некоторый сигнал изменяет свое значение, то в течение переходного процесса значение сигнала может восприниматься как 0 или как 1, поэтому при моделировании оно обозначается как 1/2, причем это обозначение надо рассматривать как единый символ;
- четырехзначная модель (алгебра Поста): 0, переходы 01 и 10, 1;
- пятизначная модель: 0, 01, 10, 1, Х – неопределенное значение;
Слайд 6
Методы анализа КС на риски сбоя
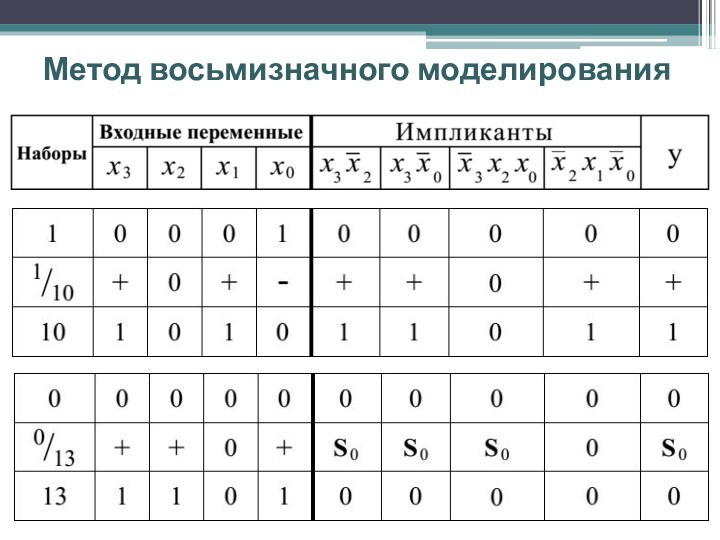
- восьмизначная модель:
0, 1, чисто алгоритмические переходы 01 и 10, которые
обозначаются специальными символами “+” и “–” соответственно, статические риски сбоя S0 и S1, динамические риски сбоя D+ и D–;
- девятизначная модель: к символам восьмизначной модели добавляется символ “неопределенное значение”, под которым понимают случайное значение выхода RS – триггера, когда на его входах совершается переход от запрещенного набора к набору, соответствующему режиму хранения. Этот метод применяется для анализа на риски сбоя схем с памятью или с обратными связями.
Все методы многозначного моделирования достаточно сложны для ручного применения и рассчитаны в основном для проведения анализа схем на ЭВМ. Для ручного применения используют методы трехзначного и восьмизначного моделирования и только для сравнительно простых схем.
Слайд 7
Методы анализа КС на риски сбоя
Особенностью метода, использующего
двоичную алгебру, является возможность определения не только факта наличия
рисков сбоя в схеме на заданных входных переходах, но и вычисления количества возможных ложных переходов на выходах схемы.
В методах, основанных на аппарате дифференциальных булевых уравнений, в булевы функции непосредственно вводится дискретная временная функция, а изменение булевых функций во времени оценивается с помощью производной функции по времени. Алгоритм выполнения анализа схем с помощью этого метода достаточно сложен, но позволяет выявлять соотношения задержек в состязающихся цепях, которые определяют наличие или отсутствие сбоя, то есть возможно получение рекомендаций для корректировки влияния состязаний.
Слайд 8
Метод трехзначного моделирования
Так как логическая функция задается
для трехзначного моделирования в виде системы булевых уравнений, необходимо
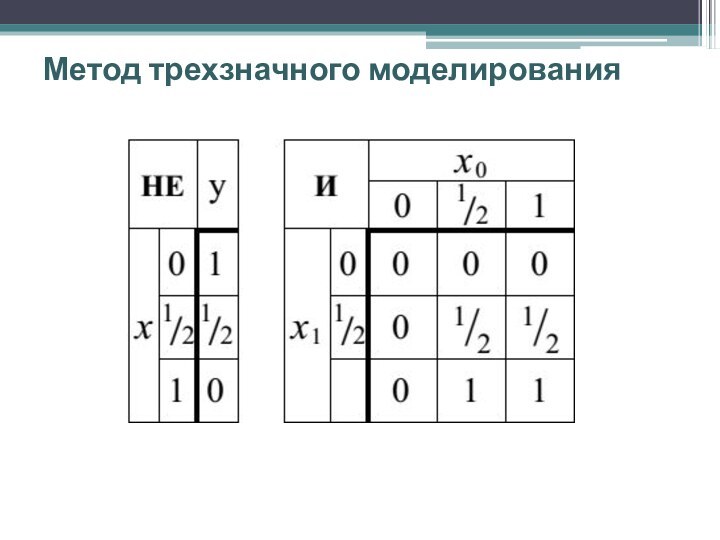
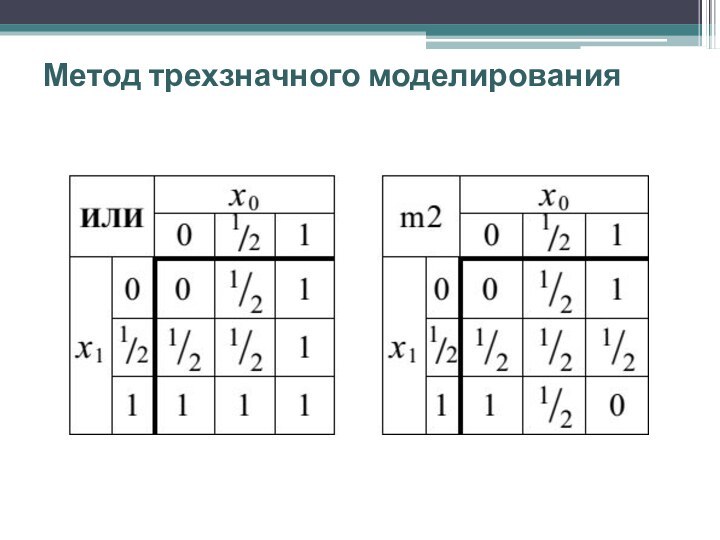
определить троичные функции выходов основных булевых элементов НЕ, И, ИЛИ и “сумма по модулю 2”
Трехзначные функции определяются на множестве L так:
В табл. приведены выходные сигналы для основных логических элементов, на входах которых действуют трехзначные сигналы.
Слайд 9
Метод трехзначного моделирования
Слайд 10
Метод трехзначного моделирования
Слайд 11
Метод трехзначного моделирования
Пусть на схему, имеющую n входов,
последовательно подаются два входных набора Х1 = an-1,..., ai,...,
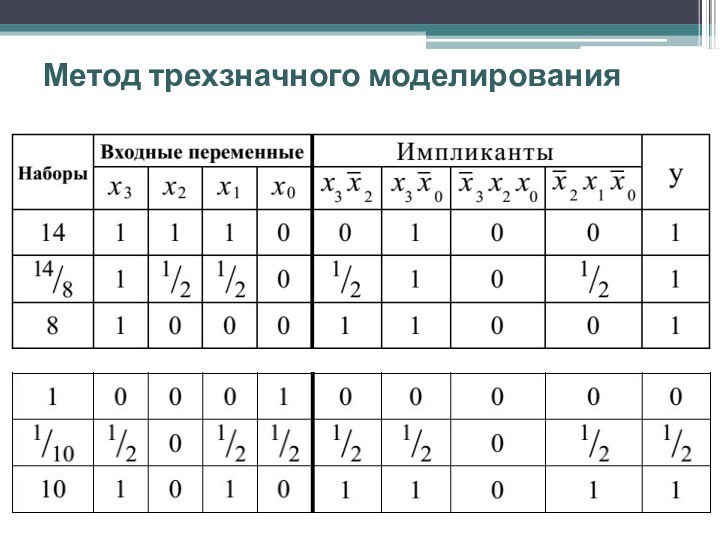
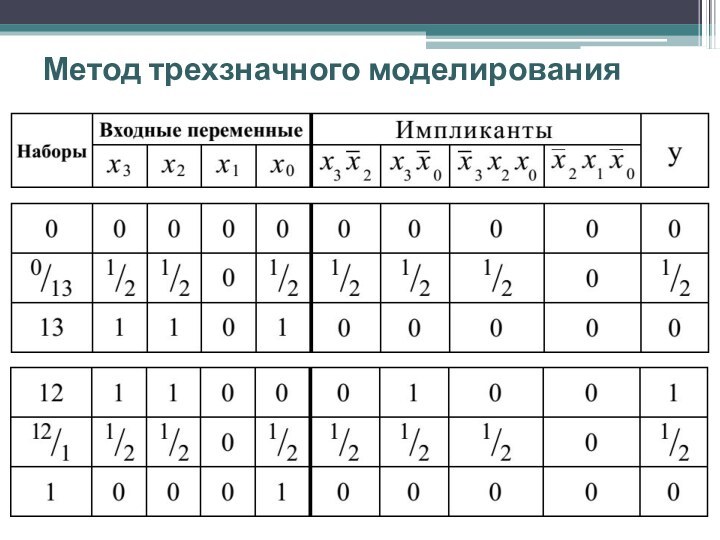
a0 и Х2 = bn-1,..., bi,..., b0. Тогда переходный вектор Х1/Х2 имеет следующий вид: Х1/Х2 = cn-1,..., ci,..., c0, где ci = 1/2, если ai bi и ci = ai, если ai = bi при i= 0, 1, 2 ,..., n-1.
Если при моделировании для некоторых последовательных наборов Х1 и Х2 зафиксировано, что y(Х1) = y(Х2), а y(Х1/Х2) = 1/2, то схема содержит статический риск сбоя.
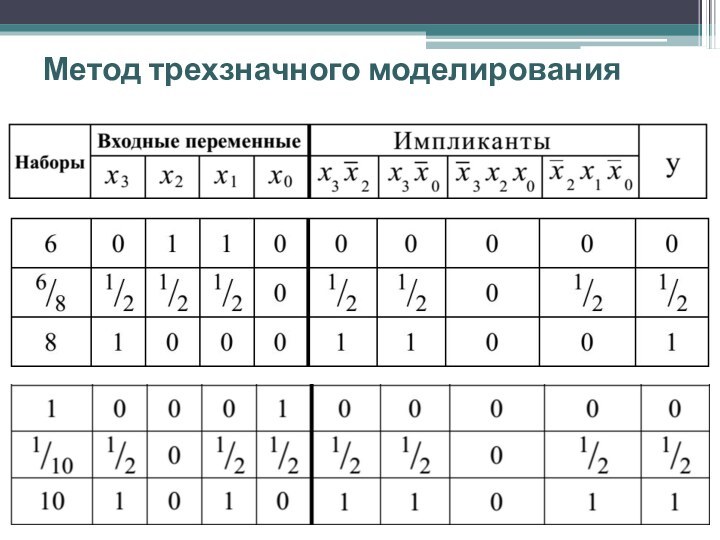
Проанализируем работу схемы, которая реализует функцию:
Для следующих переходов:
Слайд 12
Метод трехзначного моделирования
Слайд 13
Метод трехзначного моделирования
Слайд 14
Метод трехзначного моделирования
Слайд 15
Метод восьмизначного моделирования
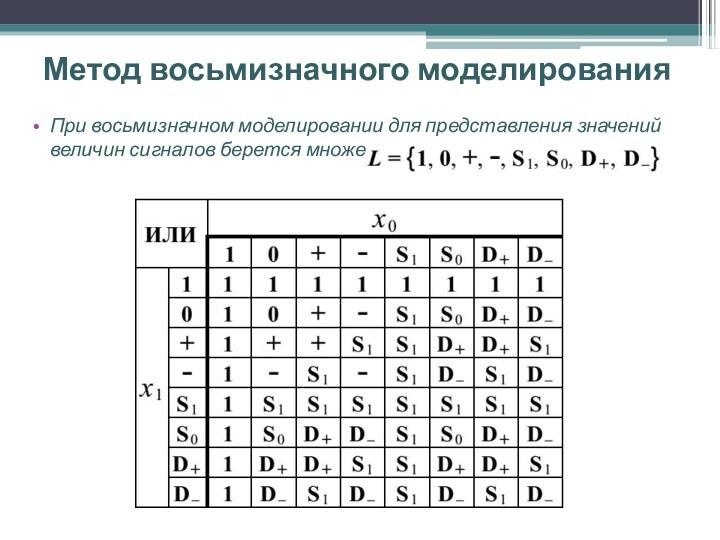
При восьмизначном моделировании для представления значений
величин сигналов берется множество:
Слайд 16
Метод восьмизначного моделирования
При восьмизначном моделировании для представления значений
величин сигналов берется множество:
Слайд 17
Метод восьмизначного моделирования
При восьмизначном моделировании для представления значений
величин сигналов берется множество:
Слайд 18
Метод восьмизначного моделирования
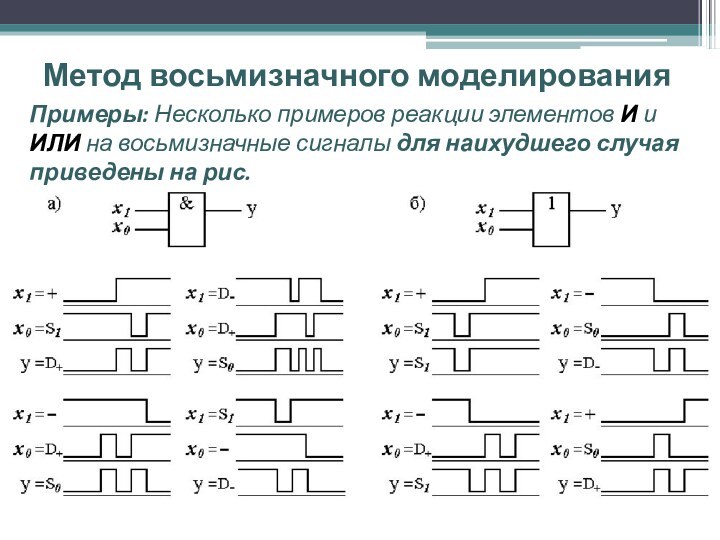
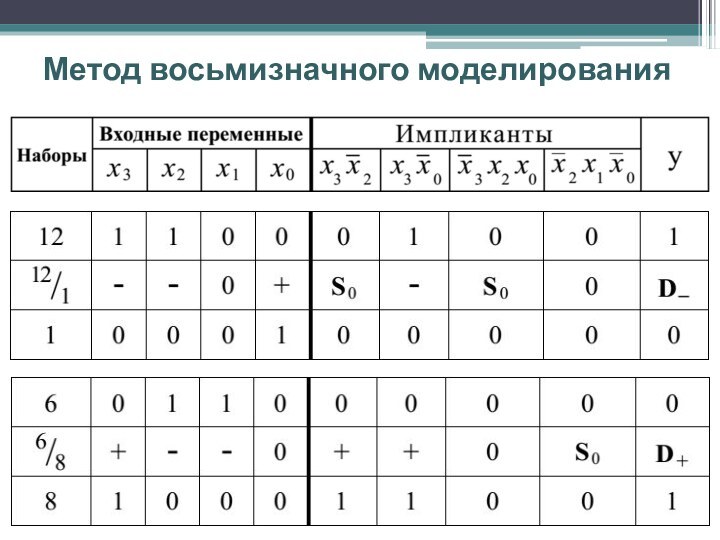
Примеры: Несколько примеров реакции элементов И
и ИЛИ на восьмизначные сигналы для наихудшего случая приведены
на рис.
Слайд 19
Метод восьмизначного моделирования
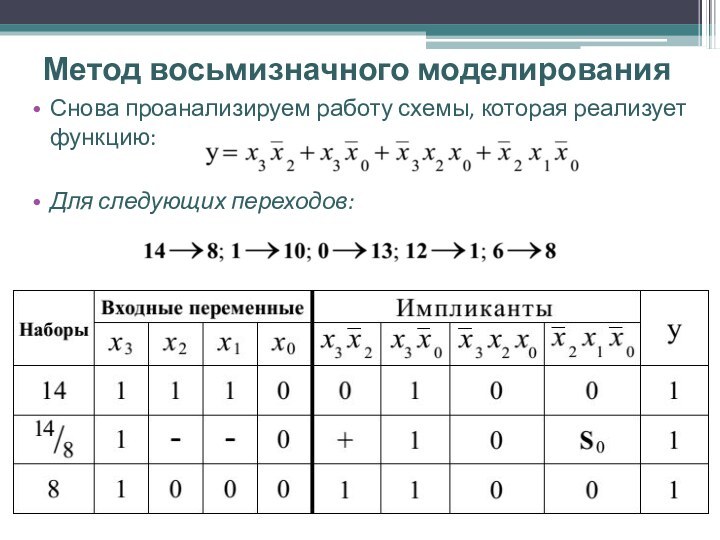
Снова проанализируем работу схемы, которая реализует
функцию:
Для следующих переходов:
Слайд 20
Метод восьмизначного моделирования
Слайд 21
Метод восьмизначного моделирования
Слайд 22
Достоинства метода многозначной логики
!!! Рассмотренный метод
восьмизначной логики нагляден, удобен, применим и для ручного, и
для машинного анализа.
Слайд 24
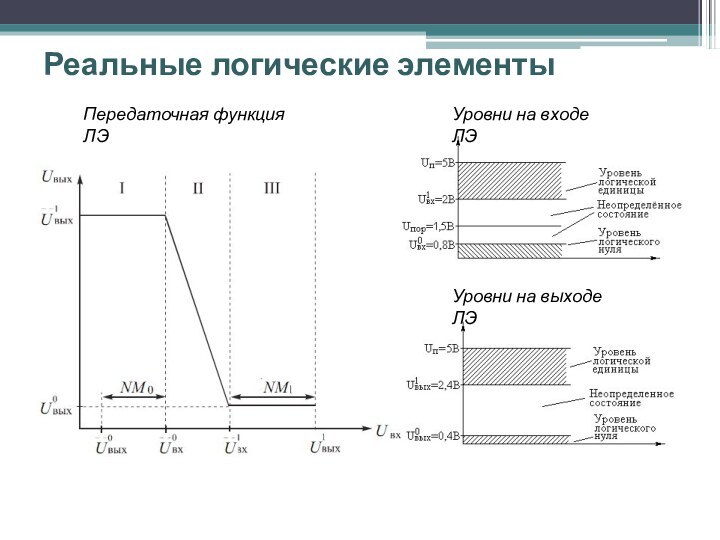
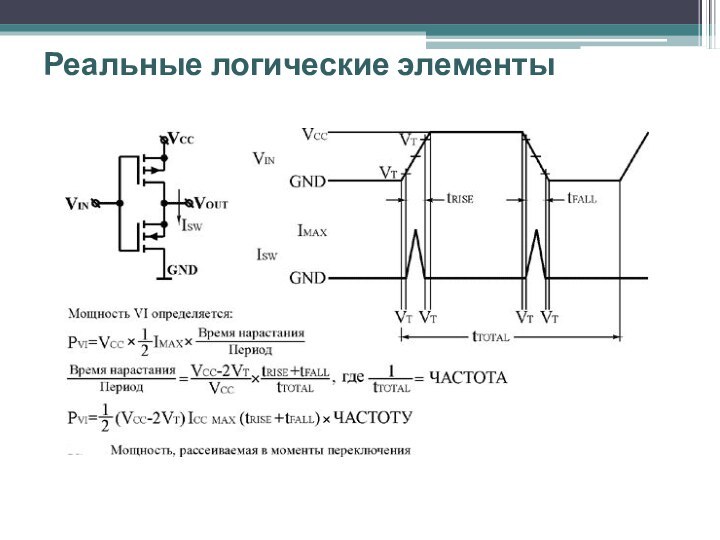
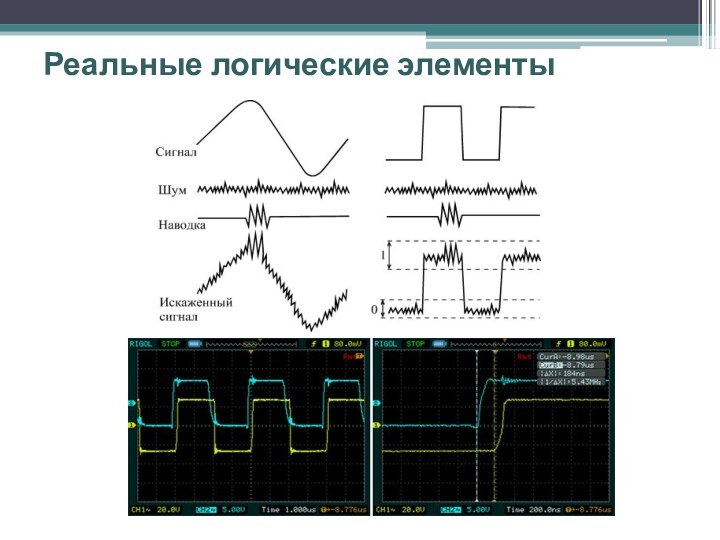
Реальные логические элементы
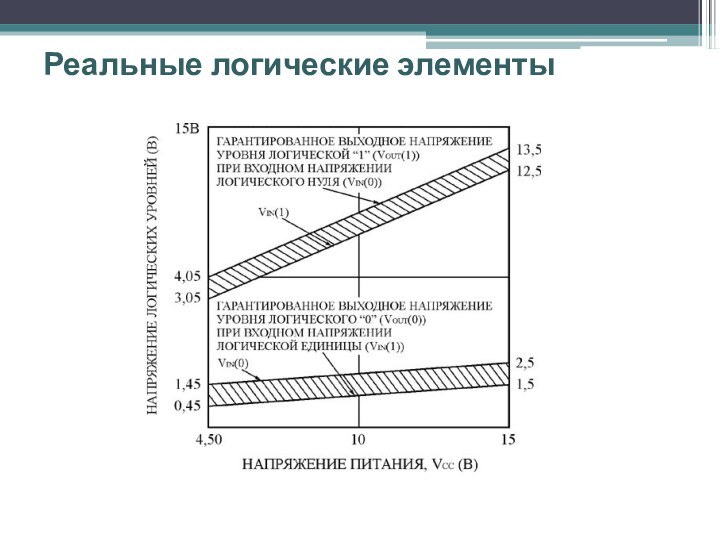
Уровни на входе ЛЭ
Уровни
на выходе ЛЭ
Передаточная функция ЛЭ
Слайд 28
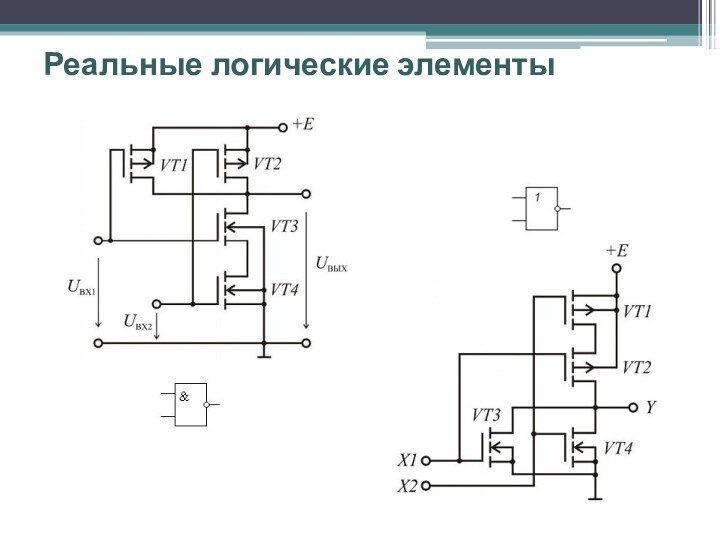
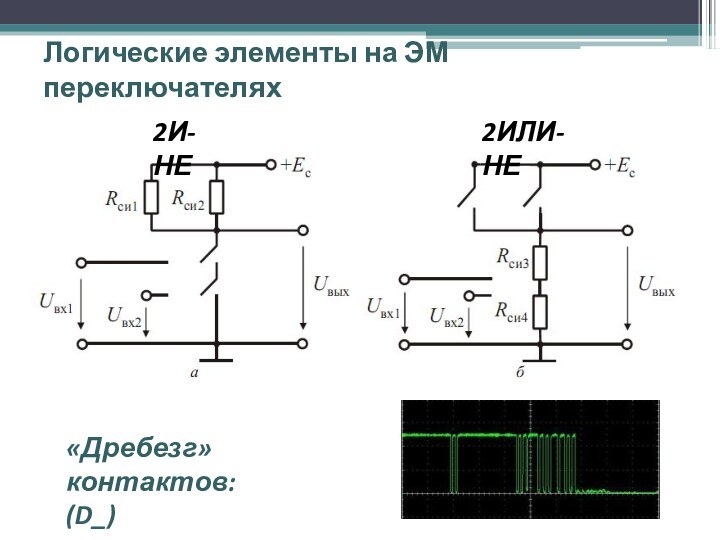
Логические элементы на ЭМ переключателях
2И-НЕ
2ИЛИ-НЕ
«Дребезг» контактов:
(D_)
Слайд 30
Риски сбоя в комбинационных схемах
Определения:
Риск сбоя -
возможность появления на выходе цифрового устройства сигнала, не предусмотренного
алгоритмом его работы и могущего привести к ложному срабатыванию.
РИСК СБОЯ ? ЭТО НАИХУДШИЙ СЛУЧАЙ!!
Функциональная устойчивость определяется стабильностью реализации цифровым устройством заданного алгоритма работы при наличии разброса задержек выполнения операций в логических элементах, задержек сигналов в линиях связи и эл
ектромагнитных наводок паразитных сигналов.
Синоним “функциональной устойчивости” - алгоритмическая устойчивость.
Слайд 31
Риски сбоя в комбинационных схемах
Определения:
Состязания (гонки) сигналов
- процесс распространения сигналов в различных цепях цифрового устройства
при существовании разбросов временных задержек этих цепей.
Цепь - совокупность логических и других элементов и линий связи между ними.
Алгоритмический переход - изменение сигнала на выходе какой-либо схемы, предусмотренное алгоритмом ее работы.
Неалгоритмический переход - изменение выходного сигнала, не предусмотренное алгоритмом ее работы.
Опасные состязания - которые могут привести в цифровой схеме к неалгоритмическому переходу при заданных условиях ее работы.
Слайд 32
Риски сбоя в комбинационных схемах
Определения:
Неопасные состязания –
которые не могут привести в схеме к неалгоритмическому переходу
при заданных условиях ее работы.
Схема, свободная от влияния опасных состязаний - цифровая структура, в которой неалгоритмический переход, возникший в части схемы из-за опасных состязаний, не изменяет алгоритма работы схемы в целом при заданных условиях ее работы.
Опасными состязаниями (гонками) по входу – называют неодновременное переключение логических элементов, при одновременном изменении сигнала на их входах, связанное с тем, что логические элементы изготовленные в различных технологических циклах имеют различные параметры. При различных пороговых входных напряжениях получаем неодновременное срабатывание логических элементов.
Слайд 33
Риски сбоя в комбинационных схемах
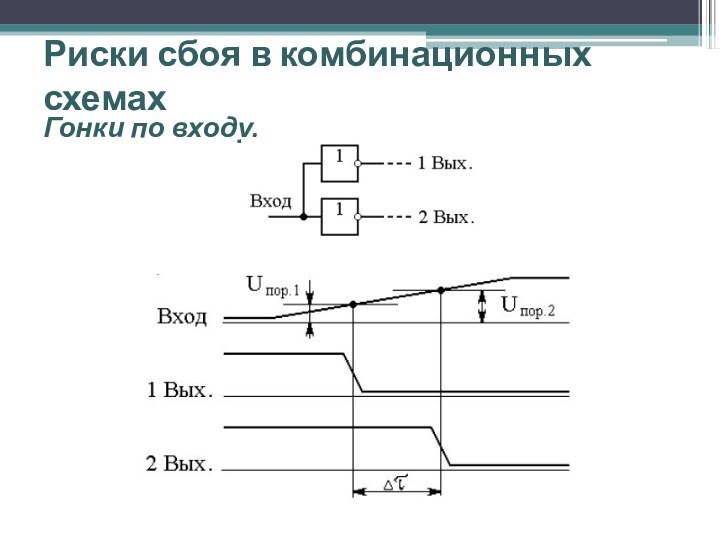
Гонки по
входу.
Слайд 34
Риски сбоя в комбинационных схемах
Определения:
Изменение сигнала на
каждом выходе схемы реально происходит не мгновенно, а образует
некоторый сложный динамический процесс.
Нахождение этих процессов называется динамическим анализом комбинационной схемы.
Динамический анализ учитывает обстоятельства:
Изменение входного набора схемы состоит из неодновременных изменений различных входных переменных, образующих этот набор. (последовательность входных наборов можно рассматривать как набор входных нулей и единиц, действующих независимо друг от друга на разных входах.
Помимо логических элементов в схеме могут иметься специальные вспомогательные элементы – задержки
Каждый инерционный логический элемент в большинстве случаев можно представить в виде модели, содержащей последовательное соединение безынерционного ЛЭ с элементом задержки (иногда фильтром) на ‘τ’
Слайд 35
Риски сбоя в комбинационных схемах
Определения:
Изменение сигнала на
каждом выходе схемы реально происходит не мгновенно, а образует
некоторый сложный динамический процесс.
Нахождение этих процессов называется динамическим анализом комбинационной схемы.
Динамический анализ учитывает обстоятельства:
Изменение входного набора схемы состоит из неодновременных изменений различных входных переменных, образующих этот набор. (последовательность входных наборов можно рассматривать как набор входных нулей и единиц, действующих независимо друг от друга на разных входах.
Помимо логических элементов в схеме могут иметься специальные вспомогательные элементы – задержки
Каждый инерционный логический элемент в большинстве случаев можно представить в виде модели, содержащей последовательное соединение безынерционного ЛЭ с элементом задержки (иногда фильтром) на ‘τ’
Слайд 36
Риски сбоя в комбинационных схемах
Определения:
Переключательный процесс -
последовательность уровней “1” и “0” (импульсов и пауз), которая
на любом конечном наблюдаемом интервале времени содержит конечное число переходов 01 и 10.
Длиной переключательного процесса называется общее число изменений сигнала в нем. Например, для процесса x4 на рис. 2 длина равна 3.
Переключательный процесс сложный - если его длина >2, в случае если длина <2 - простое переключение.
Векторный переключательный процесс считается простым переключением, если все его компоненты - простые переключения, совершаемые одновременно. В противном случае векторный процесс считается сложным.
Слайд 37
Риски сбоя в комбинационных схемах
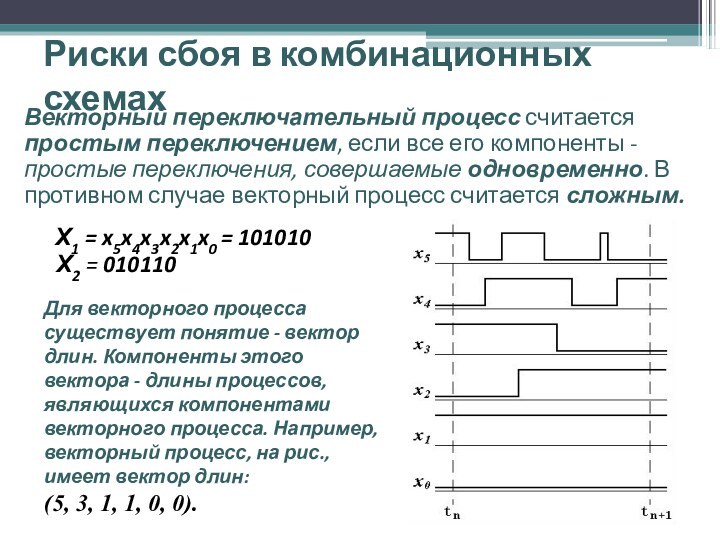
Векторный переключательный процесс считается
простым переключением, если все его компоненты - простые переключения,
совершаемые одновременно. В противном случае векторный процесс считается сложным.
Х1 = x5x4x3x2x1x0 = 101010
Х2 = 010110
Для векторного процесса существует понятие - вектор длин. Компоненты этого вектора - длины процессов, являющихся компонентами векторного процесса. Например, векторный процесс, на рис., имеет вектор длин:
(5, 3, 1, 1, 0, 0).
Слайд 38
Риски сбоя в комбинационных схемах
Событие - любое изменение
логического сигнала, в том числе сложный переключательный процесс.
Различают два
вида задержек:
чистая задержка, которая при подаче на вход сигнала x(t) обусловливает на выходе сигнал y(t–τ), где τ – величина задержки
инерционная задержка или фильтр - осуществляет ту же операцию, что и чистая задержка, но сверх того не пропускает на выход изменений входного сигнала, отстоящих одно от другого по времени менее чем на ‘τ’, благодаря чему процесс на выходе может изменить форму.
Слайд 39
Риски сбоя в комбинационных схемах
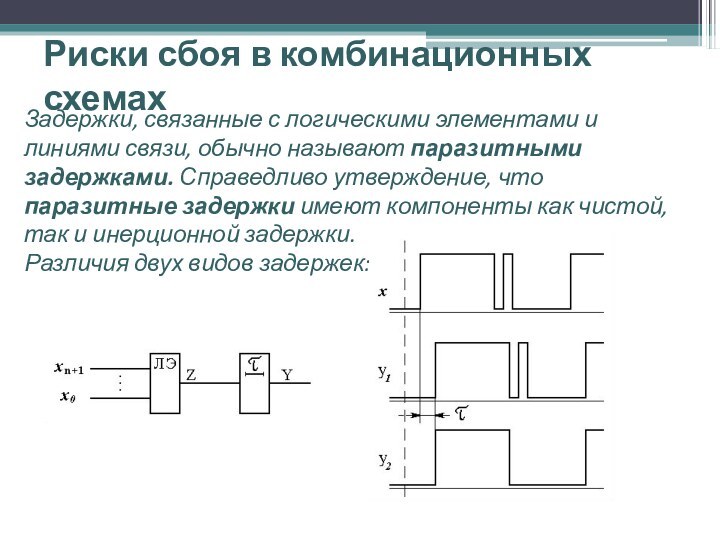
Задержки, связанные с логическими
элементами и линиями связи, обычно называют паразитными задержками. Справедливо
утверждение, что паразитные задержки имеют компоненты как чистой, так и инерционной задержки.
Различия двух видов задержек:
Слайд 40
Риски сбоя в комбинационных схемах
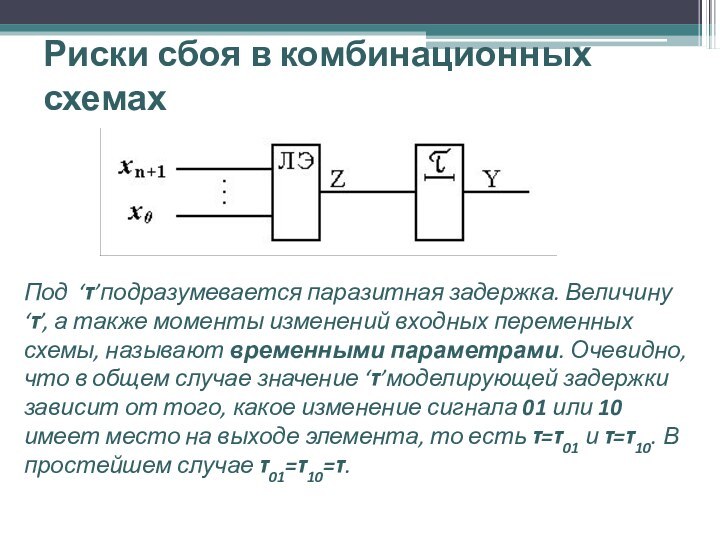
Под ‘τ’подразумевается паразитная задержка.
Величину ‘τ’, а также моменты изменений входных переменных схемы,
называют временными параметрами. Очевидно, что в общем случае значение ‘τ’моделирующей задержки зависит от того, какое изменение сигнала 01 или 10 имеет место на выходе элемента, то есть τ=τ01 и τ=τ10. В простейшем случае τ01=τ10=τ.
Слайд 41
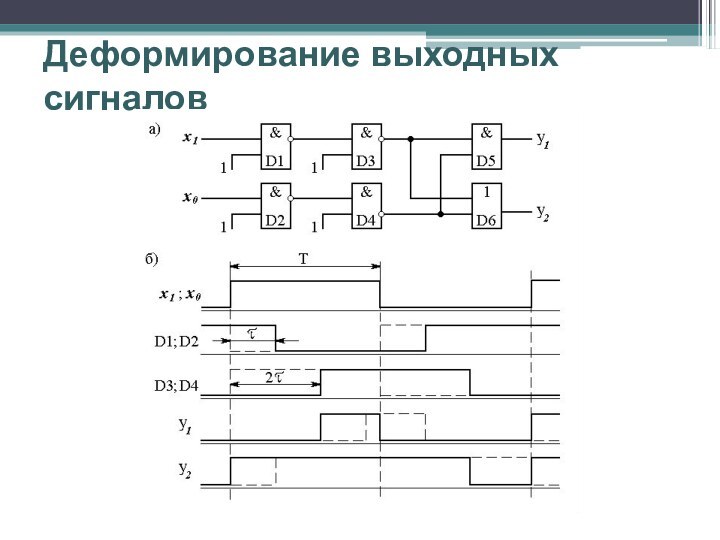
Деформирование выходных сигналов
В различных частях комбинационной схемы в
зависимости от числа последовательно включенных элементов переходный процесс после
смены входного набора будет заканчиваться в разное время. Это приведет либо к деформированию длительности выходных сигналов либо к появлению рисков сбоя.
Если сигналы в схеме распространяются по цепочкам, задержки в которых различны, то это приводит к смещению сигналов относительно друг друга во времени. В свою очередь, это может вызвать уменьшение длительности сигнала “1” на выходе элемента И и увеличение - на выходе ИЛИ.
Деформирование выходного сигнала может привести к исчезновению алгоритмически верного сигнала!!!
.
Слайд 42
Деформирование выходных сигналов
Слайд 43
Статические риски сбоя
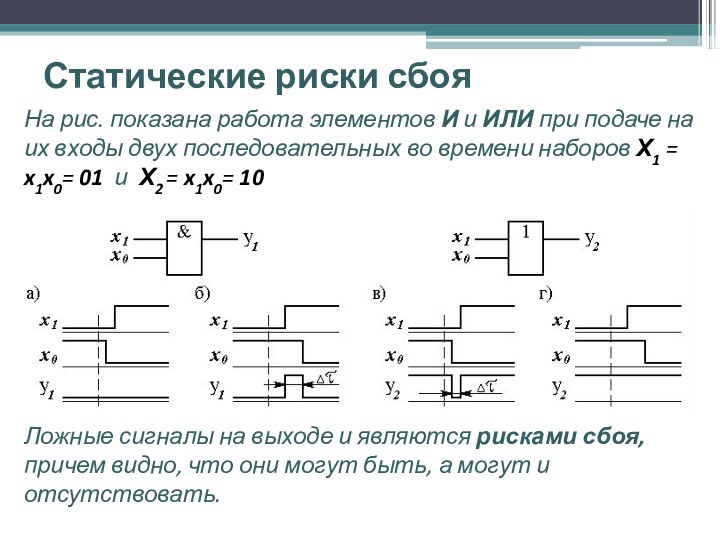
На рис. показана работа элементов И
и ИЛИ при подаче на их входы двух последовательных
во времени наборов Х1 = x1x0= 01 и Х2 = x1x0= 10
Ложные сигналы на выходе и являются рисками сбоя, причем видно, что они могут быть, а могут и отсутствовать.
Слайд 44
Статические риски сбоя
Риск сбоя называется статическим, если у(X1)
= y(Х2), где y - булева функция. Риск сбоя
называется статическим в нуле S0, если у(X1) = y(Х2) = 0. Риск сбоя называется статическим в единице S1, если у(X1) = y(Х2) = 1.
На рис. б имеет место статический риск сбоя в нуле S0, а на рис. в - статический риск сбоя в единице S1.
Слайд 45
Динамические риски сбоя
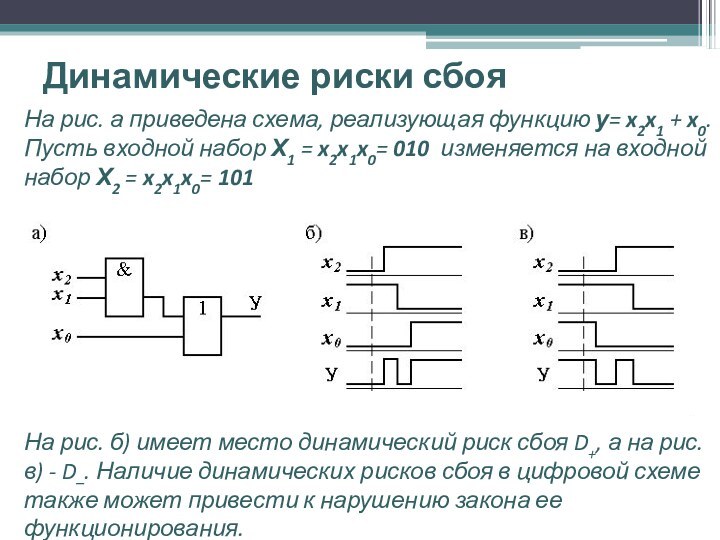
На рис. а приведена схема, реализующая
функцию у= x2x1 + x0. Пусть входной набор Х1
= x2x1x0= 010 изменяется на входной набор Х2 = x2x1x0= 101
На рис. б) имеет место динамический риск сбоя D+, а на рис. в) - D–. Наличие динамических рисков сбоя в цифровой схеме также может привести к нарушению закона ее функционирования.
Слайд 46
Динамические риски сбоя
Риск сбоя называется динамическим, если у(X1)
≠ y(Х2), где y - булева функция. Риск сбоя
называется динамическим D+ при переходе на выходе 01, если у(X1) = 0, а y(Х2) = 1. Риск сбоя называется динамическим D– , если у(X1) = 1, а y(Х2) = 0.
Слайд 47
Логический риск сбоя
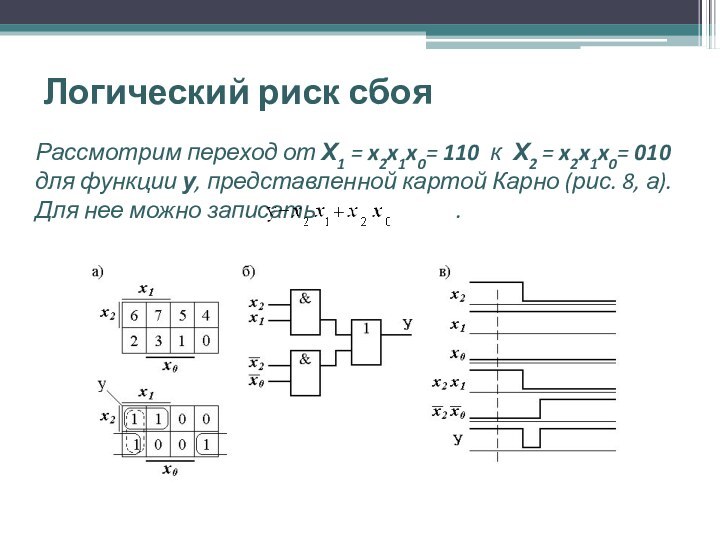
Рассмотрим переход от Х1 = x2x1x0=
110 к Х2 = x2x1x0= 010 для функции у,
представленной картой Карно (рис. 8, а). Для нее можно записать .
Слайд 48
Логический риск сбоя
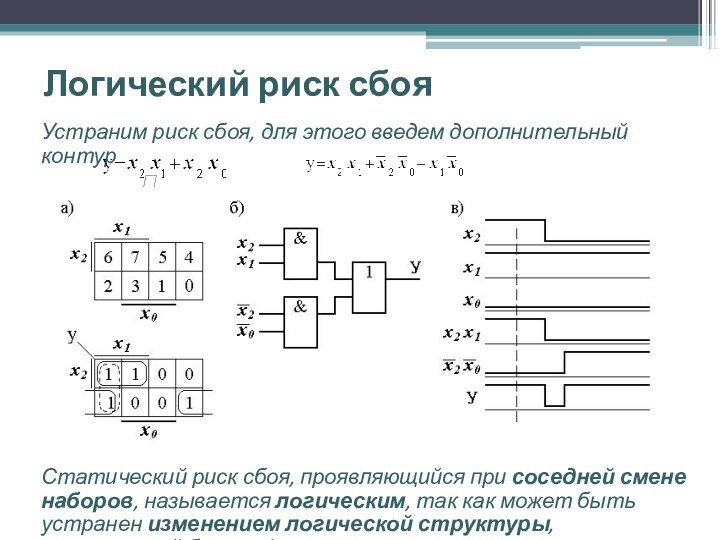
Устраним риск сбоя, для этого введем
дополнительный контур
?
Статический риск сбоя, проявляющийся при соседней смене наборов,
называется логическим, так как может быть устранен изменением логической структуры, реализующей булеву функцию
Слайд 50
Функциональный риск сбоя
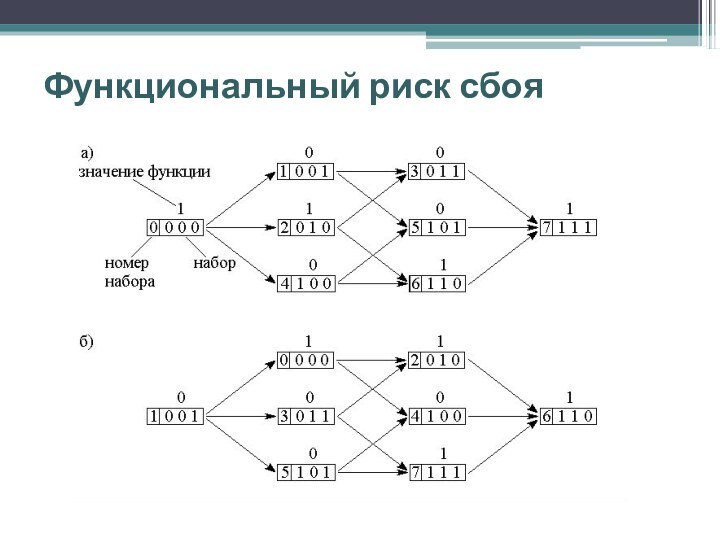
Есть единственный путь смены наборов: 0
2 6 7, при котором не будет статического риска
сбоя, так как у(X1 = 0) = y(Х2 = 7) = 1. Во всех остальных случаях будет статический риск сбоя в единице S1, причем никакими аппаратными средствами устранить его нельзя, так как значения выхода на промежуточных наборах определяются характером самой функции. Аналогично для рис б) - имеет место динамический риск сбоя D+, который также определяется характером самой функции.
Риски сбоя, проявляющиеся при многоместной смене наборов и определяемые характером самой функции, называются функциональными. Такие риски сбоя не могут быть устранены изменением логической структуры, реализующей булеву функцию.
Слайд 52
Минимизация функций алгебры логики
На практике решается более простая
задача представления ФАЛ в дизъюнктивной или конъюнктивной форме, содержащей
наименьшее возможное число букв (например, для СДНФ -- как можно меньше слагаемых, являющихся элементарными произведениями, которые содержат как можно меньше сомножителей). канонической задачей минимизации ФАЛ
Задачу минимизации ФАЛ можно разложить на этапы:
1) Переход от СДНФ к сокращенной ДНФ
2) Переход от сокращенной ДНФ к тупиковой ДНФ (ТДНФ), сокращением лишних импликант.
3) Переход от ТДНФ к минимальной форме.
Слайд 53
Методы минимизации ФАЛ
1) Расчетный метод –
метод непосредственных
преобразований;
2) Метод Квайна;
3) Расчетно-табличный
метод
(метод Квайна – Мак’Класски);
4) Метод Петрика;
5) Табличный метод (метод карт Карно);
6) Метод неопределенных коэффициентов;
7) Метод гиперкубов;
8) Метод факторизации;
9) Метод функциональной декомпозиции;
…
Слайд 54
Табличный метод
В данном методе применяются
или диаграммы Вейча или карты Карно, которые отличаются друг
от друга расположением столбцов и строк.
В картах Карно порядок следования : 00 01 11 10.
В диаграммах Вейча порядок следования : 00 01 10 11.
Позиции наборов располагаются в соответствии с циклическим кодом Грея. Наборы соседние, если различаются только в одном разряде.
Эталонная и рабочая карты Карно для функции n=3:
y
Слайд 55
Правила минимизации для карт Карно
1. В карте
Карно группы единиц (ДНФ) необходимо покрыть контурами. Внутри контура
должны находится только единицы. (соответствует операции склеивания - нахождения импликант данной функции).
2. Количество единиц контура должно быть степенью двойки (1, 2, 4, 8, ...).
3. Каждый контур должен включать максимально возможное количество клеток. В этом случае он будет соответствовать простой импликанте.
4. Все единицы в карте (даже одиночные) должны быть охвачены контурами. Любая единица может входить в контуры произвольное количество раз.
5. Множество контуров, покрывающих все единицы функции, образуют тупиковую ДНФ.
6. В элементарной конъюнкции, которая соответствует одному контуру, остаются только те переменные, значение которых не изменяется внутри контура.
7. На основании закона тавтологии любая единичная клетка может быть включена в любое количество контуров, для получения минимальной ДНФ нужно стремиться к отсутствию лишних покрытий.
Слайд 56
Табличный метод
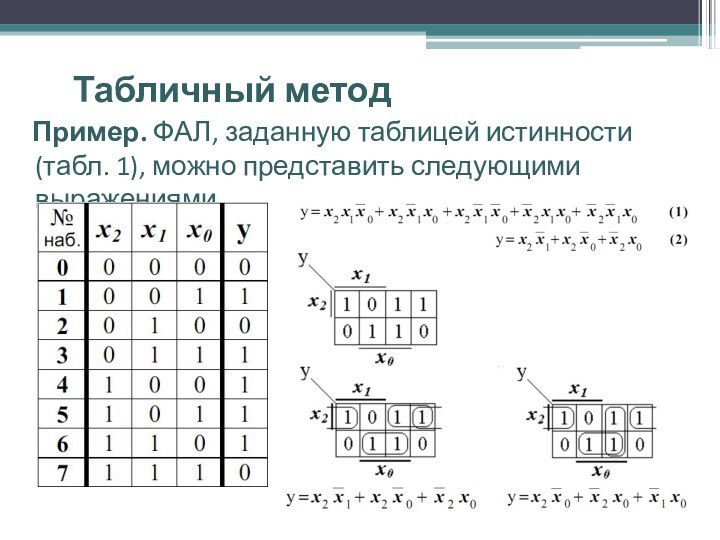
Пример. ФАЛ, заданную
таблицей истинности (табл. 1), можно представить следующими выражениями
Слайд 57
Эталонные карты Карно для n= 4, 5
Пример.
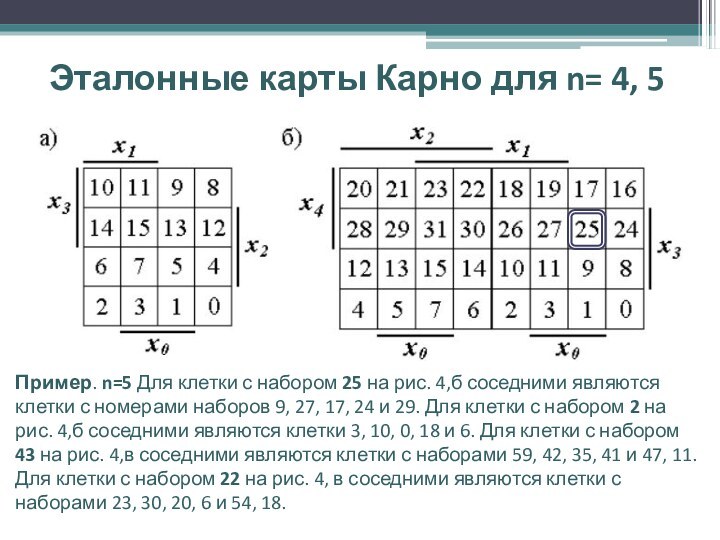
n=5 Для клетки с набором 25 на рис. 4,б
соседними являются клетки с номерами наборов 9, 27, 17, 24 и 29. Для клетки с набором 2 на рис. 4,б соседними являются клетки 3, 10, 0, 18 и 6. Для клетки с набором 43 на рис. 4,в соседними являются клетки с наборами 59, 42, 35, 41 и 47, 11. Для клетки с набором 22 на рис. 4, в соседними являются клетки с наборами 23, 30, 20, 6 и 54, 18.
Слайд 59
Минимизация на картах Карно для n= 4
y0=
Слайд 60
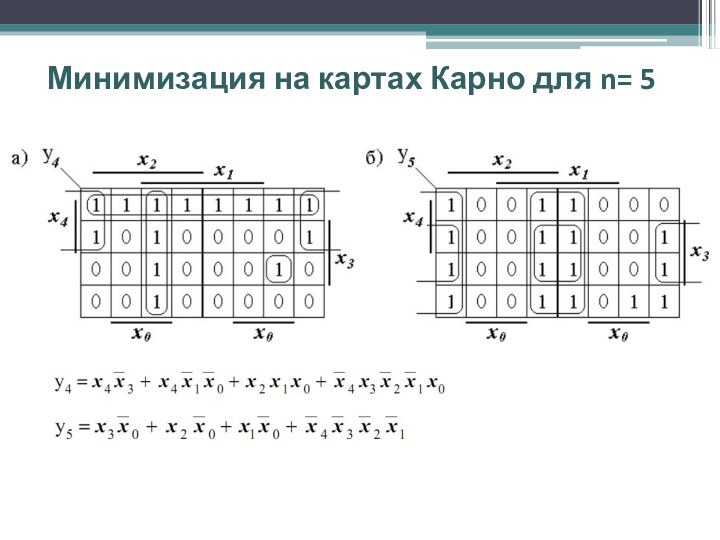
Минимизация на картах Карно для n= 5
Слайд 61
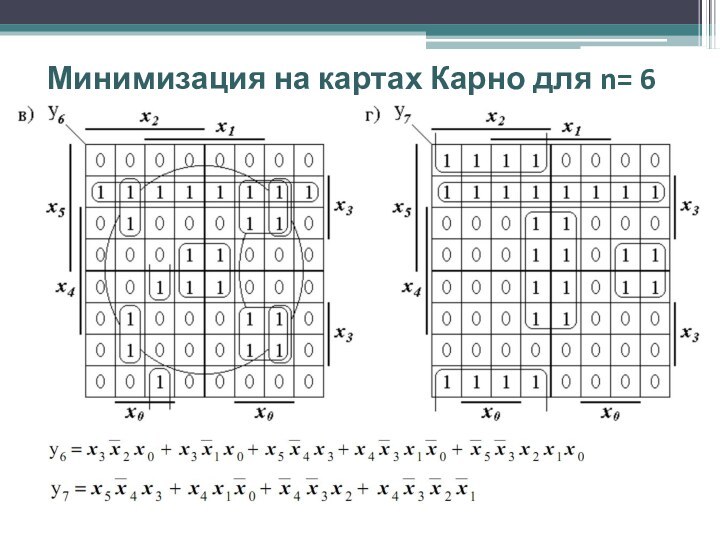
Минимизация на картах Карно для n= 6
Слайд 62
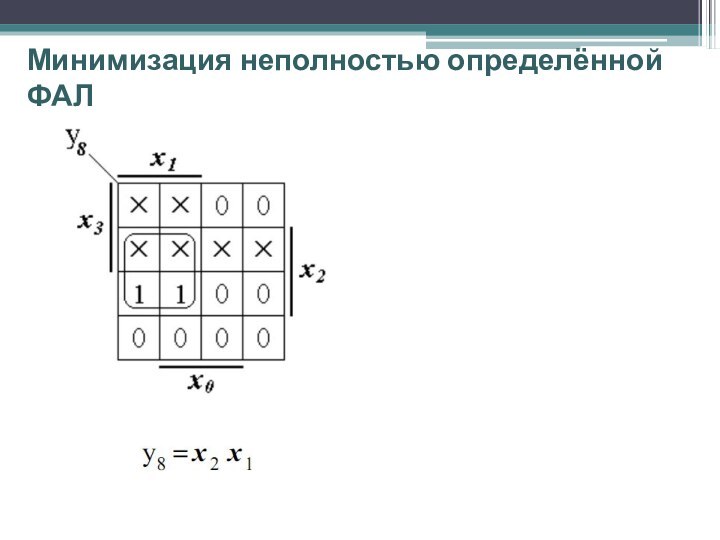
Минимизация неполностью определённой ФАЛ
Слайд 63
Достоинства и недостатки табличного метода минимизации ФАЛ
Достоинства:
1.

Основным достоинством применения карт Карно является компактность, простота и
наглядность представления полностью и неполностью определенных функций.
2. Их применение оправдано для n = 2 ÷ 6, а при определенных навыках даже для n = 7 и 8, что соответствует большинству реально встречающихся инженерных задач.
3. Карты Карно можно использовать для минимизации ФАЛ, заданных как в СДНФ, так и в СКНФ.
4. Удобно минимизировать системы булевых функций, так как на картах Карно легко выделять общие части реализуемой системы ФАЛ.
5. Легко находятся минимальные комбинации контуров по их виду на карте Карно.
6. Для построения карты Карно не обязательно задавать её в СДНФ или СКНФ (можно подставить значения наборов в любой вид ФАЛ и заносить значения ФАЛ на этом наборе в соответствующую клетку карты Карно).
7. Карты Карно сразу позволяют реализовать первые два этапа минимизации (склеивание и выявление лишних импликант).
Недостатки:
1. Затруднительно использовать карты Карно при n > 6.
2. Метод не является алгоритмически систематическим, многое зависит от навыков разработчика. Удобство обращения и экономия времени во многом зависит от его способности распознавать оптимальные конфигурации покрытия карт Карно.
Слайд 64
Метод Квайна-Мак’Класски
Метод состоит из последовательного выполнения
этапов:
1. Нахождение первичных импликант;
2. Расстановка меток;
3. Нахождение существенных импликант;
4. Вычеркивание лишних столбцов;
5. Вычеркивание лишних первичных импликант;
6. Выбор минимального покрытия максимальными
интервалами.
Слайд 65
Метод Квайна-Мак’Класски
Пусть минимизируемая функция задана в
СДНФ.
Элементарная коньюнкция ранга n = минитерм
ранга n.
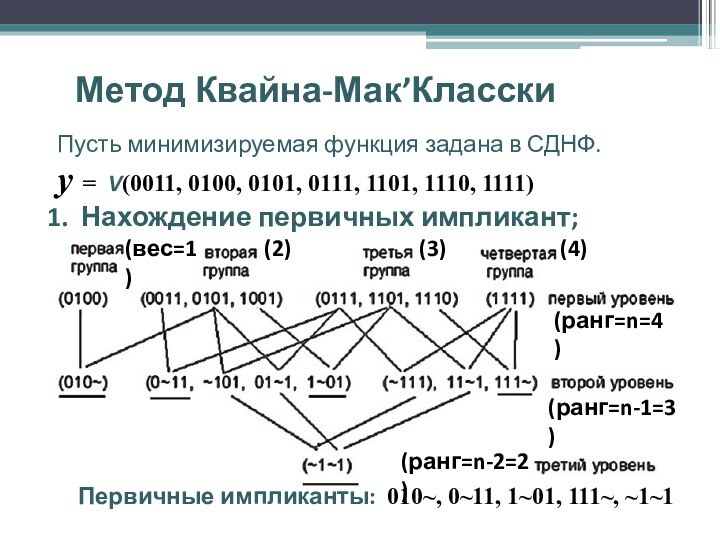
y = f (0011, 0100, 0101, 0111, 1101, 1110, 1111)
1. Нахождение первичных импликант;
Для всех минтермов функции определяют вес. Все минитермы функции, вес которых отличается на 1 попарно сравнивают. Записывают новый минитерм ранга n-1, на месте разряда с различными значениями записывают ~. Полученные минитермы ранга n-1 сравнивают попарно с учетом ~ и получают минитермы ранга n-2 и т.д. до тех пор пока это возможно. Минитермы для которых произошло склеивание отмечаются.
Все неотмеченные минитермы – первичные или простые импликанты.
Слайд 66
Метод Квайна-Мак’Класски
Пусть минимизируемая функция задана в
СДНФ.
y = V(0011, 0100, 0101, 0111, 1101, 1110,
1111)
1. Нахождение первичных импликант;
Первичные импликанты: 010~, 0~11, 1~01, 111~, ~1~1
(вес=1)
(2)
(3)
(4)
(ранг=n=4)
(ранг=n-1=3)
(ранг=n-2=2)
Слайд 67
Метод Квайна-Мак’Класски
Пусть минимизируемая функция задана в
СДНФ.
y = V(0011, 0100, 0101, 0111,
1101, 1110, 1111)
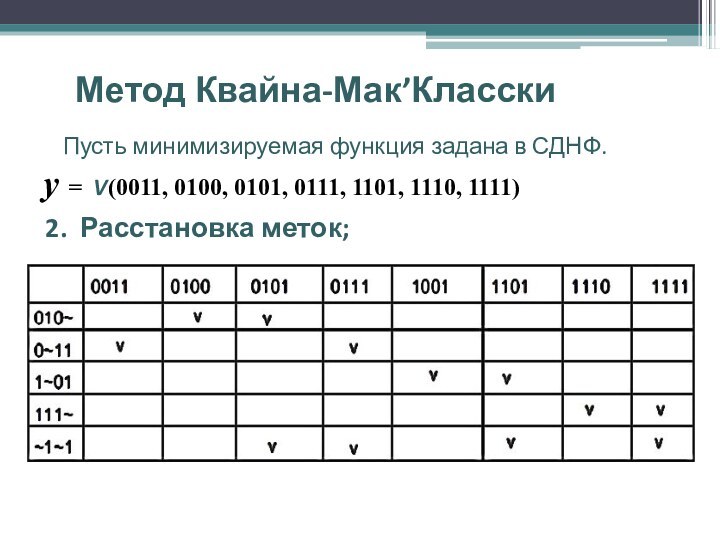
2. Расстановка меток;
Для данной функции = VMi ,
где Мi – простые импликанты полученные на первом этапе.
Для нахождения МДНФ нужно найти минимальное подмножество Мi, покрывающее коньюнкции исходной СДНФ.
Составляется таблица, строки - первичные импликанты минимизируемой функции, столбцы - исходные минитермы.
На пересечении ставится отметка, если первичная импликанта входит в соответствующий минитерм.
Слайд 68
Метод Квайна-Мак’Класски
Пусть минимизируемая функция задана в
СДНФ.
y = V(0011, 0100, 0101, 0111,
1101, 1110, 1111)
2. Расстановка меток;
Слайд 69
Метод Квайна-Мак’Класски
Пусть минимизируемая функция задана в
СДНФ.
y = V(0011, 0100, 0101, 0111,
1101, 1110, 1111)
3. Нахождение существенных импликант;
Если в столбце только одна метка, то первичная соответствующая импликанта – существенная.
Существенная импликанта не может быть исключена из результата, т.к. без нее не будет полного покрытия исходных минитермов.
Поэтому для сокращение размерности таблицы впоследствии вычеркивают строки с существенными импликантами и вычеркивают столбцы, которые они покрывают.
Существенные импликанты: 0~11, 010~, 1~01, 111~
Слайд 70
Метод Квайна-Мак’Класски
Пусть минимизируемая функция задана в
СДНФ.
y = V(0011, 0100, 0101, 0111,
1101, 1110, 1111)
3. Нахождение существенных импликант;
Существенные импликанты: 0~11, 010~, 1~01, 111~
Слайд 71
Метод Квайна-Мак’Класски
Пусть минимизируемая функция задана в
СДНФ.
y = V(0011, 0100, 0101, 0111,
1101, 1110, 1111)
4. Вычеркивание лишних столбцов;
Слайд 72
Метод Квайна-Мак’Класски
Пусть минимизируемая функция задана в
СДНФ.
y = V(0011, 0100, 0101, 0111,
1101, 1110, 1111)
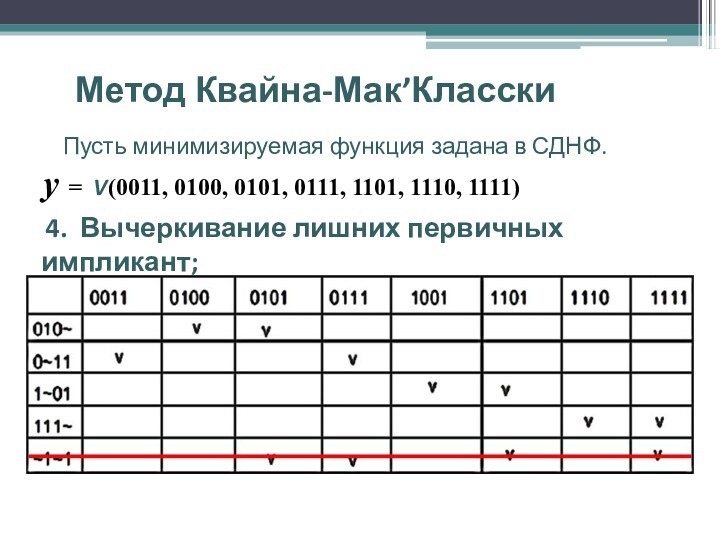
4. Вычеркивание лишних первичных импликант;
Слайд 73
Метод Квайна-Мак’Класски
Пусть минимизируемая функция задана в
СДНФ.
y = V(0011, 0100, 0101, 0111,
1101, 1110, 1111)
5. Выбор минимального покрытия максимальными интервалами;
Выбирается такая совокупность первичных импликант, которая включает метки во всех столбцах (как минимум, по одной в каждом столбце).
При нескольких возможных вариантах, предпочтение отдается варианту с минимальным суммарным числом переменных в простых импликантах, образующих покрытие.
!!! В приведенном примере самая короткая коньюнкция (~1~1), покрывающая наибольшее число минитермов, в решение не вошла.
Слайд 74
Метод Квайна-Мак’Класски
Пусть минимизируемая функция задана в
СДНФ.
y = V(0011, 0100, 0101, 0111,
1101, 1110, 1111)
5. Выбор минимального покрытия максимальными интервалами;
Тогда МДНФ: y = x3x2x1 + x3x1x0 + x3x1x0 + x3x2x1
Слайд 75
Метод Неопределенных коэффициентов
Метод состоит из последовательного выполнения этапов:
1. Представляем функцию
в виде ДНФ с неопределенными коэффициентами;
2. Задаем все возможные значения аргументов и приравниваем к полученному значению функции 0 или 1;
3. Составляем систему уравнений для коэффициентов и приравниваем, соответственно, к 0 или 1 значению функции;
4. Все коэффициенты в уравнениях с 0 значением функции также равны 0;
5. Вычеркиваем из уравнений с 1 значением функции все коэффициенты равные 0, из уравнений с 0 значениями ;
6. В полученных уравнениях оставляем коэффициенты с минимальным количеством индексов, которые присутствуют в максимальном количестве строк;
7. Выбираем минимальное покрытие в котором присутствуют коэффициенты с разными индексами, отсюда получаем МДНФ.
Слайд 76
Метод Неопределенных коэффициентов
Представление функции в СДНФ с неопределенными
коэффициентами:
Здесь представлены все возможные коньюнкции, которые могут входить в
ДНФ функции
Слайд 77
Метод Неопределенных коэффициентов
Система уравнений для определения значений
коэффициентов на различных наборах
:
Слайд 78
Метод Неопределенных коэффициентов
Пример:
Составляем систему:
Слайд 79
Метод Неопределенных коэффициентов
Из уравнений с 0 значениями
получаем:
Отсюда получаем МДНФ:
*
*