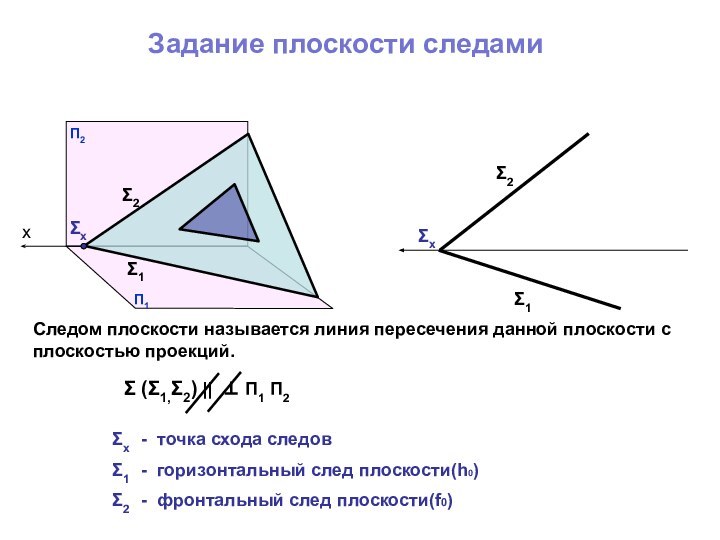
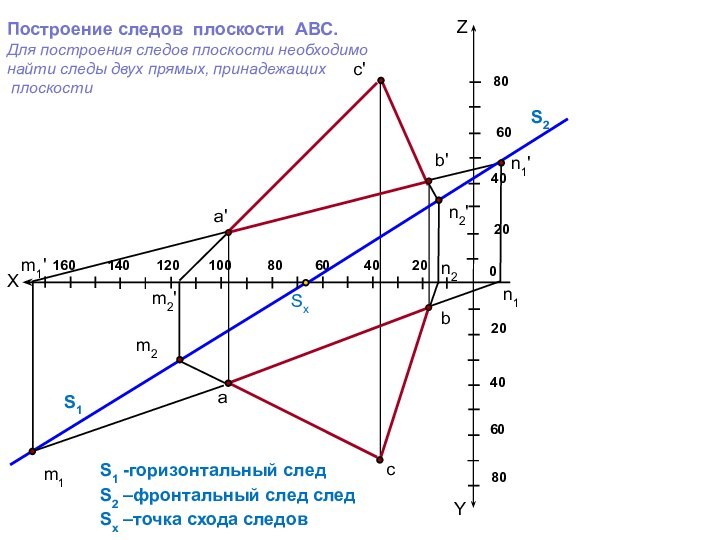
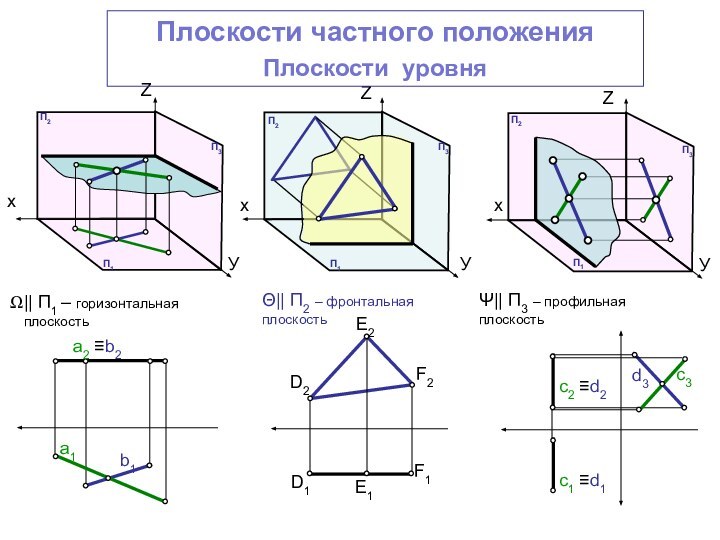
- горизонтальный след плоскости(h0)
2 - фронтальный след
плоскости(f0)х
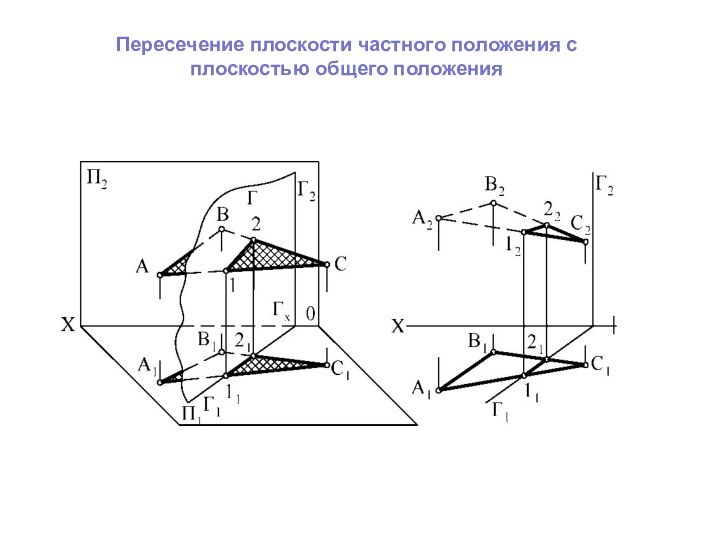
Следом плоскости называется линия пересечения данной плоскости с плоскостью проекций.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






![Плоскость 62C1Пересечение плоскостейа2b2а1b1A2B2C2A1B112223242Г211213141M1M2Г2152728251617181N1N2Дано:Σ= MN -?1. Г || П12. Г = [12]3. Г =](/img/tmb/13/1242500/dede01bb41dec3af8bac3cb4eec3d948-720x.jpg)
![Плоскость D22122F1A2B2C2C1B1A1F2D1E1Г2E21211M1M2323142411. [FE] Г2. ГΣ = [12]3. [12] ](/img/tmb/13/1242500/26f8eb0b882bf81b29c22fd648dfc2fe-720x.jpg)
![Плоскость 2141D222 62F1A2B2C2C1B1A1F2D1E1Г2E21211323142=521. [FE] Г2. ГΣ = [12]3. [12]](/img/tmb/13/1242500/88a1a2a15b9f2fbae159eb5b4fe19288-720x.jpg)
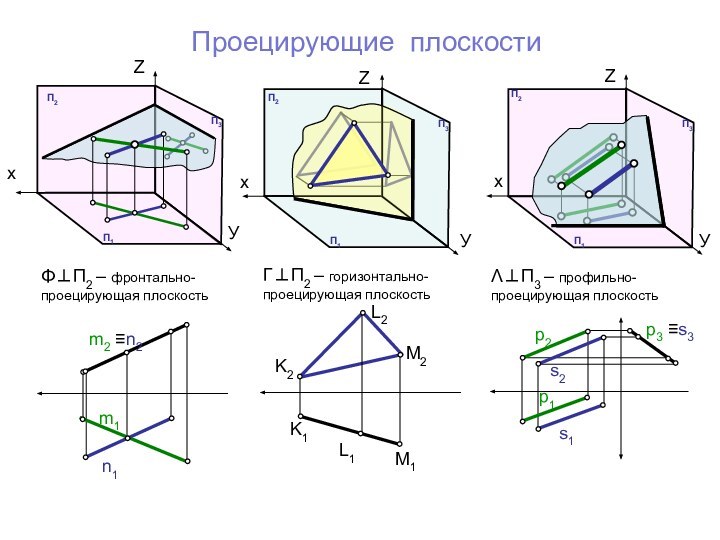
х
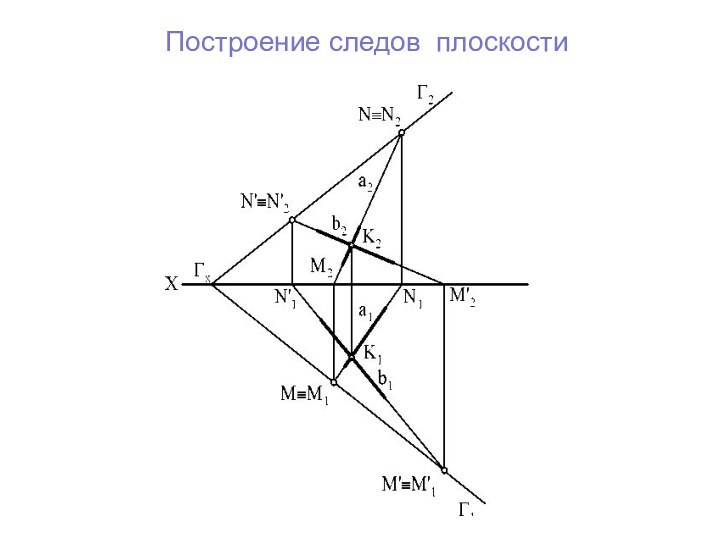
Следом плоскости называется линия пересечения данной плоскости с плоскостью проекций.
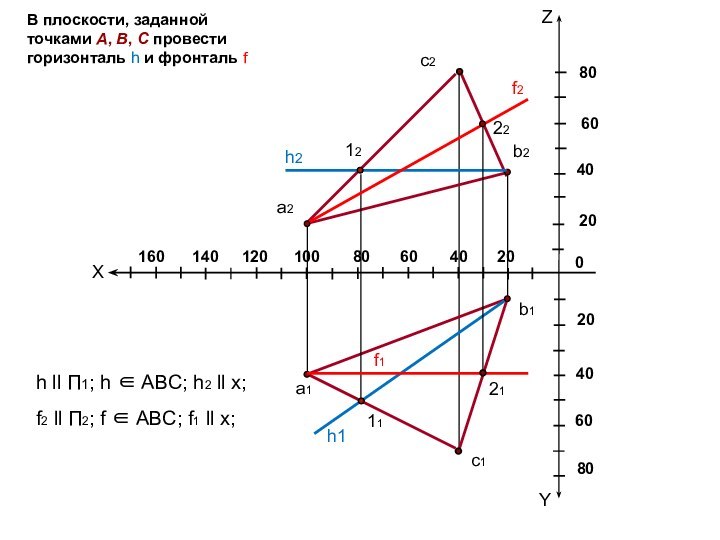
h1
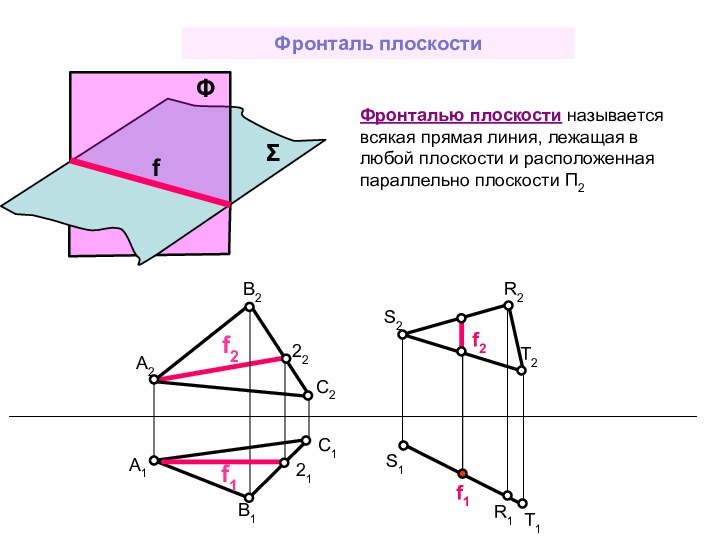
f2 ll П2; f ABC; f1 ll x;
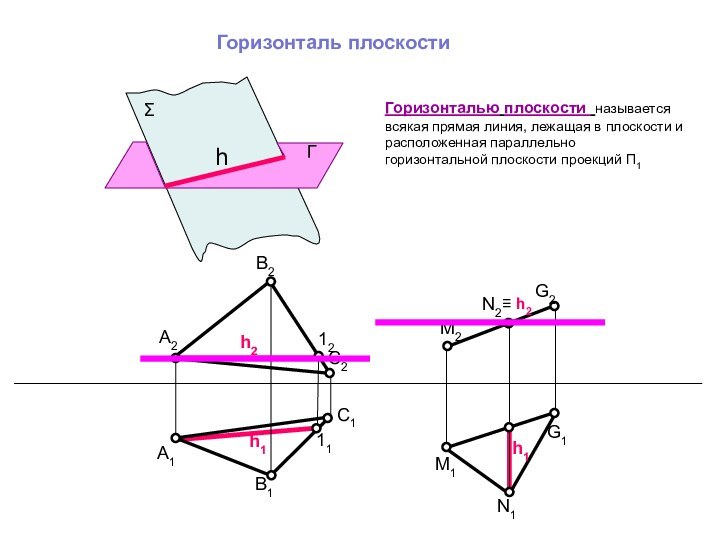
A1 D1a1
a Σ
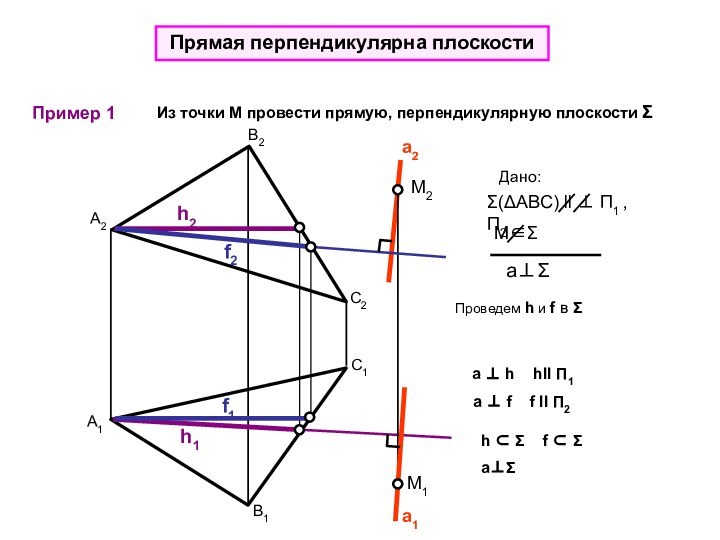
Дано:
a2
a1
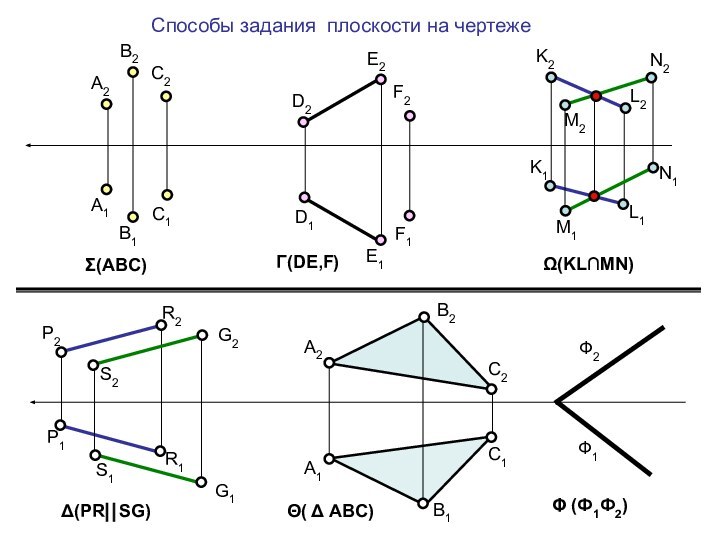
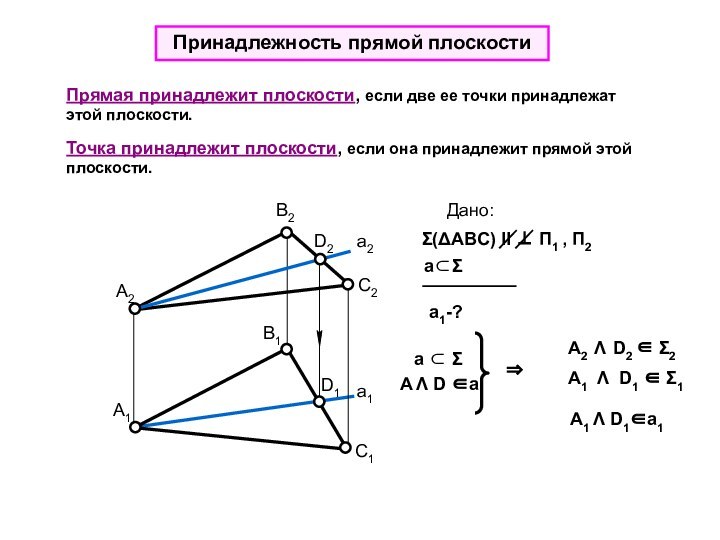
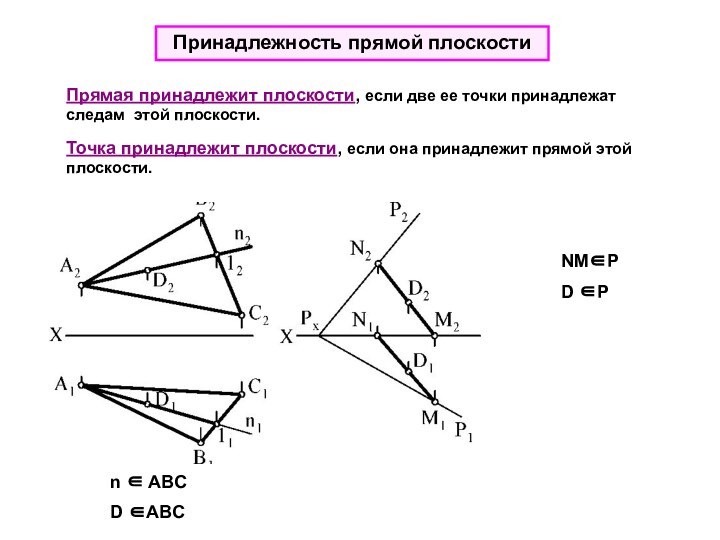
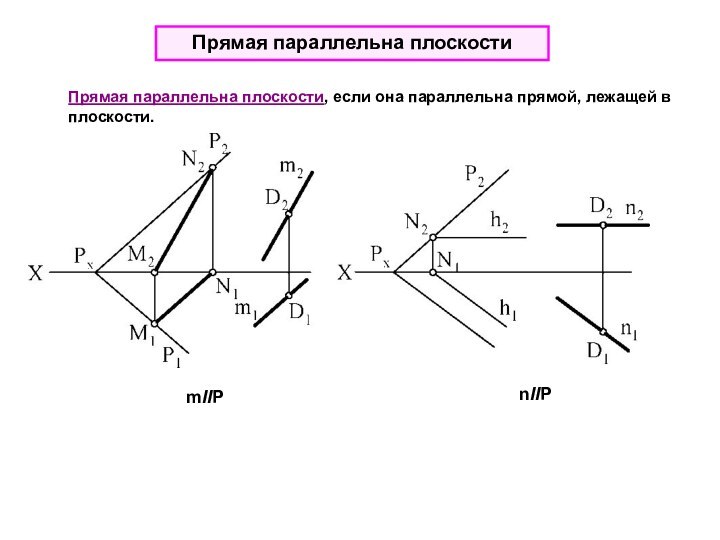
Точка принадлежит плоскости, если она принадлежит прямой этой плоскости.
A D a
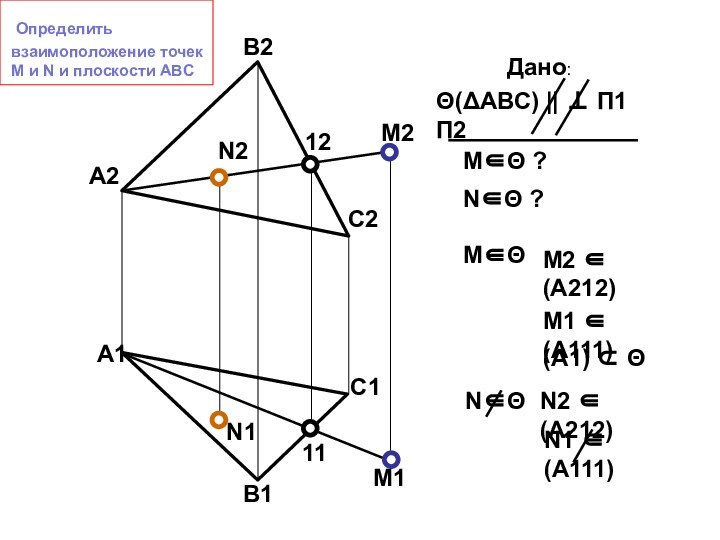
Дано:
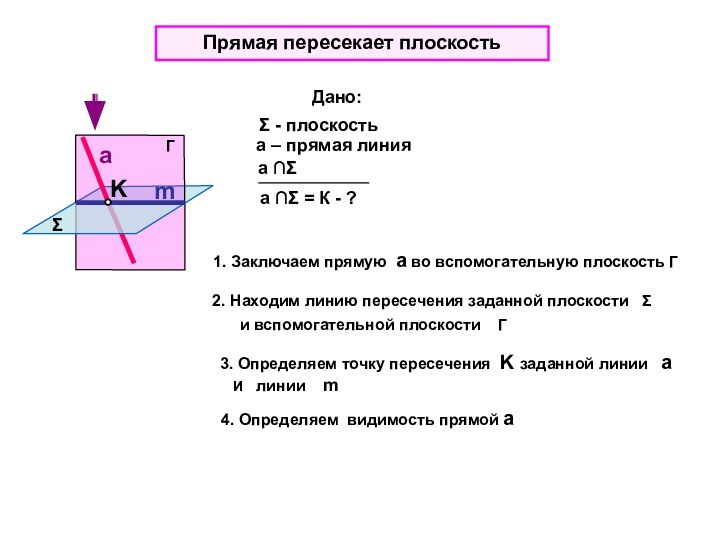
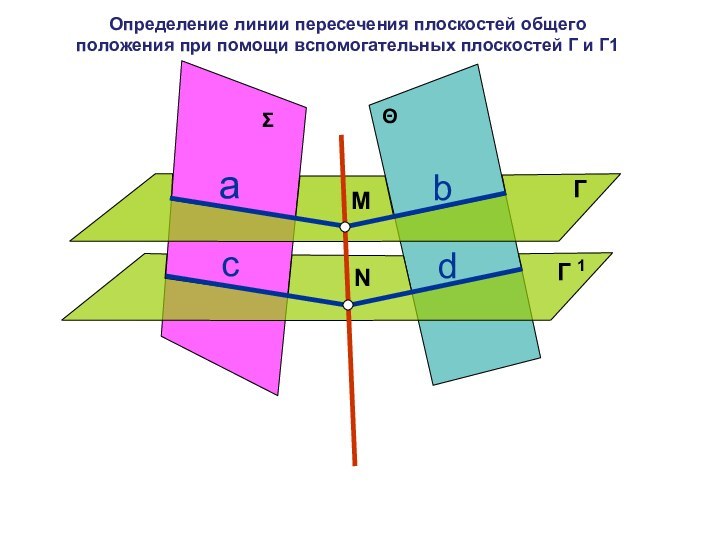
и вспомогательной плоскости Г
3. Определяем точку пересечения K заданной линии а
И линии m
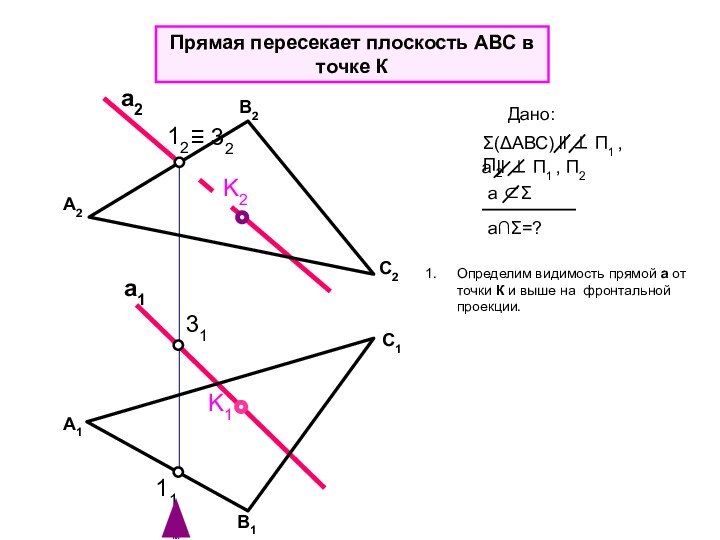
4. Определяем видимость прямой а
Дано:
Σ - плоскость
а – прямая линия
а Σ
3. m a = K
m Σ
Σ a = K
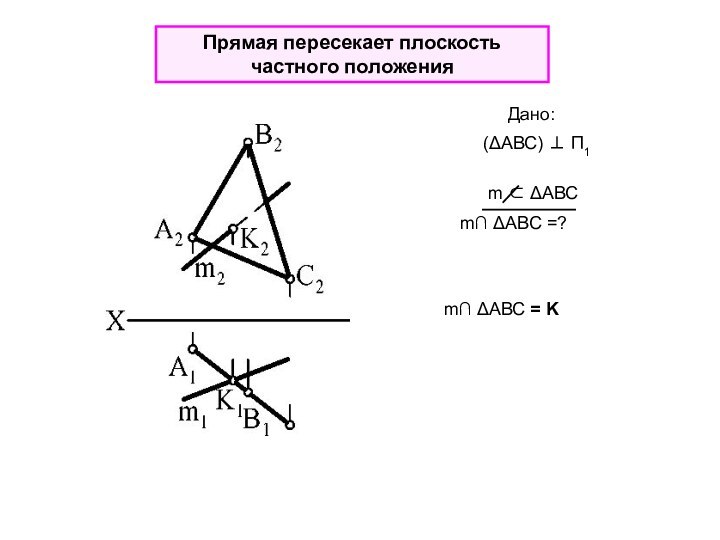
Дано:
aΣ=?
32
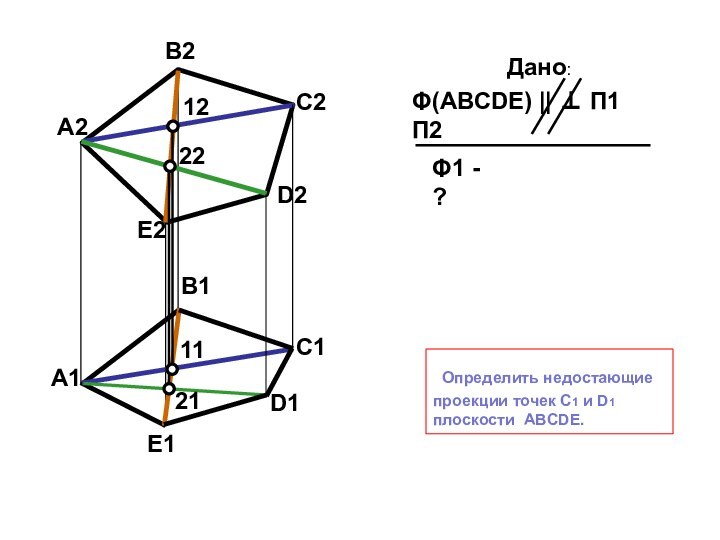
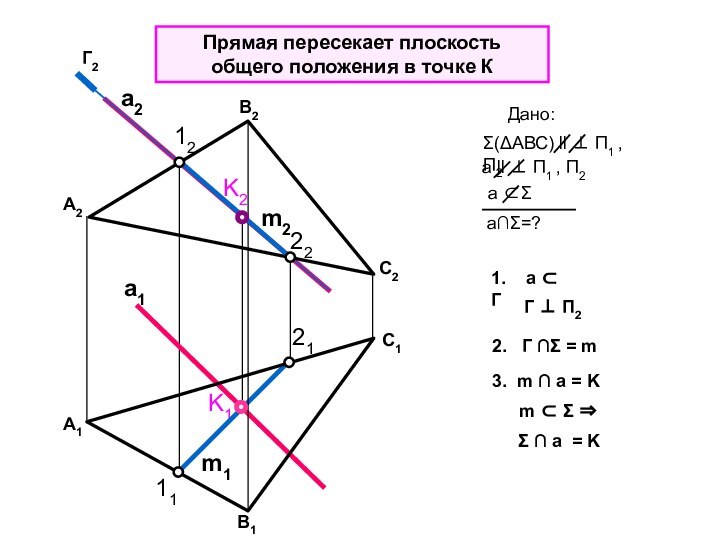
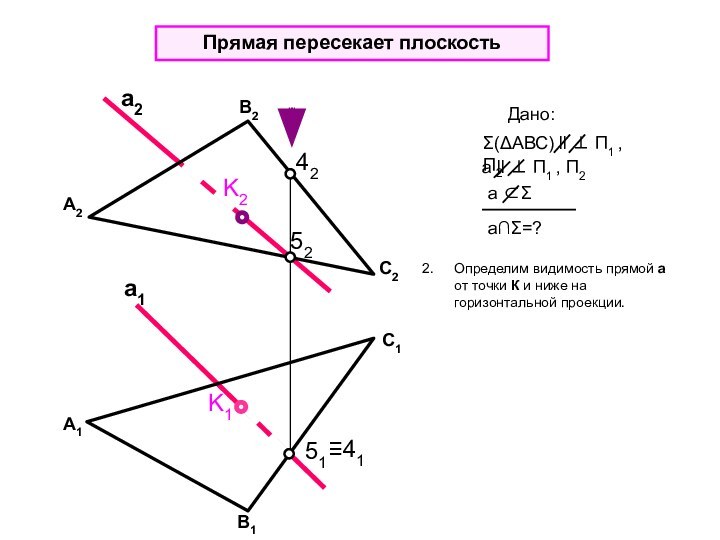
Дано:
aΣ=?
Σ a = K
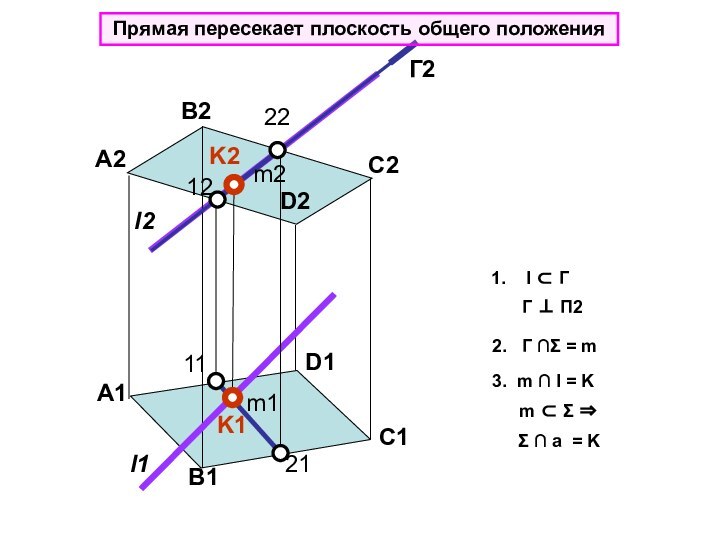
Прямая пересекает плоскость общего положения
m Σ
Σ l = K
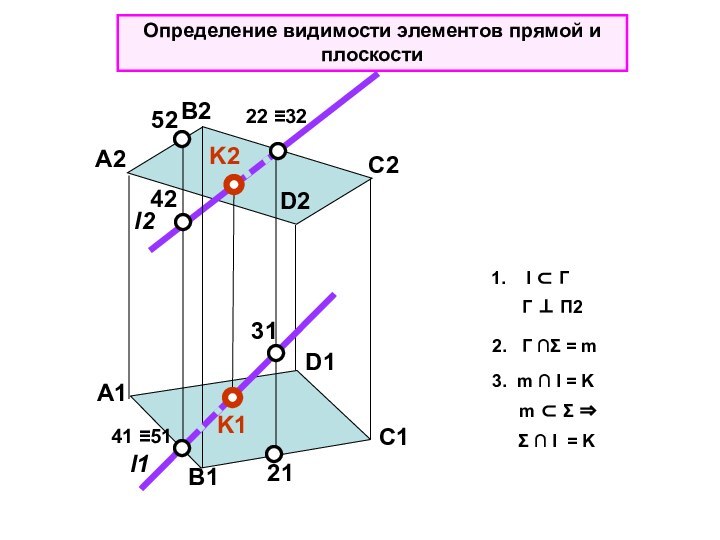
Определение видимости элементов прямой и плоскости
C1
A1
B1
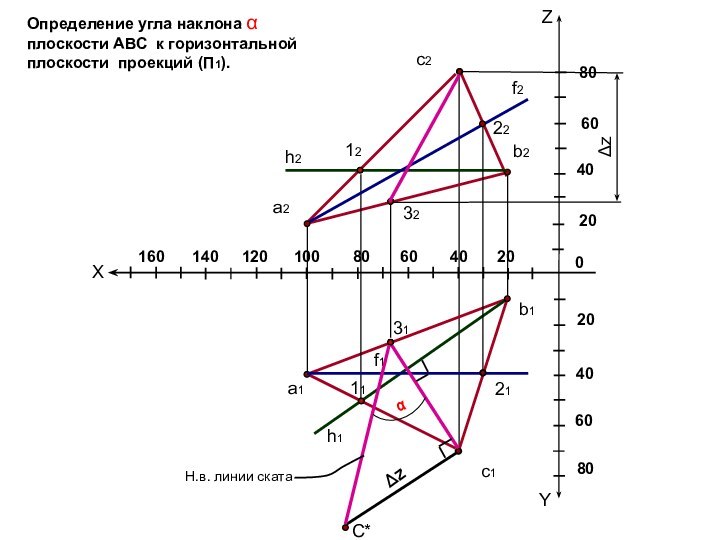
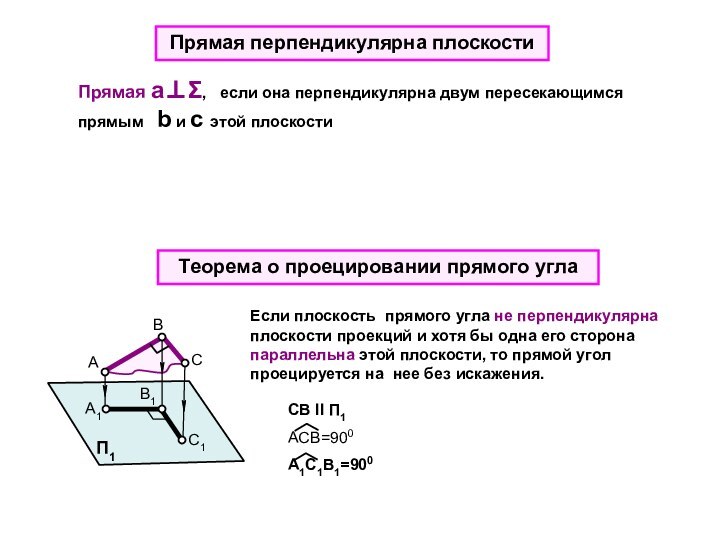
Если плоскость прямого угла не перпендикулярна плоскости проекций и хотя бы одна его сторона параллельна этой плоскости, то прямой угол проецируется на нее без искажения.
CB ll П1
ACB=900
A1C1B1=900
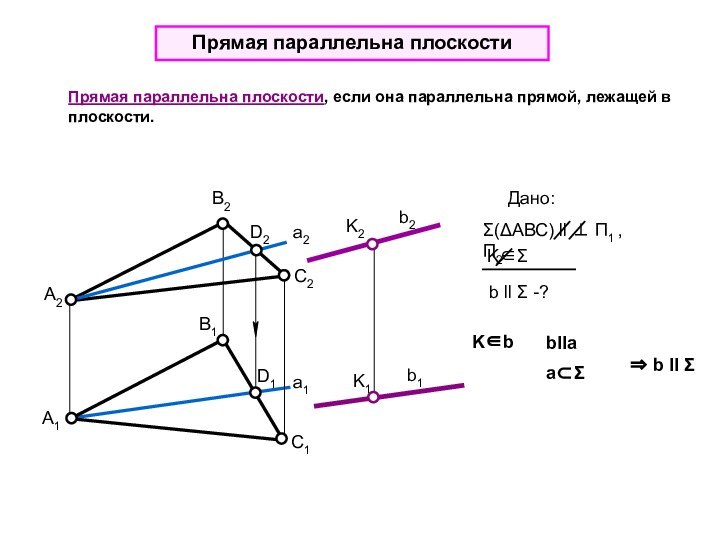
a f f ll П2
h Σ f Σ
aΣ
6. Г1 = [56]
7. Г1 = [78]
8. [56] [78] =N
Σ= MN
Σ [FE] = M
Дано:
Σ= MN -?
4. [DF] Г1
5. Г1 Σ = [34]
6. [34] [DF] = N
[34] Σ
Σ [DF] = N
Σ= MN
N1
N2
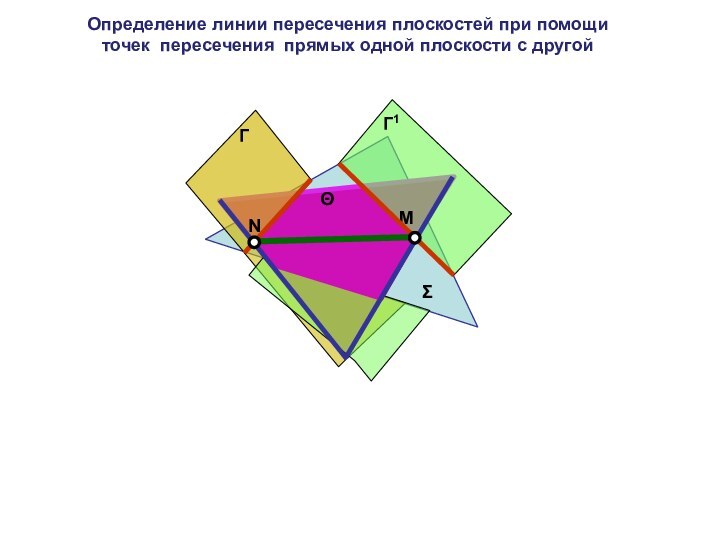
Определение линии пересечения плоскостей при помощи точек пересечения прямых одной плоскости с другой