Презентация на тему Развертки поверхностей

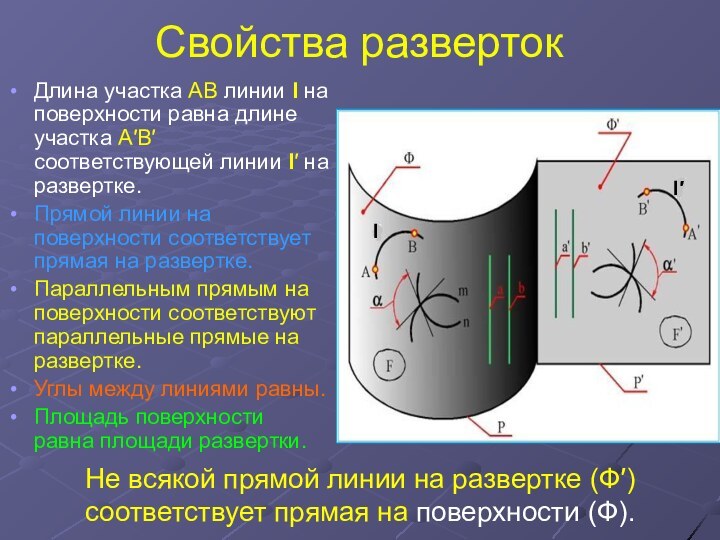
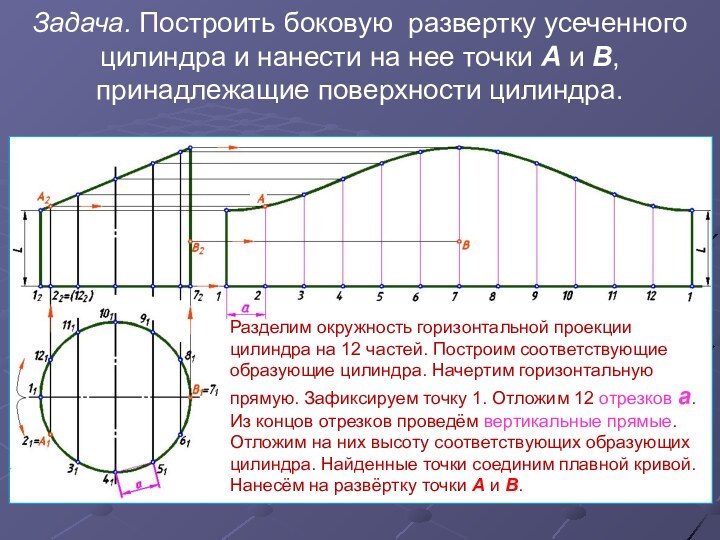
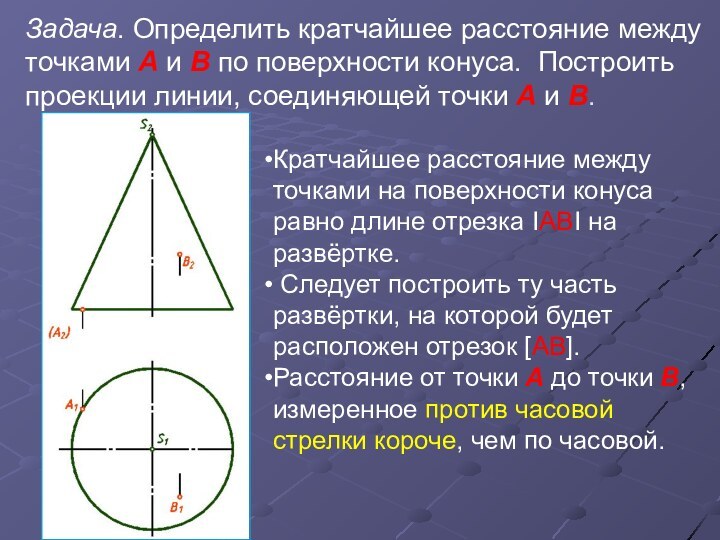
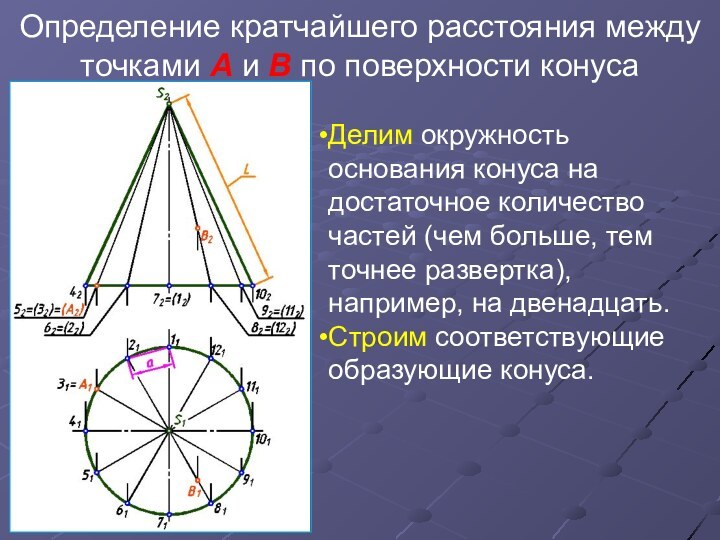
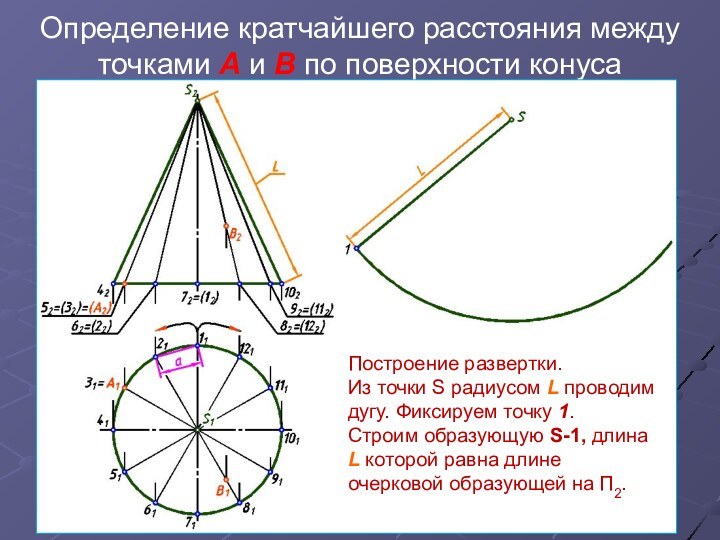
равна длине участка А′B′ соответствующей линии l′ на развертке.
Прямой

линии на поверхности соответствует прямая на развертке.
Параллельным прямым на поверхности соответствуют параллельные прямые на развертке.
Углы между линиями равны.
Площадь поверхности равна площади развертки.

Не всякой прямой линии на развертке (Ф′) соответствует прямая на поверхности (Ф).

ее боковые ребра параллельны плоскости П2 и проецируются на

нее в натуральную величину. Стороны оснований являются горизонталями и проецируются на плоскость П1 без искажения. Длины сторон каждой грани известны. Боковые грани наклонной призмы являются параллелограммами, которые не могут быть построены по четырем сторонам. Для построения параллелограмма необходимо помимо длины сторон знать еще его высоту. Для определения высот граней пересечем призму плоскостью Σ(Σ2), перпендикулярной к ребрам, и определим истинную величину сечения способом замены плоскостей проекций. Стороны этого нормального сечения и будут высотами соответствующих граней.

Задача. Построить развертку наклонной призмы способом нормального сечения.

плоскостью Σ(Σ2), перпендикулярной к ребрам.
Построим горизонтальную проекцию нормального сечения.

способом замены плоскостей проекций.

проводим горизонтальную прямую m и откладываем на ней отрезки

|1–2|=|14–24|, |2–З|=|24–34| и |3–1|=|34–14|.

Через точки 1, 2, 3, 1 проводим перпендикуляры к прямой m и откладываем на них величины боковых ребер так, чтобы |А1|=|А212| и |1К|=|12К2|, |В2|=|В222| и |2L| = |22L2| и т.д.

Соединив концы построенных отрезков, получим развертку боковой поверхности призмы.

поверхности призмы оба основания, получим полную развертку призмы.

на нее точки А и В, принадлежащие поверхности цилиндра.
Разделим

окружность горизонтальной проекции цилиндра на 12 частей. Построим соответствующие образующие цилиндра. Начертим горизонтальную прямую. Зафиксируем точку 1. Отложим 12 отрезков а.
Из концов отрезков проведём вертикальные прямые. Отложим на них высоту соответствующих образующих цилиндра. Найденные точки соединим плавной кривой. Нанесём на развёртку точки А и В.

В по поверхности конуса. Построить проекции линии, соединяющей точки

А и В.

Кратчайшее расстояние между точками на поверхности конуса равно длине отрезка IABI на развёртке.
Следует построить ту часть развёртки, на которой будет расположен отрезок [AB].
Расстояние от точки А до точки В, измеренное против часовой стрелки короче, чем по часовой.

по поверхности конуса
Делим окружность основания конуса на достаточное количество

частей (чем больше, тем точнее развертка), например, на двенадцать.
Строим соответствующие образующие конуса.

по поверхности конуса
Построение развертки.
Из точки S радиусом L проводим

дугу. Фиксируем точку 1.
Строим образующую S-1, длина L которой равна длине очерковой образующей на П2.

по поверхности конуса
Откладываем на дуге длину хорды IаI восемь

раз. Строим образующие конуса S-2, S-3, S-4… на развёртке.
Наносим точку А.

по поверхности конуса
Определим расстояние ISBI построив точку В′ на

крайней образующей конуса. На восьмой образующей конуса на развёртке делаем засечку радиусом ISBI.
Наносим точку В.

по поверхности конуса
Соединив точки А и В получим отрезок

IАBI - кратчайшее расстояние между точками А и В по поверхности конуса. Для построения проекций этого отрезка определим точки пересечения образующих конуса с отрезком [АB] на развёртке.

по поверхности конуса
Замеряем расстояние от точки S до точки

пересечения, например, R7. Этим радиусом делаем засечку на крайней образующей конуса. Из этой точки проводим отрезок, параллельный основанию до пересечения с 7-ой образующей и т. д. Полученные точки соединим плавной кривой.