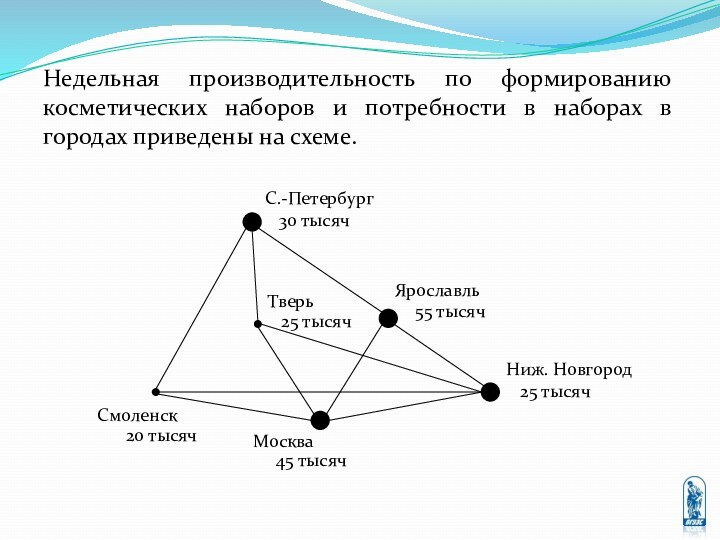
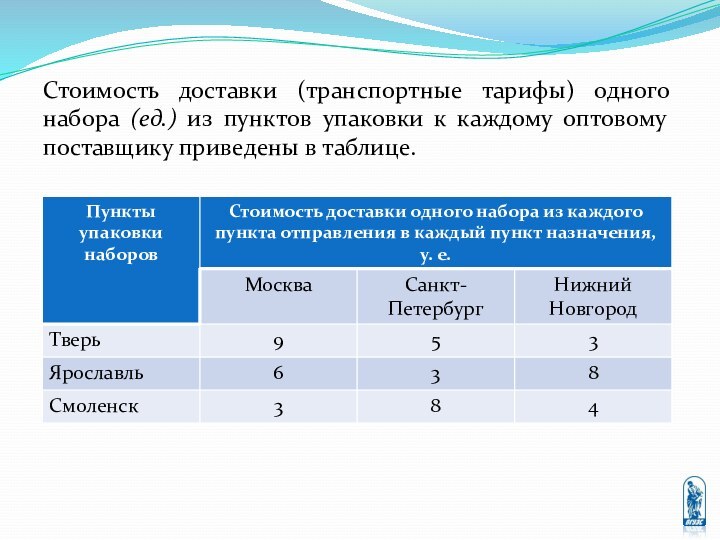
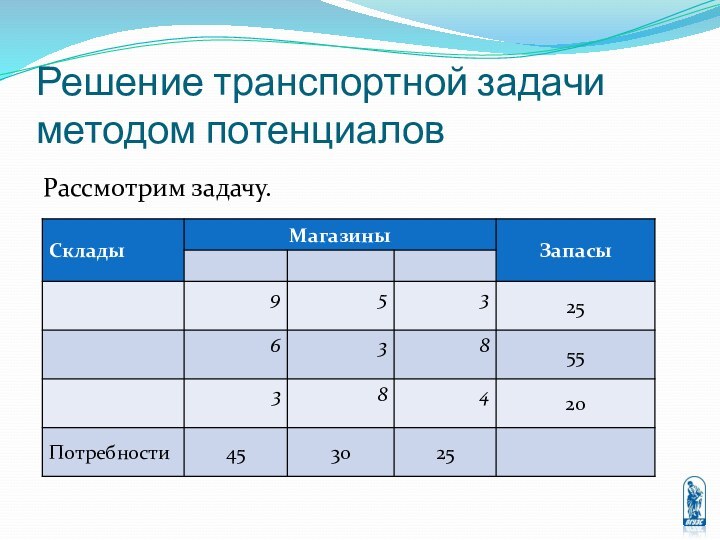
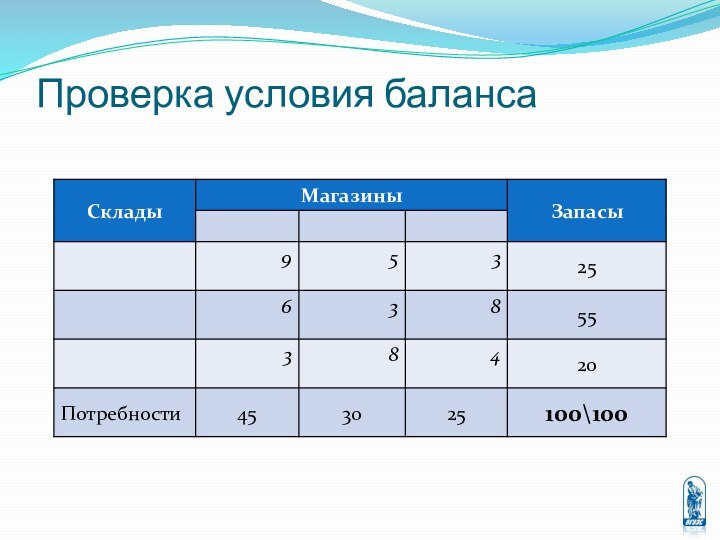
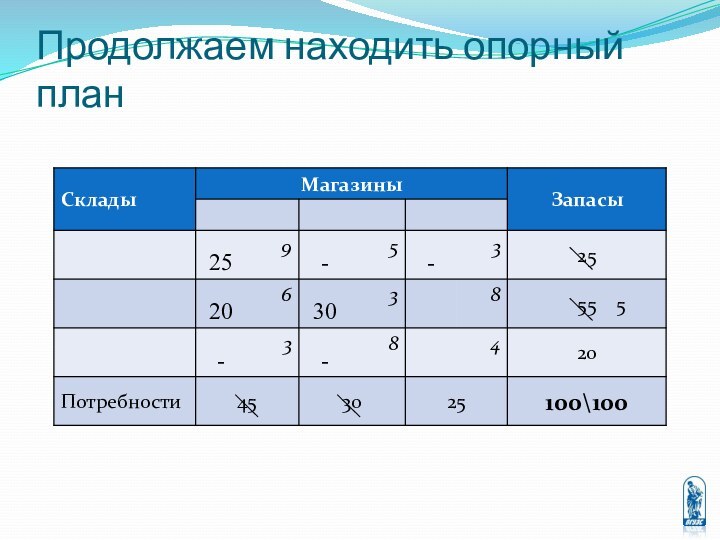
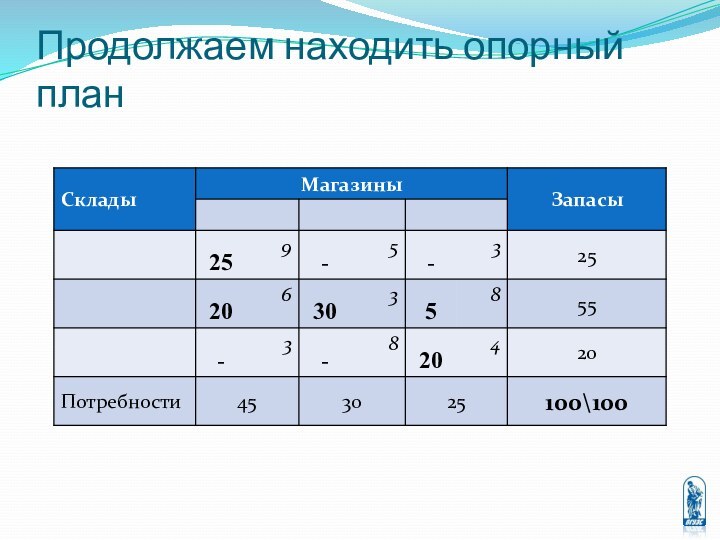
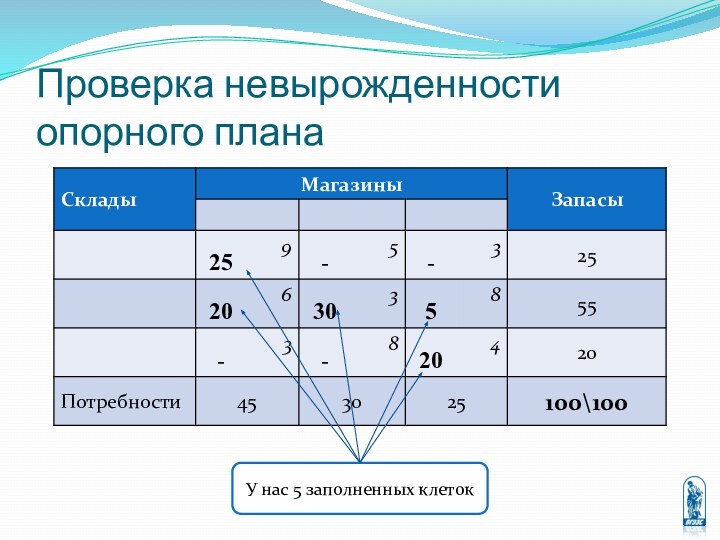
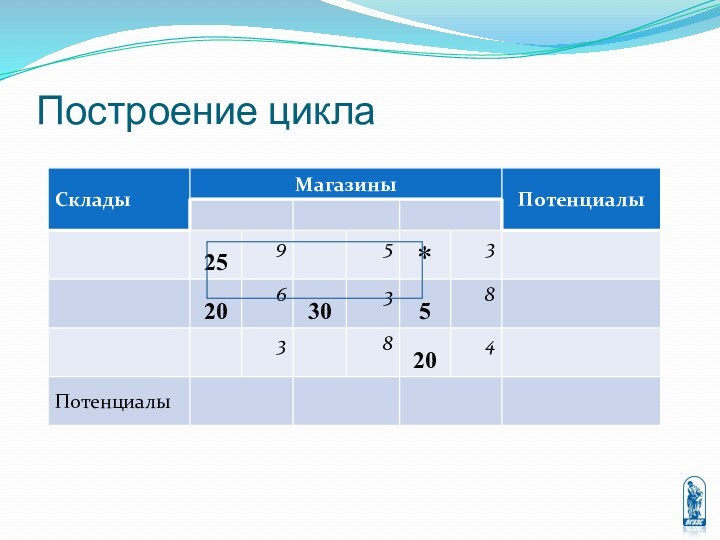
перевозке некоторых однородных грузов из пунктов отправления в пункты
назначения, причём известны стоимости перевозки единицы груза между любыми двумя пунктами отправления и назначения.Требуется составить оптимальный план перевозок, то есть определить количество груза перевозимого из каждого пункта отправления в каждый пункт назначения, при котором суммарная стоимость всех перевозок будет минимальной.