- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Взаимно перпендикулярные прямые и плоскости
Содержание
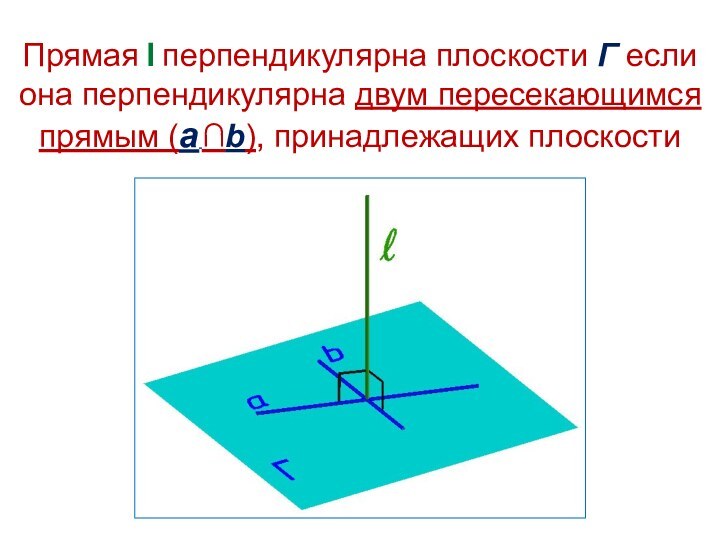
- 2. Прямая l перпендикулярна плоскости Г если она перпендикулярна двум пересекающимся прямым (а ∩b), принадлежащих плоскости
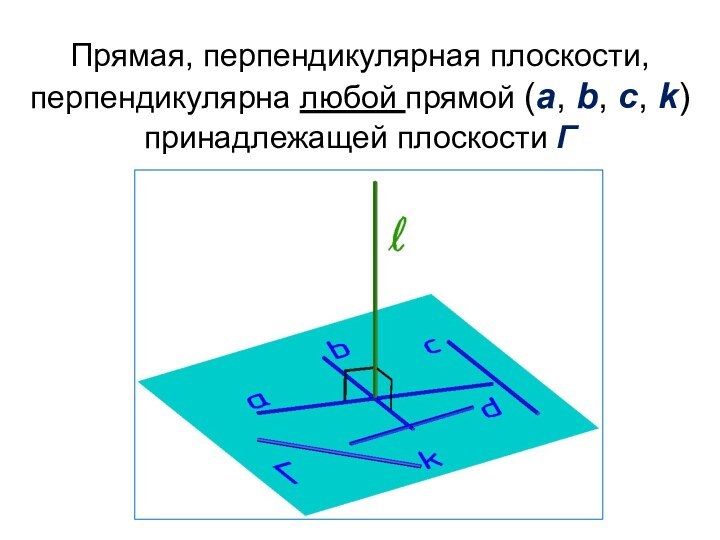
- 3. Прямая, перпендикулярная плоскости, перпендикулярна любой прямой (а, b, c, k) принадлежащей плоскости Г
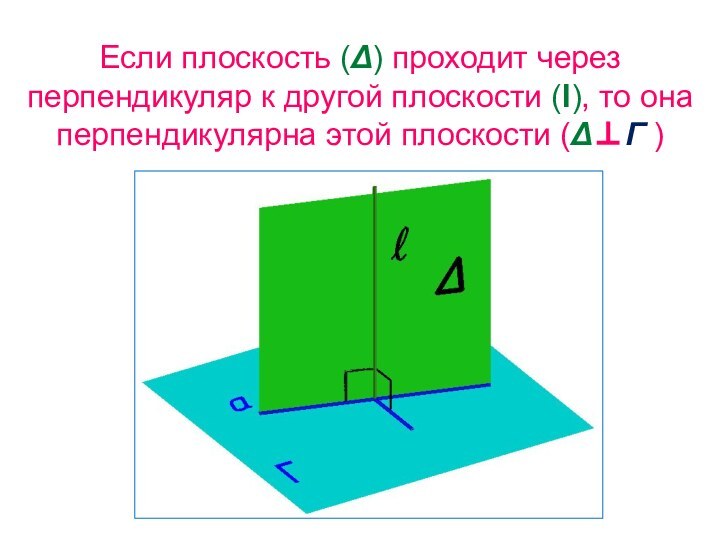
- 4. Если плоскость (Δ) проходит через перпендикуляр к
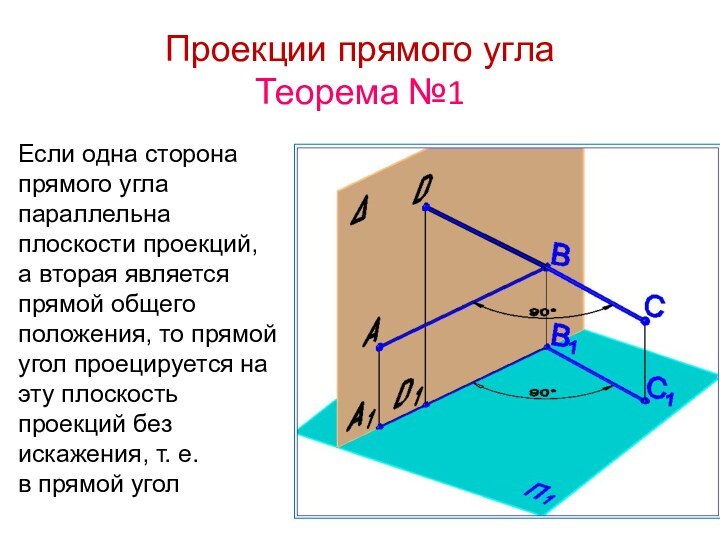
- 5. Проекции прямого угла Теорема №1Если одна сторона
- 6. Прямая, перпендикулярная к плоскости общего положения. Теорема
- 7. Основные задачиЗадача. Опустить перпендикуляр l(l1 l2) из точки А на плоскость общего положения Σ(а∩b).
- 8. Опустить перпендикуляр l(l1 l2) из точки А
- 9. Опустить перпендикуляр l(l1 l2) из точки А
- 10. Опустить перпендикуляр l(l1 l2) из точки А
- 11. Опустить перпендикуляр l(l1 l2) из точки А
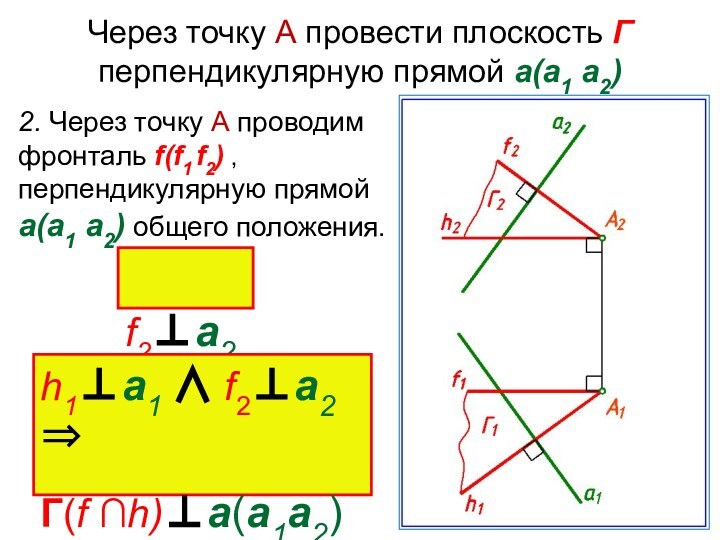
- 12. Основные задачиЗадача. Через точку А провести плоскость Г перпендикулярную прямой а(а1 а2) общего положения.
- 13. Через точку А провести плоскость Г перпендикулярную
- 14. Через точку А провести плоскость Г перпендикулярную
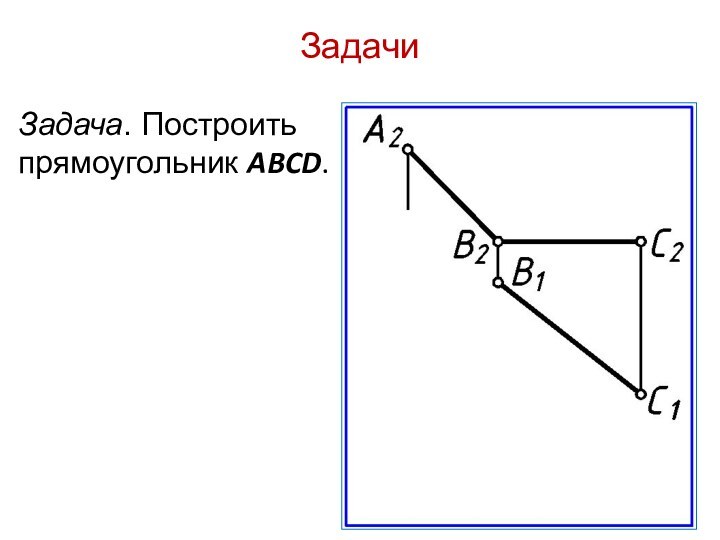
- 15. ЗадачиЗадача. Построить прямоугольник ABCD.
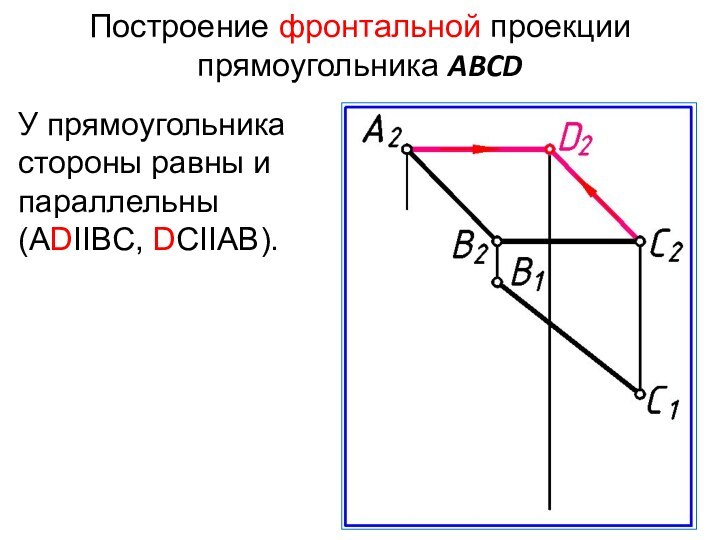
- 16. Построение фронтальной проекции прямоугольника ABCDУ прямоугольника стороны равны и параллельны (ADIIBC, DCIIAB).
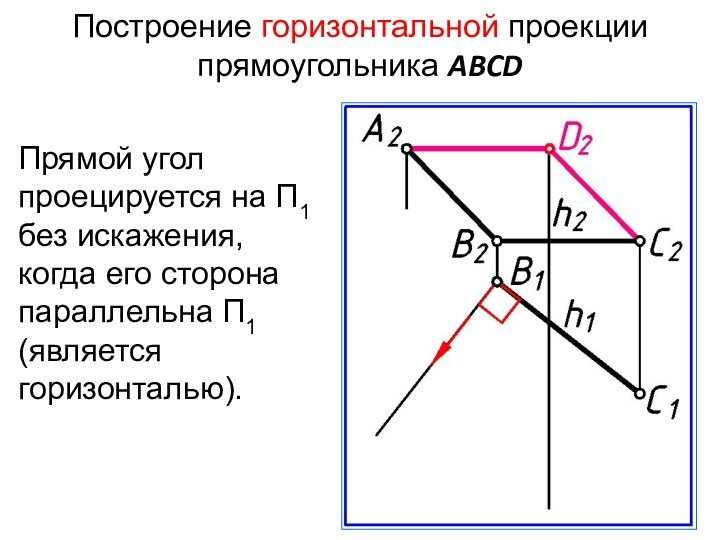
- 17. Построение горизонтальной проекции прямоугольника ABCDПрямой угол проецируется
- 18. Построение горизонтальной проекции прямоугольника ABCDПо линии связи по принадлежности находим горизонтальную проекцию А1 вершины А.
- 19. Построение горизонтальной проекции прямоугольника ABCDУ параллельных прямых
- 20. Прямоугольник ABCD
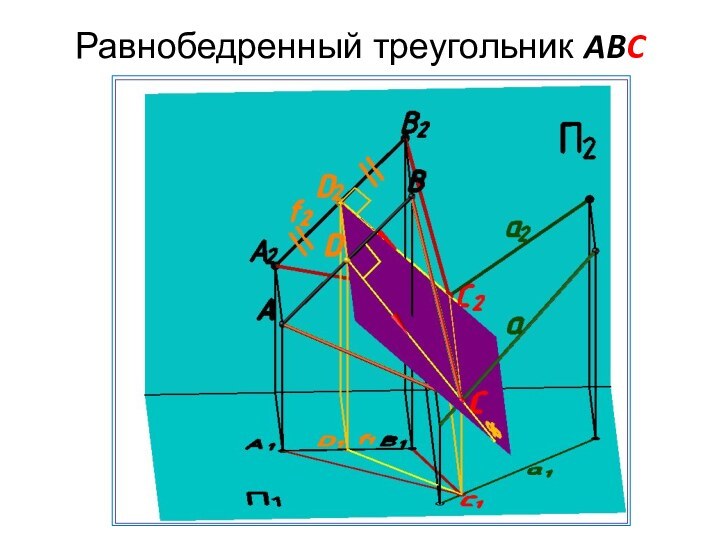
- 21. ЗадачиЗадача. Построить равнобедренный треугольник ABC с основанием AB и вершиной С на прямой а.
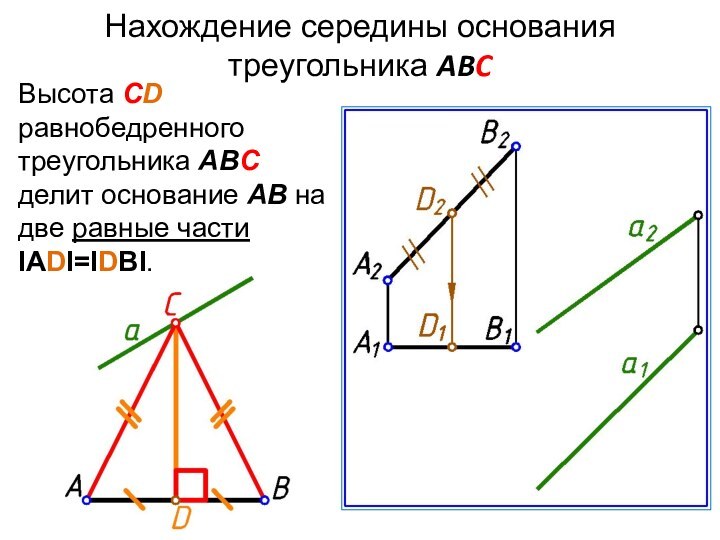
- 22. Нахождение середины основания треугольника ABCВысота СD равнобедренного
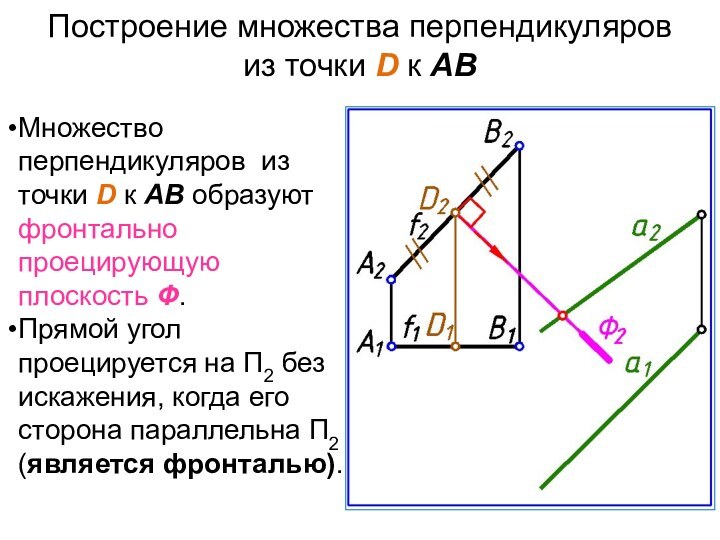
- 23. Построение множества перпендикуляров из точки D к
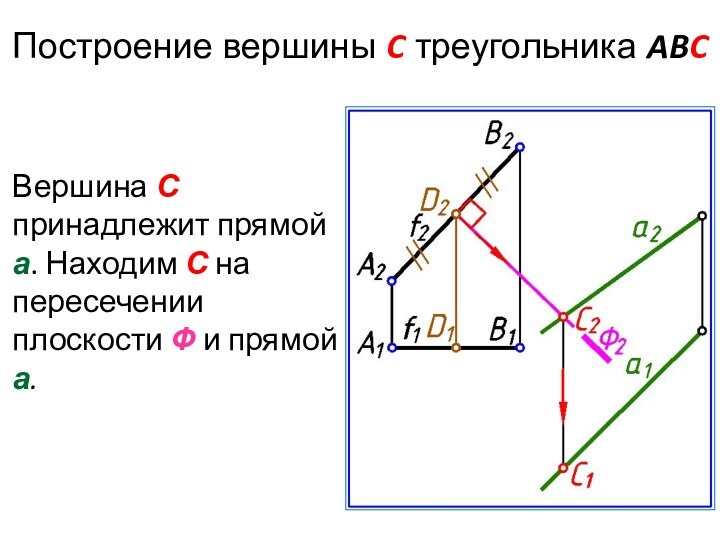
- 24. Построение вершины C треугольника ABCВершина С принадлежит
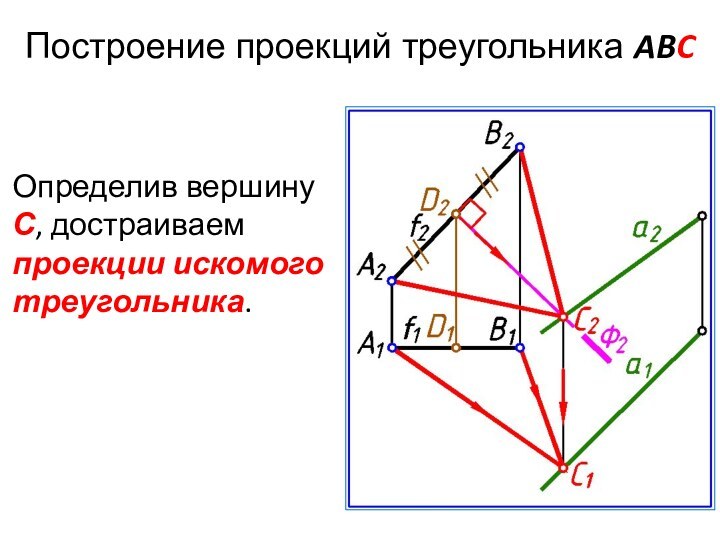
- 25. Построение проекций треугольника ABCОпределив вершину С, достраиваем проекции искомого треугольника.
- 26. Равнобедренный треугольник ABC
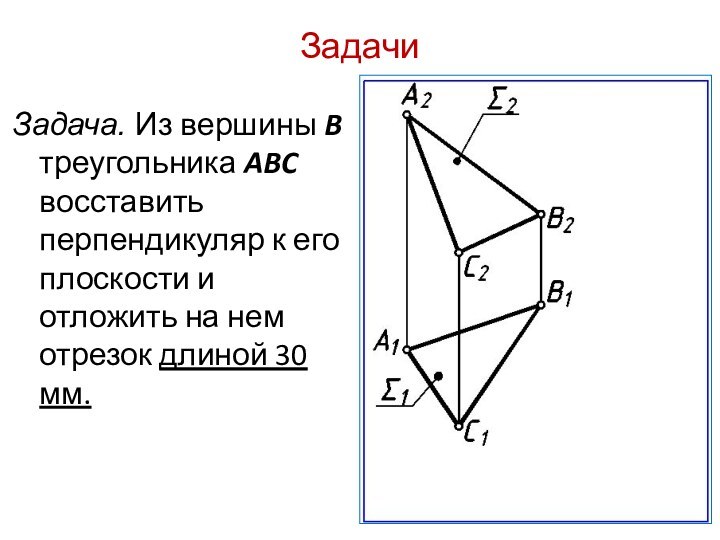
- 27. ЗадачиЗадача. Из вершины B треугольника ABC восставить
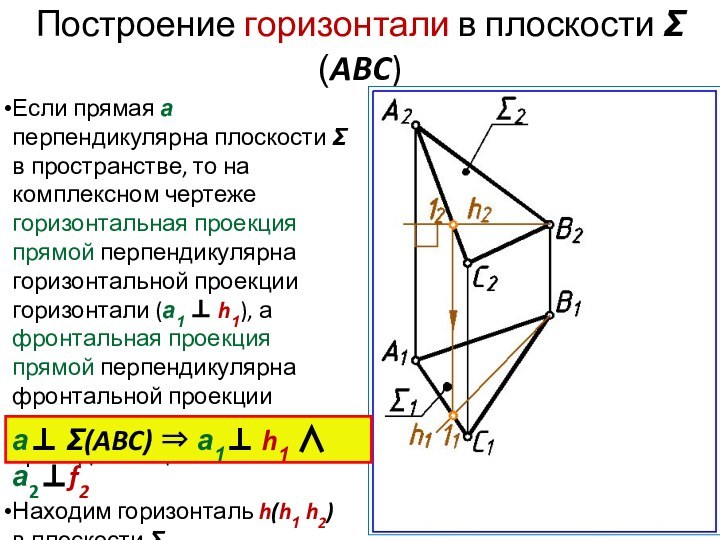
- 28. Построение горизонтали в плоскости Σ(ABC)Если прямая а
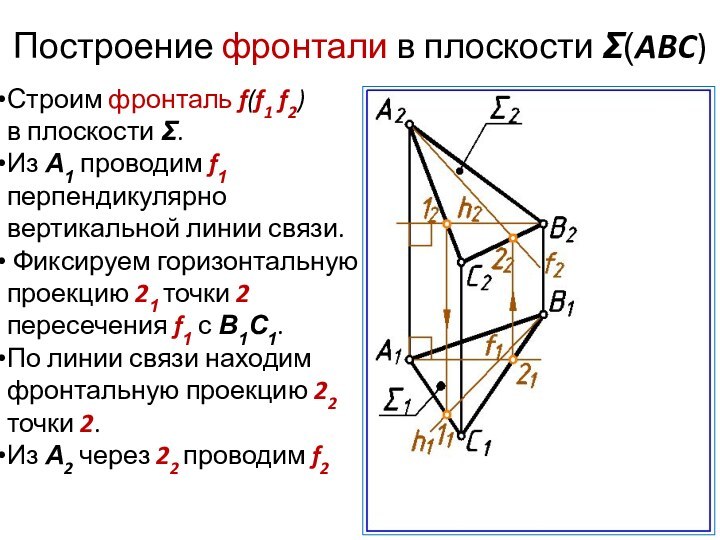
- 29. Построение фронтали в плоскости Σ(ABC)Строим фронталь f(f1
- 30. Построение фронтальной проекции (a2) перпендикуляра а Строим
- 31. Построение горизонтальной проекции (a1) перпендикуляра аСтроим горизонтальную
- 32. Отрезок длиной 30 мм на перпендикуляре а(a1a2)На
- 33. Отрезок длиной 30 мм на перпендикуляре а(a1a2)Для
- 34. Отрезок длиной 30 мм на перпендикуляре а(a1a2)На
- 35. Отрезок [BЕ] перпендикуляра а(a1a2) длиной 30 мм
- 36. ЗадачиЗадача. Построить множество точек, равноудаленных от концов
- 37. Множество точек, равноудаленных от концов отрезка [АВ]Делим AB на две равные части: IАСI=IВСI.
- 38. Множество точек, равноудаленных от концов отрезка [АВ]Прямой
- 39. Множество точек, равноудаленных от концов отрезка [АВ]
- 40. Множество точек, равноудаленных от концов отрезка [АВ] есть плоскость Σ(h ∩ f) АВ
- 41. ЗадачиЗадача. Через прямую а(а1 а2) провести плоскость
- 42. Построение горизонтальной проекции перпендикуляра к плоскости Г(ABC)Находим
- 43. Построение фронтальной проекции перпендикуляра к плоскости Г(ABC)Находим
- 44. Плоскость Σ перпендикулярная плоскости Г(ABC) общего положенияПлоскость
- 45. Скачать презентацию
- 46. Похожие презентации
Прямая l перпендикулярна плоскости Г если она перпендикулярна двум пересекающимся прямым (а ∩b), принадлежащих плоскости

![Взаимно перпендикулярные прямые и плоскости Отрезок длиной 30 мм на перпендикуляре а(a1a2)На натуральной величине IDBI отрезка [DB]](/img/tmb/13/1231679/e110a8a06c1f634c56171a83ded70b06-720x.jpg)
![Взаимно перпендикулярные прямые и плоскости Отрезок [BЕ] перпендикуляра а(a1a2) длиной 30 мм](/img/tmb/13/1231679/1b412e9827dc00b5d9ea49106f1f5eec-720x.jpg)
![Взаимно перпендикулярные прямые и плоскости ЗадачиЗадача. Построить множество точек, равноудаленных от концов отрезка [АВ]. Записать анализ.Множество точек](/img/tmb/13/1231679/53c8ec2efddf61c8baa16a14c248777d-720x.jpg)
![Взаимно перпендикулярные прямые и плоскости Множество точек, равноудаленных от концов отрезка [АВ]Делим AB на две равные части: IАСI=IВСI.](/img/tmb/13/1231679/826a31cb5cba6389234a661ac8bd7c4a-720x.jpg)
![Взаимно перпендикулярные прямые и плоскости Множество точек, равноудаленных от концов отрезка [АВ]Прямой угол проецируется на П1 без](/img/tmb/13/1231679/b081dfd9d6eb1464b5f4458e91637cc3-720x.jpg)
![Взаимно перпендикулярные прямые и плоскости Множество точек, равноудаленных от концов отрезка [АВ] есть плоскость Σ(h ∩ f)](/img/tmb/13/1231679/1c85a93f6be9e650ca2bb8fd78c4caf0-720x.jpg)
![Взаимно перпендикулярные прямые и плоскости Множество точек, равноудаленных от концов отрезка [АВ] есть плоскость Σ(h ∩ f) АВ](/img/tmb/13/1231679/a1b47d4e07625ab26dcadf7b3a4b11f7-720x.jpg)
Слайд 2 Прямая l перпендикулярна плоскости Г если она перпендикулярна
двум пересекающимся прямым (а ∩b), принадлежащих плоскости
Слайд 3 Прямая, перпендикулярная плоскости, перпендикулярна любой прямой (а, b,
c, k) принадлежащей плоскости Г
Слайд 4 Если плоскость (Δ) проходит через перпендикуляр к другой
плоскости (l), то она перпендикулярна этой плоскости (ΔГ )
Слайд 5
Проекции прямого угла
Теорема №1
Если одна сторона прямого угла
параллельна плоскости проекций, а вторая является прямой общего положения, то
прямой угол проецируется на эту плоскость проекций без искажения, т. е. в прямой угол
Слайд 6
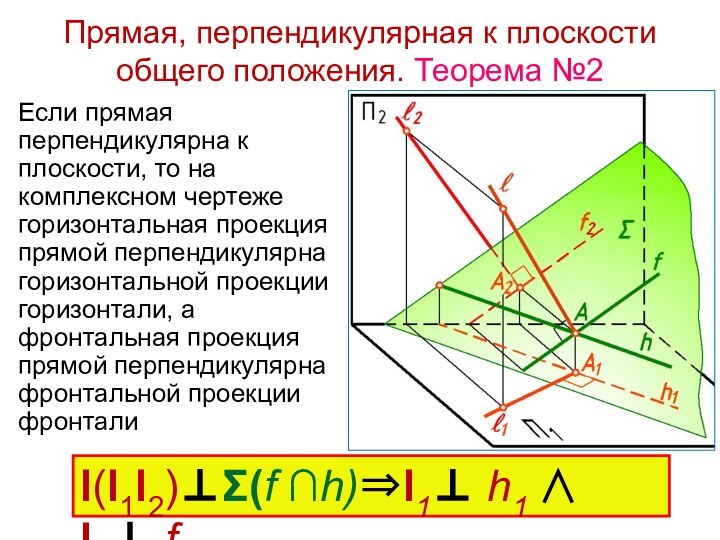
Прямая, перпендикулярная к плоскости общего положения. Теорема №2
l(l1l2)Σ(f
∩h)l1 h1 l2 f2
Если прямая перпендикулярна к плоскости,
то на комплексном чертеже горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали
Слайд 7
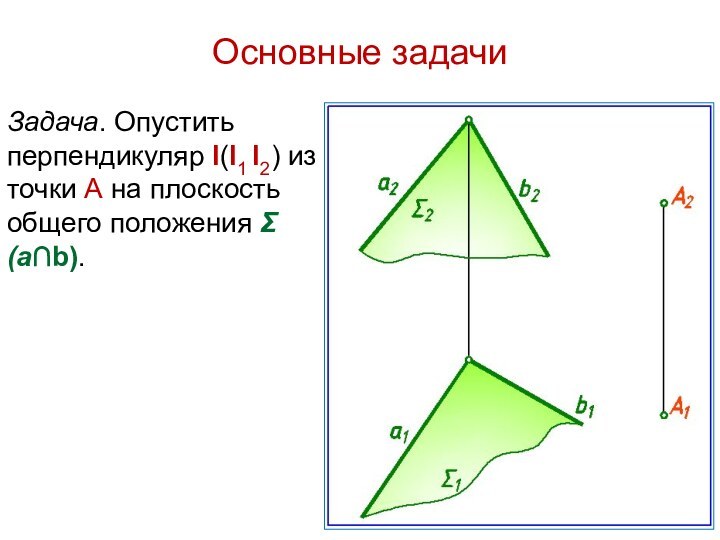
Основные задачи
Задача. Опустить перпендикуляр l(l1 l2) из точки
А на плоскость общего положения Σ(а∩b).
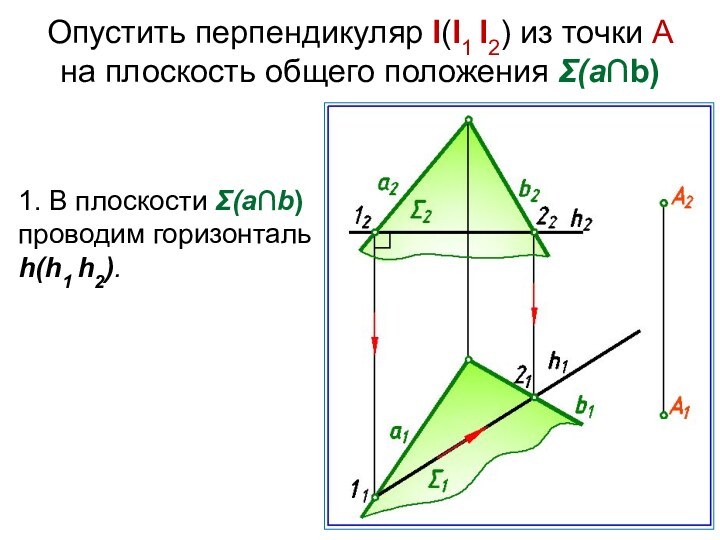
Слайд 8 Опустить перпендикуляр l(l1 l2) из точки А на плоскость
общего положения Σ(а∩b)
1. В плоскости Σ(а∩b) проводим горизонталь
h(h1 h2).
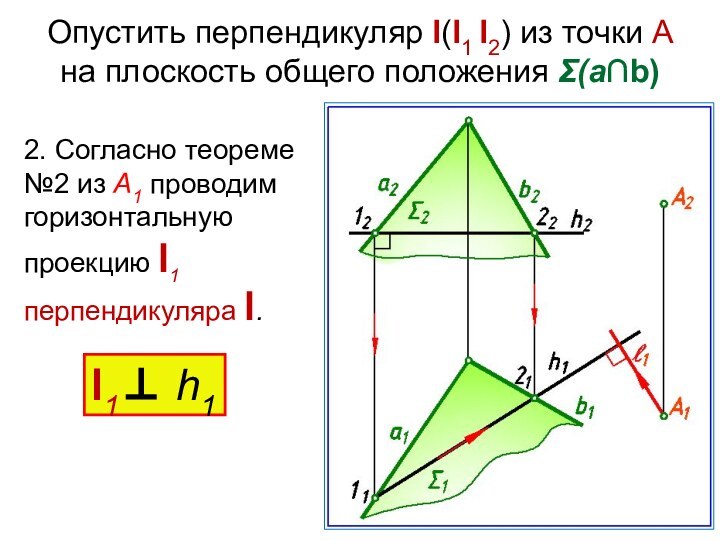
Слайд 9 Опустить перпендикуляр l(l1 l2) из точки А на плоскость
общего положения Σ(а∩b)
2. Согласно теореме №2 из А1 проводим
горизонтальную проекцию l1 перпендикуляра l.l1 h1
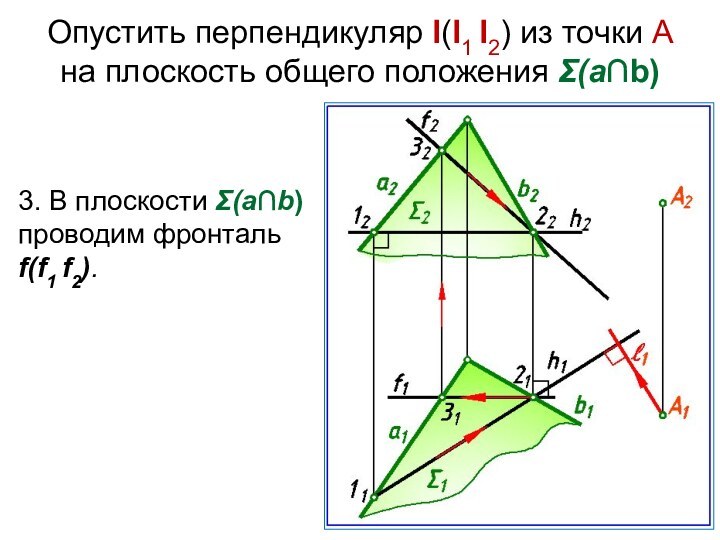
Слайд 10 Опустить перпендикуляр l(l1 l2) из точки А на плоскость
общего положения Σ(а∩b)
3. В плоскости Σ(а∩b) проводим фронталь
f(f1 f2).
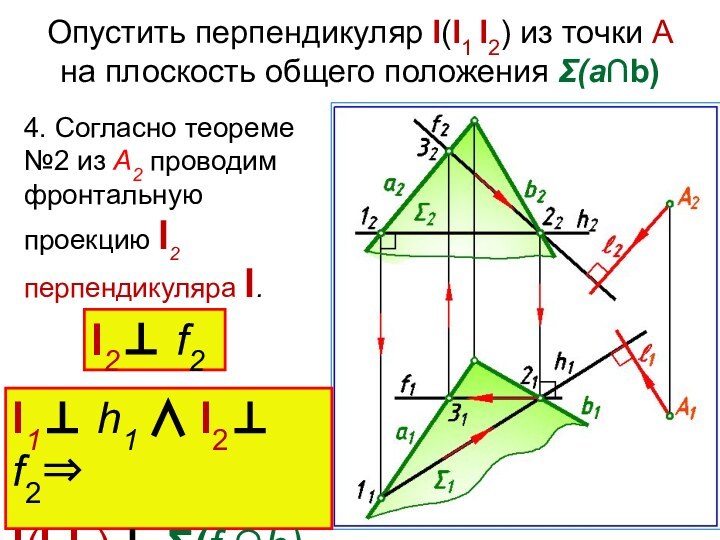
Слайд 11 Опустить перпендикуляр l(l1 l2) из точки А на плоскость
общего положения Σ(а∩b)
4. Согласно теореме №2 из А2 проводим
фронтальную проекцию l2 перпендикуляра l.l2 f2
l1 h1 l2 f2
l(l1l2) Σ(f ∩h)
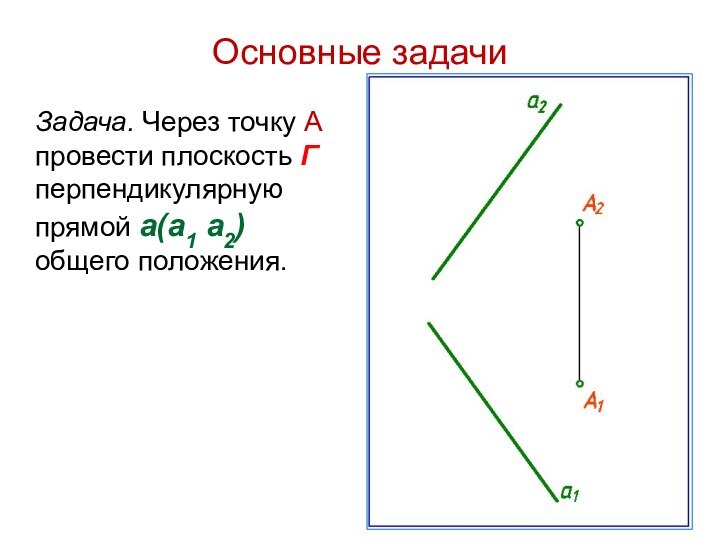
Слайд 12
Основные задачи
Задача. Через точку А провести плоскость Г
перпендикулярную прямой а(а1 а2) общего положения.
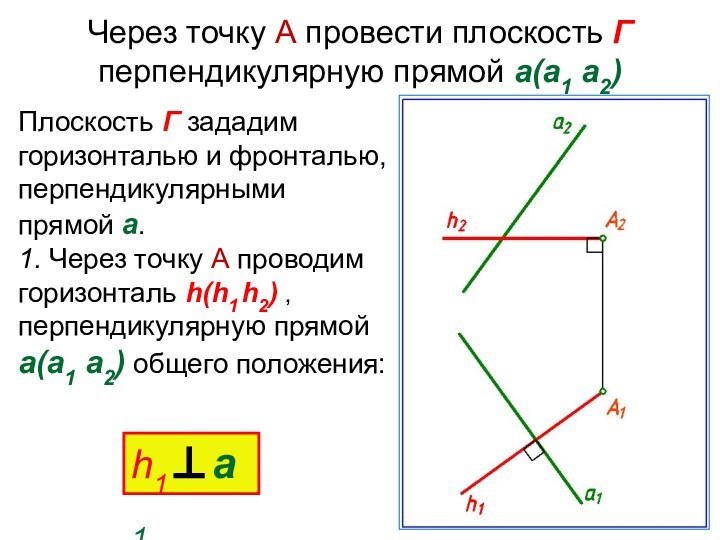
Слайд 13 Через точку А провести плоскость Г перпендикулярную прямой
а(а1 а2)
Плоскость Г зададим горизонталью и фронталью, перпендикулярными прямой
а. 1. Через точку А проводим горизонталь h(h1 h2) , перпендикулярную прямой а(а1 а2) общего положения:
h1а1
Слайд 14 Через точку А провести плоскость Г перпендикулярную прямой
а(а1 а2)
2. Через точку А проводим фронталь f(f1 f2)
, перпендикулярную прямой а(а1 а2) общего положения. f2а2
h1а1 f2а2
Г(f ∩h)а(а1а2)
Слайд 16
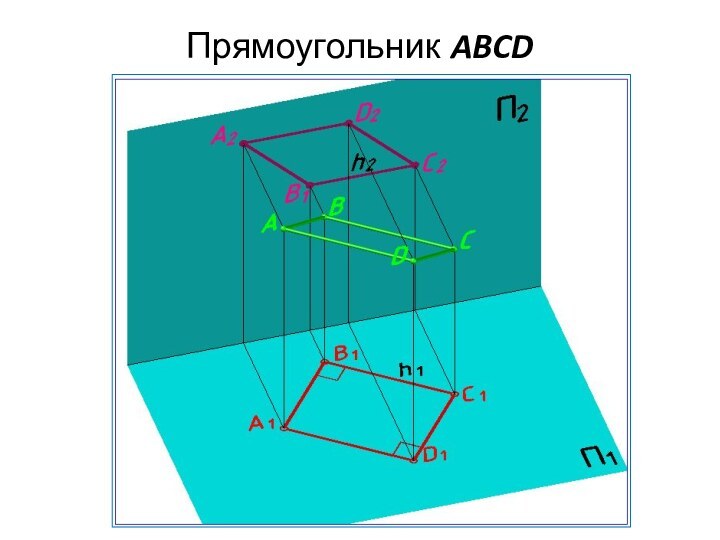
Построение фронтальной проекции прямоугольника ABCD
У прямоугольника стороны равны
и параллельны (ADIIBC, DCIIAB).
Слайд 17
Построение горизонтальной проекции прямоугольника ABCD
Прямой угол проецируется на
П1 без искажения, когда его сторона параллельна П1 (является
горизонталью).
Слайд 18
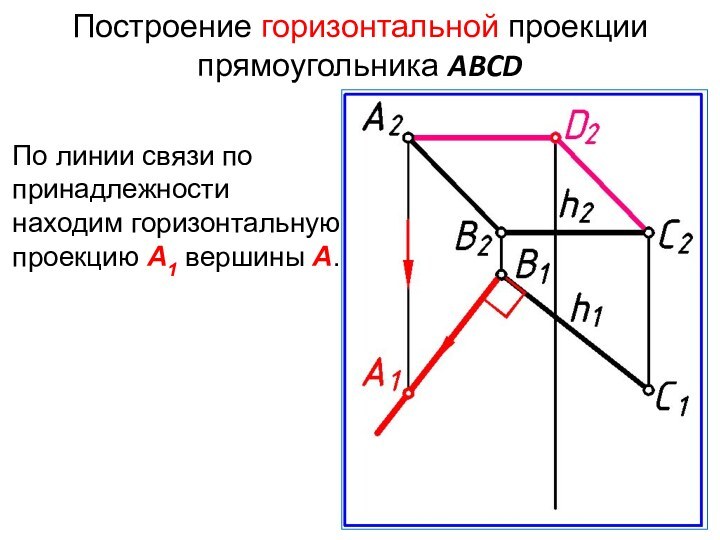
Построение горизонтальной проекции прямоугольника ABCD
По линии связи по
принадлежности находим горизонтальную проекцию А1 вершины А.
Слайд 19
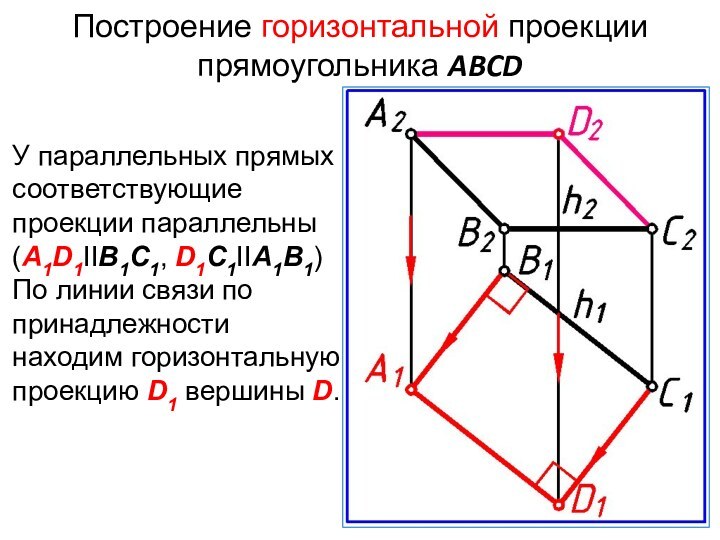
Построение горизонтальной проекции прямоугольника ABCD
У параллельных прямых соответствующие
проекции параллельны (A1D1IIB1C1, D1C1IIA1B1)
По линии связи по принадлежности находим
горизонтальную проекцию D1 вершины D.
Слайд 21
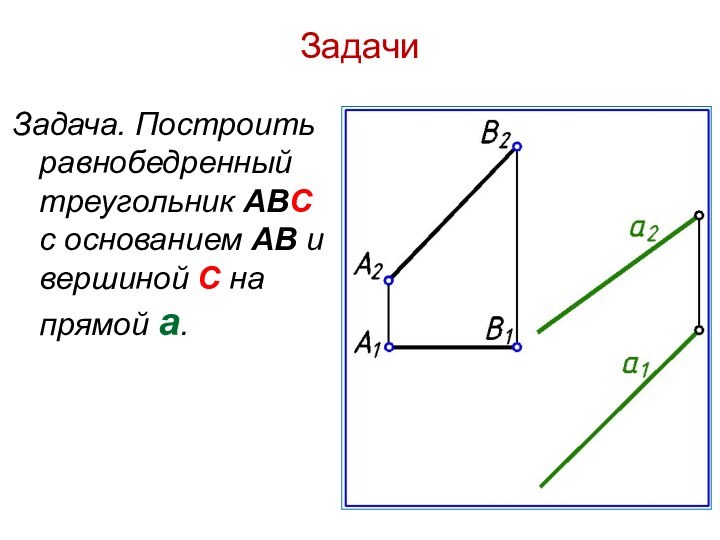
Задачи
Задача. Построить равнобедренный треугольник ABC с основанием AB
и вершиной С на прямой а.
Слайд 22
Нахождение середины основания треугольника ABC
Высота СD равнобедренного треугольника
ABC делит основание AB на две равные части IADI=IDBI.
Слайд 23
Построение множества перпендикуляров
из точки D к АВ
Множество
перпендикуляров из точки D к АВ образуют фронтально проецирующую
плоскость Ф.Прямой угол проецируется на П2 без искажения, когда его сторона параллельна П2 (является фронталью).
Слайд 24
Построение вершины C треугольника ABC
Вершина С принадлежит прямой
а. Находим С на пересечении плоскости Ф и прямой
а.
Слайд 25
Построение проекций треугольника ABC
Определив вершину С, достраиваем проекции
искомого треугольника.
Слайд 27
Задачи
Задача. Из вершины B треугольника ABC восставить перпендикуляр
к его плоскости и отложить на нем отрезок длиной
30 мм.
Слайд 28
Построение горизонтали в плоскости Σ(ABC)
Если прямая а перпендикулярна
плоскости Σ в пространстве, то на комплексном чертеже горизонтальная
проекция прямой перпендикулярна горизонтальной проекции горизонтали (а1 h1), а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (а2 f2), принадлежащих плоскости Σ.Находим горизонталь h(h1 h2) в плоскости Σ.
а Σ(ABC) а1 h1 а2f2
Слайд 29
Построение фронтали в плоскости Σ(ABC)
Строим фронталь f(f1 f2)
в
плоскости Σ.
Из А1 проводим f1 перпендикулярно вертикальной линии связи.
Фиксируем горизонтальную проекцию 21 точки 2 пересечения f1 с В1С1.По линии связи находим фронтальную проекцию 22 точки 2.
Из А2 через 22 проводим f2
Слайд 30
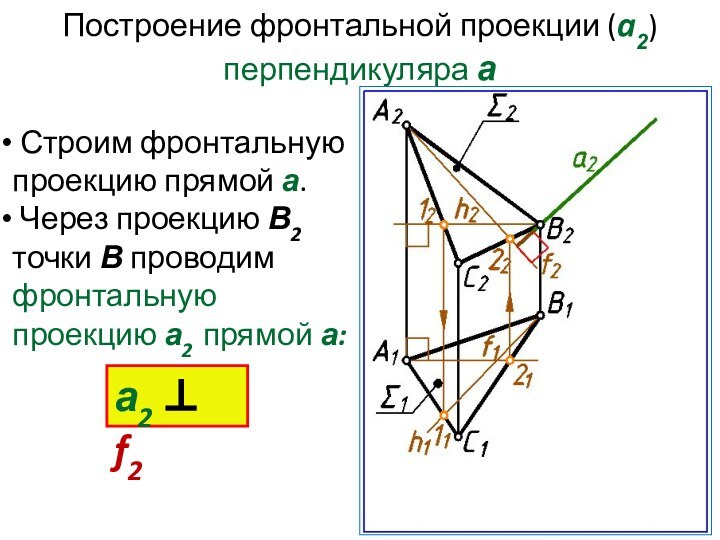
Построение фронтальной проекции (a2) перпендикуляра а
Строим фронтальную
проекцию прямой а.
Через проекцию В2 точки В проводим
фронтальную проекцию а2 прямой а:а2 f2
Слайд 31
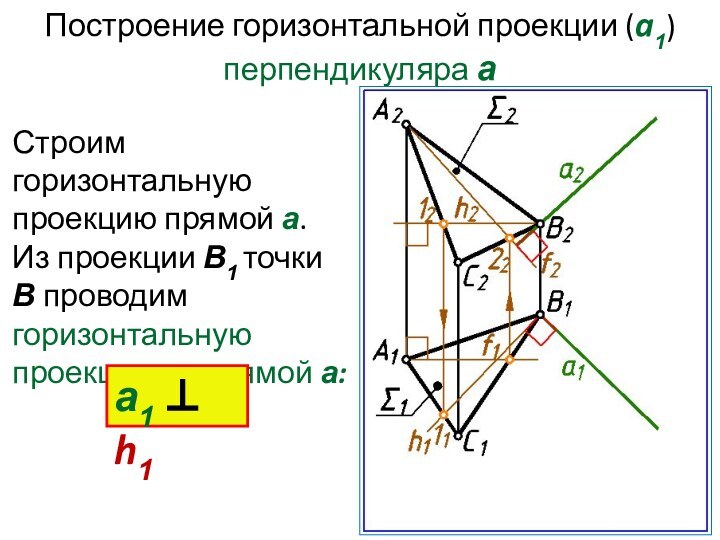
Построение горизонтальной проекции (a1) перпендикуляра а
Строим горизонтальную проекцию
прямой а.
Из проекции В1 точки В проводим горизонтальную проекцию
а1 прямой а:а1 h1
Слайд 32
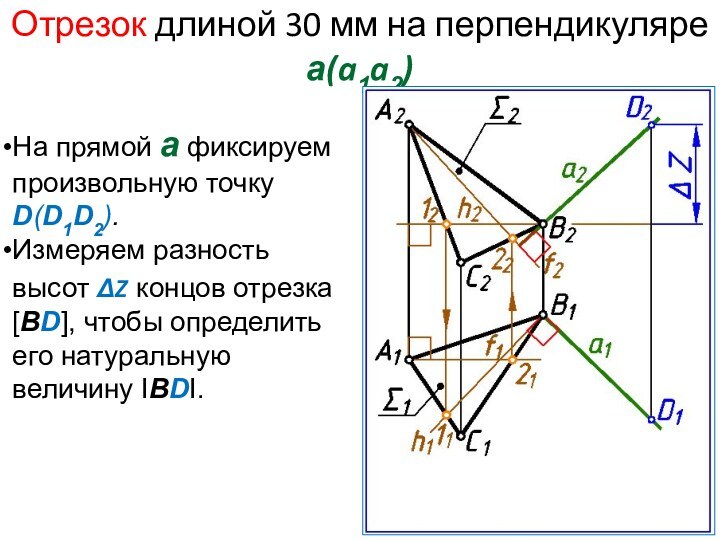
Отрезок длиной 30 мм на перпендикуляре а(a1a2)
На прямой
а фиксируем произвольную точку D(D1D2).
Измеряем разность высот ΔZ концов
отрезка [BD], чтобы определить его натуральную величину IBDI.
Слайд 33
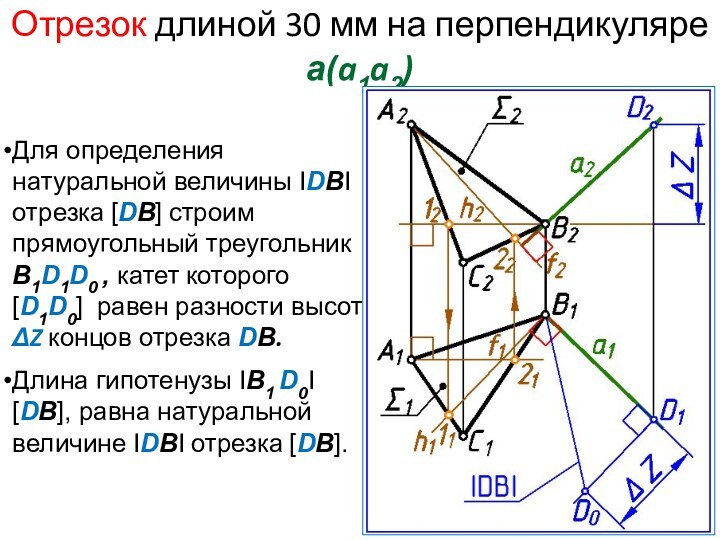
Отрезок длиной 30 мм на перпендикуляре а(a1a2)
Для определения
натуральной величины IDBI отрезка [DB] строим прямоугольный треугольник B1D1D0
, катет которого [D1D0] равен разности высот ΔZ концов отрезка DB.Длина гипотенузы IB1 D0I [DB], равна натуральной величине IDBI отрезка [DB].
Слайд 34
Отрезок длиной 30 мм на перпендикуляре а(a1a2)
На натуральной
величине IDBI отрезка [DB] находим точку Е(Е1Е2), отстоящую от
B на 30 мм.Отрезок [BЕ] искомый.
Слайд 36
Задачи
Задача. Построить множество точек, равноудаленных от концов отрезка
[АВ]. Записать анализ.
Множество точек пространства, равноудаленных от двух данных
точек, есть плоскость, проходящая через середину отрезка [АВ], и перпендикулярная
отрезку [AB] :IАСI=IВСI, С Σ(h ∩f) АВ,
h1 А1В1 f2 А2В2.
Слайд 37
Множество точек, равноудаленных от концов отрезка [АВ]
Делим AB
на две равные части: IАСI=IВСI.
Слайд 38
Множество точек, равноудаленных от концов отрезка [АВ]
Прямой угол
проецируется на П1 без искажения, когда его сторона параллельна
П1 (является горизонталью).Из точки С проводим горизонталь h1 А1В1.
Слайд 39 Множество точек, равноудаленных от концов отрезка [АВ] есть
плоскость Σ(h ∩ f) АВ
Прямой угол проецируется на
П2 без искажения, когда его сторона параллельна П2 (является фронталью).Из проекции С2 точки С проводим фронталь f2 А2В1.
Множество точек пространства, равноудаленных от двух точек А и В, есть плоскость СΣ(h ∩ f) АВ, IАСI=IВСI
Слайд 41
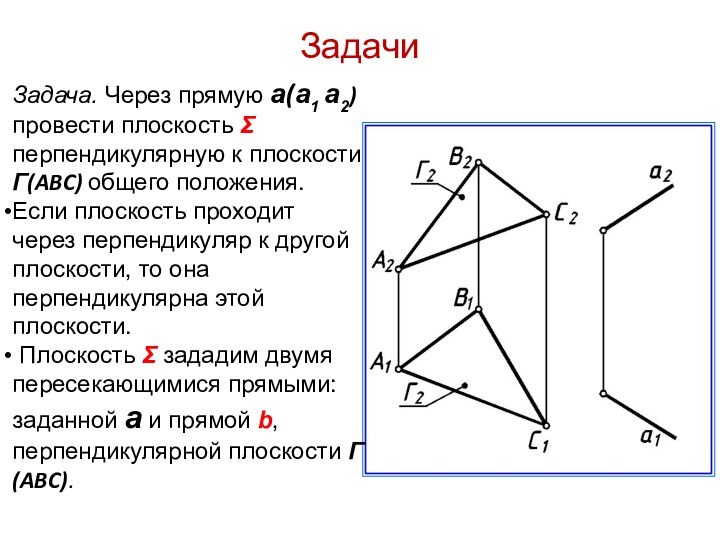
Задачи
Задача. Через прямую а(а1 а2) провести плоскость Σ
перпендикулярную к плоскости Г(ABC) общего положения.
Если плоскость проходит через
перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости.Плоскость Σ зададим двумя пересекающимися прямыми: заданной а и прямой b, перпендикулярной плоскости Г(ABC).
Слайд 42
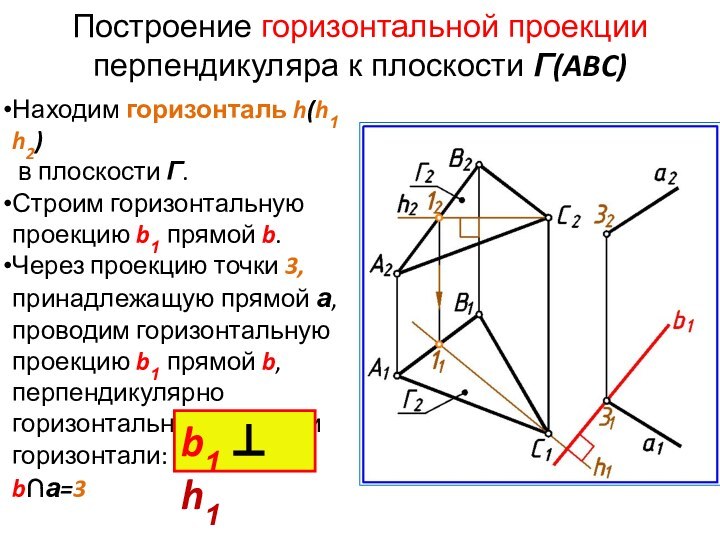
Построение горизонтальной проекции перпендикуляра к плоскости Г(ABC)
Находим горизонталь
h(h1 h2)
в плоскости Г.
Строим горизонтальную проекцию b1 прямой
b.Через проекцию точки 3, принадлежащую прямой а, проводим горизонтальную проекцию b1 прямой b, перпендикулярно горизонтальной проекции горизонтали:
b∩а=3
b1 h1
Слайд 43
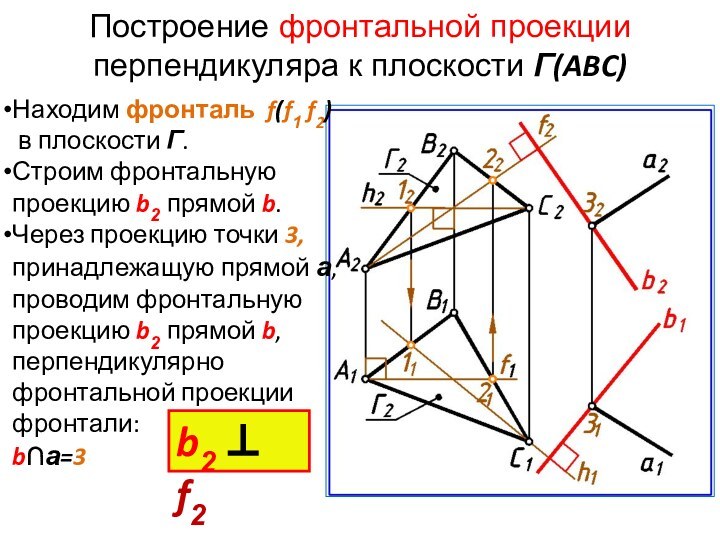
Построение фронтальной проекции перпендикуляра к плоскости Г(ABC)
Находим фронталь
f(f1 f2)
в плоскости Г.
Строим фронтальную проекцию b2 прямой
b.Через проекцию точки 3, принадлежащую прямой а, проводим фронтальную проекцию b2 прямой b, перпендикулярно фронтальной проекции фронтали:
b∩а=3
b2 f2
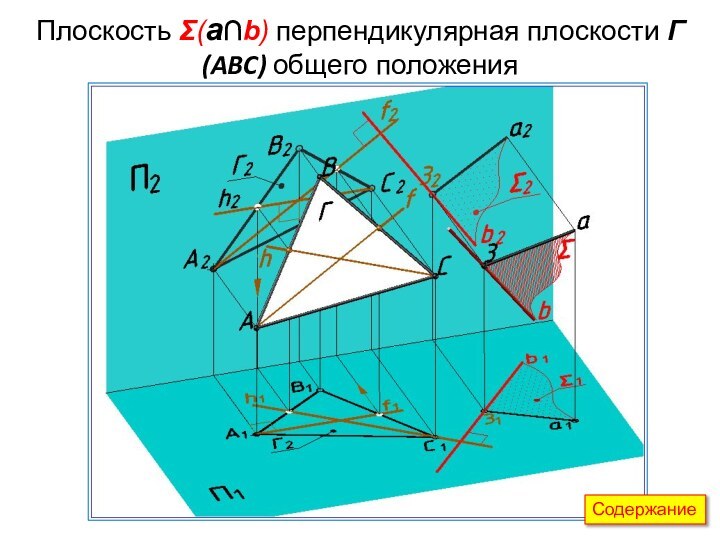
Слайд 44
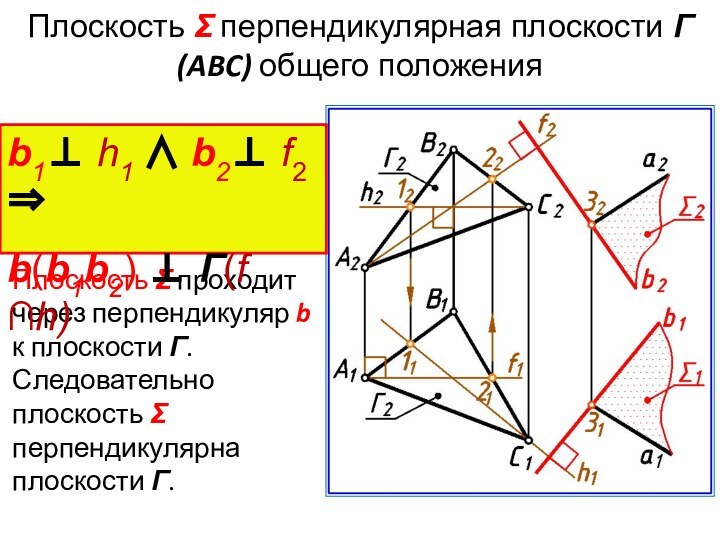
Плоскость Σ перпендикулярная плоскости Г(ABC) общего положения
Плоскость Σ
проходит через перпендикуляр b к плоскости Г. Следовательно плоскость Σ
перпендикулярна плоскости Г.b1 h1 b2 f2
b(b1b2) Г(f ∩h)





























