Слайд 2
Цели урока:
Развивать интуицию
Формировать образное и абстрактное мышление.
Уметь выводить
формулу
(а – b) (a + b) = a2
– b2
Уметь распознавать её в различных ситуациях.
Уметь обобщать и исследовать полученные результаты.
Слайд 3
Изучение нового материала.
Устно:
а) Возведите в квадрат:
8с; 0,9d;
1/4x; 0,05y2 ; 2/7a3
б) Представьте в виде квадрата одночлена:
4a2;
9b4; 16c8; 0,04x10; 0,25x2y2;
0,64x16; 1/9b2
Слайд 4
в) Прочитайте выражения
a – b; a + b;
(a – b) (a + b); a2 – b2;
a2 + b2
г) Решите уравнения:
x2 – 16x =0 и –9 + 2x = 0
д) Разложите на множители:
15x2 y – 10x и x2 –x y2
Слайд 5
Письменно в тетрадях :
Выполните умножение многочленов
a и
b – произвольные:
(a + b) (a – b) =
=a2 + ab – ab – b2=
= a2 – b2
Слайд 6
(a – b) (a + b) = a2
– b2
Формула сокращенного умножения.
Слайд 7
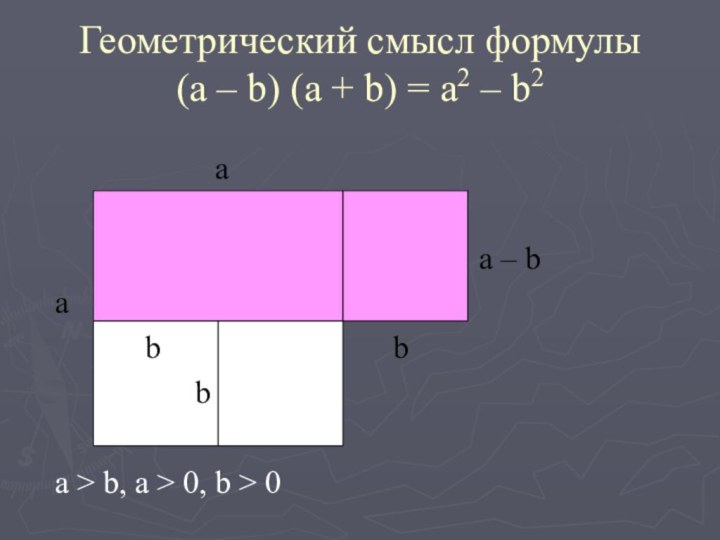
Геометрический смысл формулы
(a – b) (a +
b) = a2 – b2
a
a – b
a
b b
b
a > b, a > 0, b > 0
Слайд 8
Закрепление.
№1. Переставьте выражения в столбцах так, чтобы между
ними можно было поставить знак равно:
(1 + а)(1 –
а) у2 – 9
(у – 3)(у + 3) 1 – а2
(3 – у)(3 + у) 9 – у2
Слайд 9
№2. Выберете выражения, которые могут быть преобразованы по
формуле произведения разности чисел на их сумму, и преобразуйте
их по формуле:
а) (х – у) – (х + у)
б) (b – c) (b + c)
в) (0,2 – х) (0,2 – х)
г) (3 + 2) (3 – 2)
Слайд 10
На основе выполнения этого задания составьте вопросы, выявляющие
сущность данной формулы.
Влияет ли порядок записи выражений в произведении
на результат преобразований в формуле I?
Важен ли порядок записи выражений, входящих в разность, на результат преобразований по этой формуле?
По какому множителю (сумма или разность) удобно составить результат?
Важен ли порядок множителей в произведении?
Слайд 11
Далее самостоятельно на основе полученного опыта формируем алгоритм:
Является
ли выражение произведением.
Является ли один сомножитель – суммой двух
выражений.
Является ли другой сомножитель – разностью этих выражений.
Если это не выполняется, то это выражение не может быть преобразовано по формуле
(a + b) (a – b) = a2 – b2 , а если да, то
Выделить сомножитель – разность.
Записать разность, составленную из квадрата уменьшаемого и квадрата вычитаемого.
Слайд 12
№3. Выполните умножения по составленному алгоритму:
(7х - 2)
(7х + 2)=
(а – 2) (а + 2)=
84 –
76=
103 – 97=
(0,7х + у2) (0,7х – у2)=
(a3 – b2) (a3 + b2)=
(5x2 + 2y3)(5x2 – 2y3)=
Слайд 13
№4. Решите уравнения:
а) (х + 2) (х –
2) – (х – 3)=2
б) 8m(1 + 2m) –
(4m + 3)(4m – 3)=2m
Слайд 14
Устно:
Какие выражения являются разностью квадратов?
а) х2 * (3у)2
б)
а – b
в) х2 – у
г) (2а)2 – b2
д)
а2 – 25b2
е) 152 – 132
ж) а2 – 36
з) 10 – (2/3)2
и) а2 + b2
k) 4a2 – 25b2
Слайд 15
Письменно:
Разложите на множители:
64 – у4=
25m6 – n2=
81 –
a4 b4=
Слайд 16
Решите уравнение:
x2 – 16 = 0
и 4х2 – 9 = 0
Слайд 17
Проверочная работа:
№1) Преобразуйте многочлен:
(k + m) (k –
m)
(3x + 5y) (3x – 5y)
(1/2m2 – n3) (1/2m2
+ n3)
№2) Представьте в виде произведения:
m2 – n2
c2 – 81
0,64х6 – 9у8
№3) Решите уравнения:
(х – 1) (х + 1) – (х – 3)х = 2 и х2 – 25 = 0