Слайд 2
Пример задачи на движение
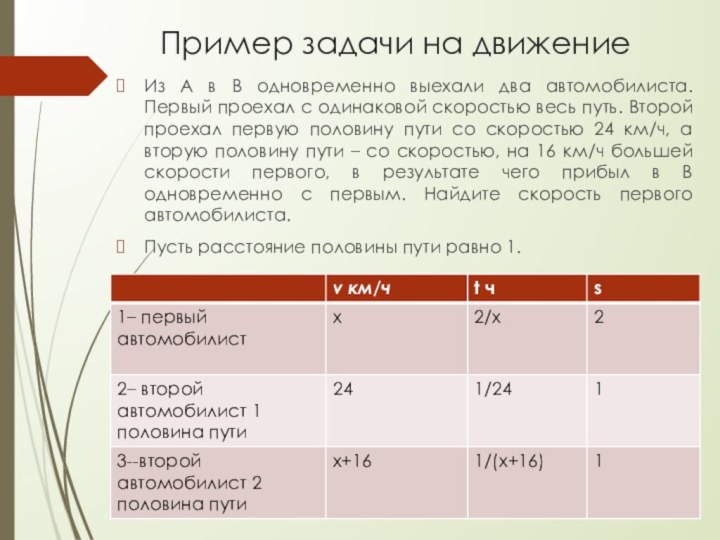
Из А в В одновременно
выехали два автомобилиста. Первый проехал с одинаковой скоростью весь
путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым. Найдите скорость первого автомобилиста.
Пусть расстояние половины пути равно 1.
Слайд 3
Составим и решим уравнение:
1:( x+16)+1:24=2:x
x=32
; x=-24 т.к. скорость не может быть отрицательной, то
x=32 км/ч скорость первого автомобиля.
Ответ: 32 км/ч
Слайд 4
Задача на движение
Велосипедист был в пути 3 часа,
причем за каждый следующий час он проезжал расстояние вдвое
меньше, чем за предыдущий. Какое расстояние проехал велосипедист за последний час, если весь путь составил 49 км?
Ответ выберите из данных:
а) 14 км; б) 28 км; в) 7 км; г) 21 км.
…в)
Слайд 5
Пример задачи на совместную работу
Бак заполняют керосином за
2 часа 30 минут с помощью трех насосов, работающих
вместе. Производительности насосов относятся как 3:5:8. Сколько процентов объёма будет заполнено за 1 час 18 минут совместной работы второго и третьего насосов?
Примем объём бака за 1. Коэффициент пропорциональности равен x.Производительность 1-го—3x; 2-го– 5x; 3-го– 8x. Время совместного наполнения бака равно [ 1:( 3x+5x+8x)=1: 16x] или 2,5 часа. x=1:40. Производительность 2-го—1:8; 3-го—1:5; совместно 2 и 3-го– 13:40; за 1ч 18 мин– [13:40*1,3= 0,4225], что составляет 42,25%.
Ответ: 42,25%
Слайд 6
Задача на совместную работу
Через первую трубу можно наполнить
бассейн на 5 часов быстрее, чем через вторую, а
третья труба наполняет бассейн на 4 часа быстрее первой. За какое время можно наполнить бассейн через третью трубу, если это время равно времени за которое наполняют бассейн первая и вторая труба вместе.
Ответ выберите из данных:
а) 6 ч; б) 7 ч; в) 8 ч; г) 10 ч.
…а)
Слайд 7
Пример задачи на проценты
Свежие фрукты содержат 72% воды,
а сухие -- 20%. Сколько сухих фруктов получается из
20 кг свежих?
В свежих фруктах сухой остаток равен 100%-72%=28%. В 20 кг свежий остаток 20*0,28=5.6 кг. В сухих фруктах сухой остаток равен 100%-20%=80%. 5,6 кг сухого вещества составляют 80% в сухих . 5,6:0,8=7 (кг)
Ответ: 7 кг сухих фруктов.
Слайд 8
Задача на проценты
Влажность сухой цементной смеси на складе
составляет 18%. Во время грузоперевозки из-за дождей влажность смеси
повысилась на 2%. Найдите массу привезённой смеси , если со склада было отправлено 400 кг.
Назовите ответ в кг.
…410
Слайд 9
Пример задачи на сплавы и смеси
Смешали 10%-ный раствор
и 25%-ный раствор соли и получили 3 кг 20%-ного
раствора. Какое количество каждого раствора было взято?
Пусть x(кг)–масса 1 раствора; y(кг)–масса 2 раствора 0,1x(кг)–соли в 1 растворе;0,25y(кг)–соли во 2 растворе
В 3 кг 20%-ного раствора 0,6 кг соли
Составим систему уравнений: x + y=3;
0,1x+0,25y=0,6.
x=1;
y=2.
Ответ: 1 кг, 2 кг.
Слайд 10
Задача на сплавы и смеси
Латунь – сплав меди
и цинка. Кусок латуни содержит меди на 60 кг
больше, чем цинка. Этот кусок латуни сплавили с 100 кг меди и получили латунь, в которой 70% меди. Определите процент меди в первоначальном куске.
Назовите ответ в процентах.
... 60.
Слайд 11
Пример задачи на прогрессии
Отдыхающий по совету врача загорал
в первый день 5 мин, а каждый следующий день
увеличивал время на 5 мин. В какой день недели время пребывания на солнце будет 40 мин, если он начал загорать в среду?
Время пребывания составляет арифметическую прогрессию, первый член равен 5,разность равна 5, n-ый член равен 40. Найдём n.
an =a1 +(n-1)d; 40=5+5(n-1); n=8. a1 – среда, a8 – тоже среда.
Ответ: в среду.
Слайд 12
Задача на прогрессии
Внутренние углы треугольника являются тремя последовательными
членами арифметической прогрессии, у которой разность равна 300. Найти
эти углы.
Покажите решение.
Слайд 13
Решение
… Пусть меньший угол x0 , тогда второй
угол (x+30)0 ,а третий угол (x+30+30)0 Сумма углов
треугольника 1800 . Составим уравнение: x0 + (x+30)0 + +(x+30+30)0 = 1800 .
x=300
Углы равны 300;600;900.
Слайд 14
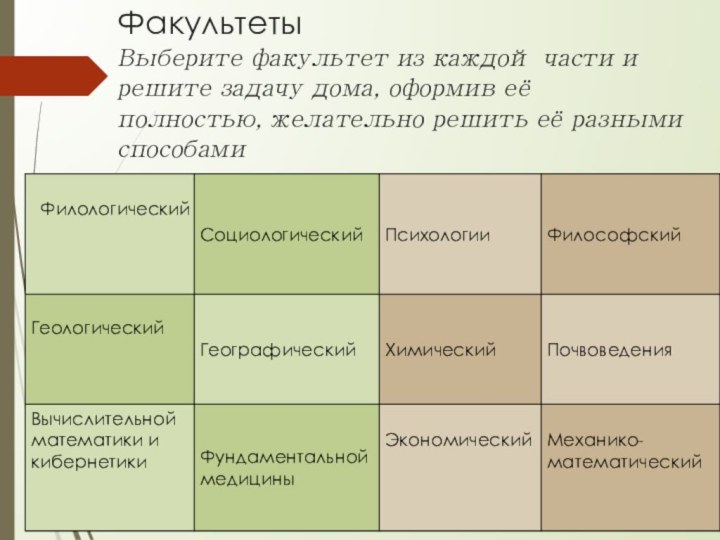
Факультеты
Выберите факультет из каждой части и решите задачу
дома, оформив её полностью, желательно решить её разными способами