Презентация на тему по математике на тему Тригонометрические функции

Содержание

2. Тригонометрические функции — математические функции от угла.
3. В изучении тригонометрических функций можно выделить следующие
4. Существует несколько способов определения тригонометрических функций. Их
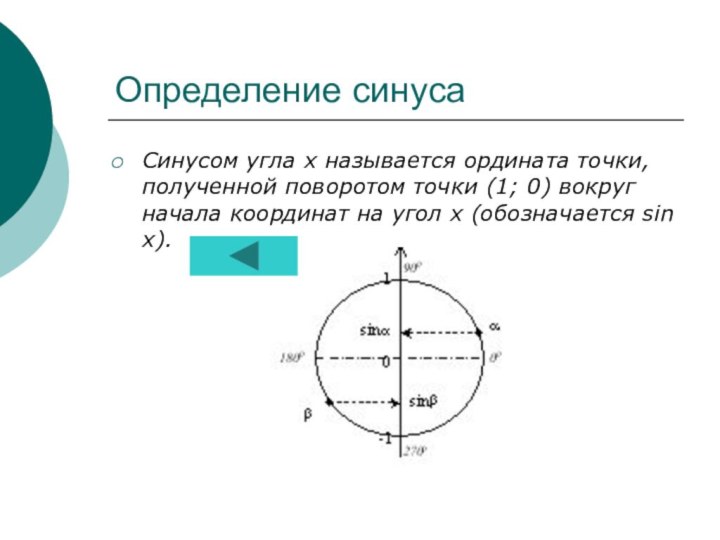
5. Определение синусаСинусом угла х называется ордината точки,
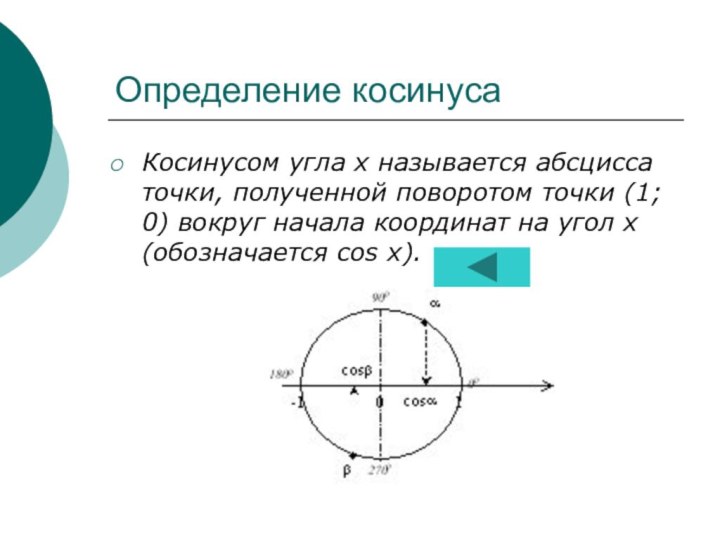
6. Определение косинусаКосинусом угла х называется абсцисса точки,
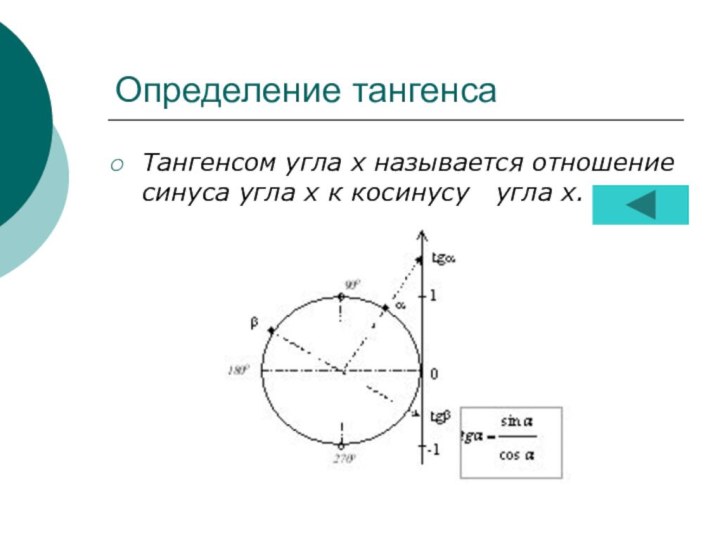
7. Определение тангенсаТангенсом угла х называется отношение синуса угла х к косинусу угла х.
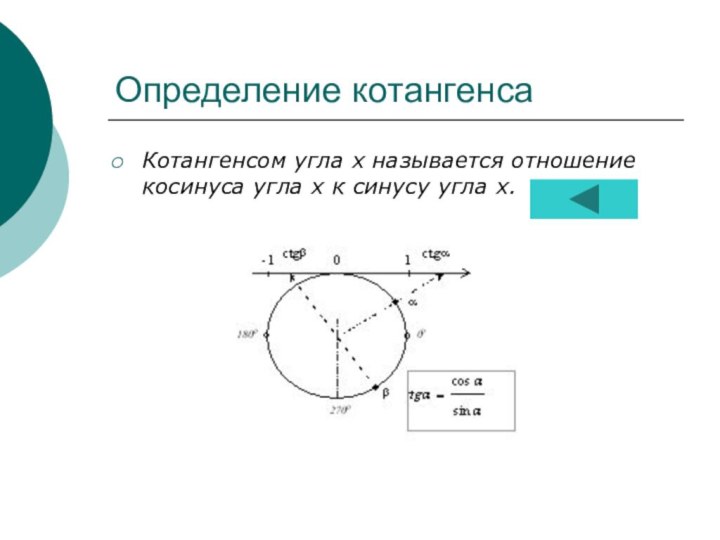
8. Определение котангенсаКотангенсом угла х называется отношение косинуса угла х к синусу угла х.
9. Скачать презентацию
10. Похожие презентации

Тригонометрические функции — математические функции от угла. Они важны при изучении геометрии, а также при исследовании периодических процессов. Обычно тригонометрические функции определяют как отношения сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности. Более современные

Главная
Алгебра
Презентация по математике на тему Тригонометрические функции

ТригонометрическиефункцииПрезентация:Преподавателя ГБПУ ВО «ВАТ имени В.П. Чкалова»Кравцовой Т.Н. на тему: «тригонометрические функции».

Тригонометрические функции — математические функции от угла. Они важны при изучении геометрии,

В изучении тригонометрических функций можно выделить следующие этапы:I. Первое знакомство с тригонометрическими

Существует несколько способов определения тригонометрических функций. Их можно подразделить на две группы:

Определение синусаСинусом угла х называется ордината точки, полученной поворотом точки (1; 0)

Определение косинусаКосинусом угла х называется абсцисса точки, полученной поворотом точки (1; 0)

Определение тангенсаТангенсом угла х называется отношение синуса угла х к косинусу угла х.

Определение котангенсаКотангенсом угла х называется отношение косинуса угла х к синусу угла х.

Обратныетригонометрические функции. Для sin х, cos х, tg х и ctg

Слайды презентации

Слайд 2 Тригонометрические функции —
математические функции от угла. Они

Тригонометрические функции — математические функции от угла. Они важны при изучении

важны при изучении геометрии, а также при исследовании периодических

процессов. Обычно тригонометрические функции определяют как отношения сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности. Более современные определения выражают тригонометрические функции через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на произвольные вещественные числа и даже на комплексные числа.

Слайд 3 В изучении тригонометрических функций можно выделить следующие этапы:
I.

В изучении тригонометрических функций можно выделить следующие этапы:I. Первое знакомство с

Первое знакомство с тригонометрическими функциями углового аргумента в геометрии.

Значение аргумента рассматривается в промежутке (0о;90о). На этом этапе учащиеся узнают, что sin, сos, tg и ctg угла зависят от его градусной меры, знакомятся с табличными значениями, основным тригонометрическим тождеством и некоторыми формулами приведения.
II. Обобщение понятий синуса, косинуса, тангенса и котангенса для углов (0о;180о). На этом этапе рассматривается взаимосвязь тригонометрических функций и координат точки на плоскости, доказываются теоремы синусов и косинусов, рассматривается вопрос решения треугольников с помощью тригонометрических соотношений.
III. Введение понятий тригонометрических функций числового аргумента.
IV. Систематизация и расширение знаний о тригонометрических функциях числа, рассмотрение графиков функций, проведение исследования, в том числе и с помощью производной.

Слайд 4 Существует несколько способов определения тригонометрических функций.
Их можно

Существует несколько способов определения тригонометрических функций. Их можно подразделить на две

подразделить на две группы: аналитические и геометрические.
К аналитическим

способам относят определение функции у = sin х как решения дифференциального уравнения
f (х)=-c*f(х)
или как сумму степенного ряда
sin х = х - х3 /3!+ х5 /5! - …
2. К геометрическим способам относят определение тригонометрических функций на основе проекций и координат радиус-вектора, определение через соотношения сторон прямоугольного треугольника и определения с помощью числовой окружности. В школьном курсе предпочтение отдается геометрическим способам в силу их простоты и наглядности.