Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Урок по алгебре на тему последовательности

Содержание

Рассмотрим ряд чисел: 1, 2, 3, 4, 5, … , n, … (1)
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ, СПОСОБЫ ЕЁ ЗАДАНИЯ И СВОЙСТВАТема урока: Рассмотрим ряд чисел: ОПРЕДЕЛЕНИЕ:Функция натурального аргумента называется числовой последовательностью, а числа, образующие последовательность – членами СПОСОБЫ ЗАДАНИЯ ПОСЛЕДОВАТЕЛЬНОСТИ1) Словесный 1) СЛОВЕСНЫЙ СПОСОБПример 1. Напишем последовательность, состоящую из квадратов чисел натурального ряда. 2) АНАЛИТИЧЕСКИЙ СПОСОБЕсли последовательность задана формулой п-го члена, значит, она задана аналитическим 3) РЕКУРРЕНТНЫЙ СПОСОБПоследовательность задается формулой, по которой вычисляется (п+1)-й член через п-й член.Пример 3. 4) ГРАФИЧЕСКИЙ СПОСОБПример 4. График числовой последовательности состоит Написать все 8 членов данной последовательности ВИДЫ ПОСЛЕДОВАТЕЛЬНОСТИ Конечная РАБОТА ПО УЧЕБНИКУ№ 175, 177, 179 Домашнее задание № 176, 178 вопросы 1-6 стр. 35 Спасибо за урок!
Слайды презентации

Слайд 2 Рассмотрим ряд чисел:

Рассмотрим ряд чисел: 1, 2, 3, 4,

1, 2, 3, 4, 5,

… , n, … (1)

(2)

3, 6, 9, 12, 15, … , n, … (3)

Слайд 3 ОПРЕДЕЛЕНИЕ:
Функция натурального аргумента называется числовой последовательностью, а числа,

ОПРЕДЕЛЕНИЕ:Функция натурального аргумента называется числовой последовательностью, а числа, образующие последовательность –

образующие последовательность – членами последовательности.

(4)

Слайд 4 СПОСОБЫ ЗАДАНИЯ ПОСЛЕДОВАТЕЛЬНОСТИ
1) Словесный

СПОСОБЫ ЗАДАНИЯ ПОСЛЕДОВАТЕЛЬНОСТИ1) Словесный 2) Аналитический


2) Аналитический

3) Рекуррентный
4) Графический

Слайд 5 1) СЛОВЕСНЫЙ СПОСОБ
Пример 1. Напишем последовательность, состоящую из

1) СЛОВЕСНЫЙ СПОСОБПример 1. Напишем последовательность, состоящую из квадратов чисел натурального

квадратов чисел натурального ряда.

1, 2, 3, 4, 5, … , n, … (1)


1, 4, 9, 16, 25, …

Слайд 6 2) АНАЛИТИЧЕСКИЙ СПОСОБ
Если последовательность задана формулой п-го члена,

2) АНАЛИТИЧЕСКИЙ СПОСОБЕсли последовательность задана формулой п-го члена, значит, она задана

значит, она задана аналитическим способом
Пример 2.


при n=3 имеем
при n=6 имеем
при n=8 имеем

Слайд 7 3) РЕКУРРЕНТНЫЙ СПОСОБ
Последовательность задается формулой, по которой вычисляется

3) РЕКУРРЕНТНЫЙ СПОСОБПоследовательность задается формулой, по которой вычисляется (п+1)-й член через п-й член.Пример 3.

(п+1)-й член через п-й член.
Пример 3.

Слайд 8 4) ГРАФИЧЕСКИЙ СПОСОБ
Пример 4.

4) ГРАФИЧЕСКИЙ СПОСОБПример 4. График числовой последовательности состоит из

График числовой последовательности состоит из изолированных точек, абсциссы которых

– натуральные числа, а ординаты значения членов последовательности, номера которых соответствуют этим числам.

Слайд 9 Написать все 8 членов данной последовательности

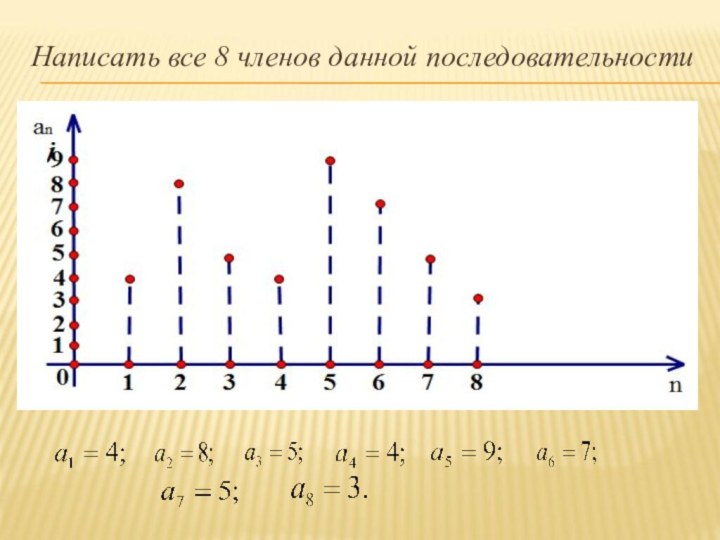
Написать все 8 членов данной последовательности

Слайд 10 ВИДЫ ПОСЛЕДОВАТЕЛЬНОСТИ

ВИДЫ ПОСЛЕДОВАТЕЛЬНОСТИ Конечная

Конечная

Бесконечная
(10, 20, 30, 40, 50, 60, 70, 80, 90) (1, 2, 3, 4, 5,…, п,…)


Возрастающая Убывающая

Постоянная (2, 2, 2, … , 2, …)

Слайд 11 РАБОТА ПО УЧЕБНИКУ
№ 175, 177, 179

Домашнее задание

РАБОТА ПО УЧЕБНИКУ№ 175, 177, 179 Домашнее задание № 176, 178 вопросы 1-6 стр. 35


№ 176, 178 вопросы 1-6 стр. 35

  • Имя файла: urok-po-algebre-na-temu-posledovatelnosti.pptx
  • Количество просмотров: 167
  • Количество скачиваний: 0
- Предыдущая Презентация Технологии добра - опыт работы по созданию и работе волонтёрского отряда в школе
Следующая - Презентация по литературному чтению 3 класс на тему Великие русские писатели

Похожие презентации

Подготовка К ОГЭ-2017 математика 9 класс Подготовка К ОГЭ-2017 математика 9 класс 167
Функции. Графики функций 7 класс Функции. Графики функций 7 класс 184
Решение уравнений Решение уравнений 184
Презентация по теме Логарифмы Презентация по теме Логарифмы 159
Вероятность Вероятность 175
Презентация по математике на тему Расчет статистических данных Презентация по математике на тему Расчет статистических данных 210
Формулы для решения задач на прогрессии Формулы для решения задач на прогрессии 174
Презентация по алгебре на тему Формулы сокращенного умножения Презентация по алгебре на тему Формулы сокращенного умножения 151
Презентация к уроку по теме Решение квадратных неравенств Презентация к уроку по теме Решение квадратных неравенств 149
Дроби 8 класс Дроби 8 класс 183
Презентация по алгебре к уроку по теме Решение задач с помощью пропорций Презентация по алгебре к уроку по теме Решение задач с помощью пропорций 146
Основные понятия дроби Основные понятия дроби 164
Модуль Модуль 199
Производная 10 класс Производная 10 класс 150
Презентация к элективному курсу по математике по теме Процентные расчеты на каждый день (9 класс) Презентация к элективному курсу по математике по теме Процентные расчеты на каждый день (9 класс) 175
Презентация к уроку геометрии Движения. Симметрия в пространстве Презентация к уроку геометрии Движения. Симметрия в пространстве 174
Методы решения систем уравнений Методы решения систем уравнений 169
Приложение к уроку в 8 классе по теме :Теорема Виета Приложение к уроку в 8 классе по теме :Теорема Виета 144
Методы решения тригонометрических уравнений Методы решения тригонометрических уравнений 136
Шаблон игры Игра в математику (3 раунда) Шаблон игры Игра в математику (3 раунда) 156
Прогрессии Прогрессии 186
Презентация по алгебре на тему Решение задач с помощью уравнений 7 класс Презентация по алгебре на тему Решение задач с помощью уравнений 7 класс 175
Основные теоремы дифференциального исчисления Основные теоремы дифференциального исчисления 175
Презентация по математике по теме Арифметическая прогрессия Презентация по математике по теме Арифметическая прогрессия 183
Франсуа Виет Франсуа Виет 146
Шаблоны презентаций ЕГЭ Шаблоны презентаций ЕГЭ 187
Функции и их графики Функции и их графики 405
Презентация к уроку по теме Понятие логарифма Презентация к уроку по теме Понятие логарифма 142
Теорема Виета Теорема Виета 48
Презентация по математике на тему Бірмүше мен көпмүше Презентация по математике на тему Бірмүше мен көпмүше 247