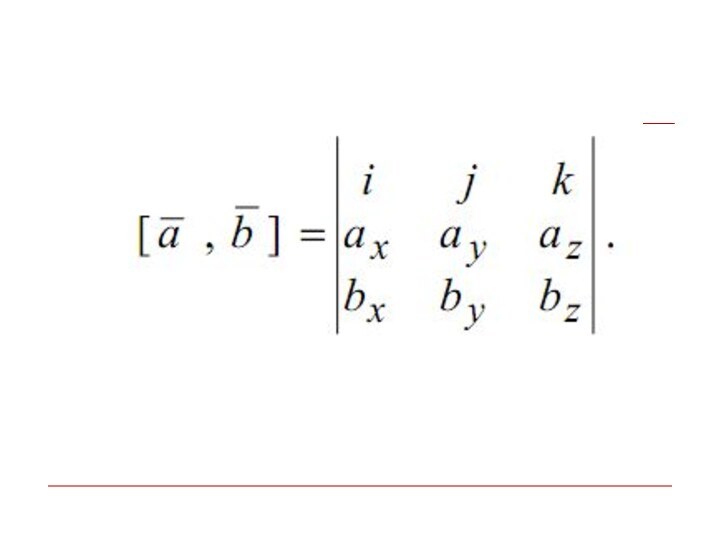- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Векторная алгебра
Содержание
- 2. Векторы Определение. Вектором назовём направленный отрезок,
- 3. Изображение и обозначения
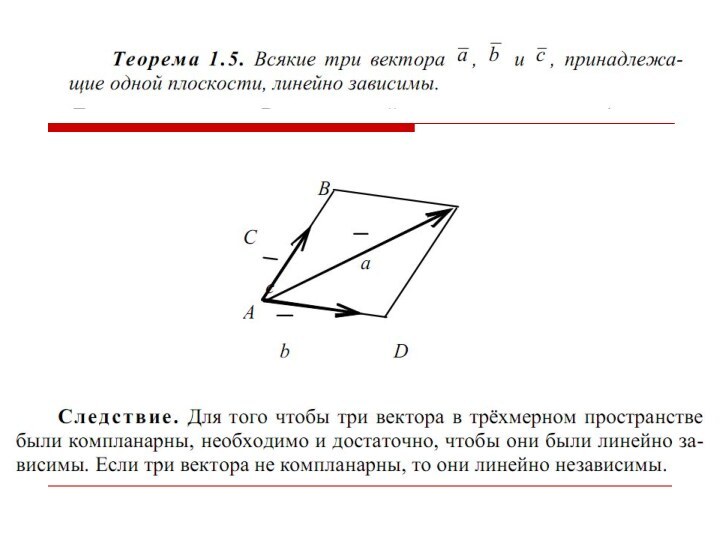
- 6. Компланарные векторыВектор, точка приложения которого может быть выбрана произвольно, называют свободным.
- 7. Линейные операции над векторами К линейным
- 13. Свойства линейных операций над векторами
- 15. Линейная зависимость векторов. Аффинный базис
- 19. Базис на плоскости
- 20. Базис в трехмерном пространстве
- 21. Проекция вектора на ось
- 22. Теоремы о проекциях
- 23. Прямоугольный декартов базис
- 25. Длина вектора
- 26. Длина вектора, заданного концами – расстояние между точками
- 27. Направляющие косинусы вектора Направление вектора в
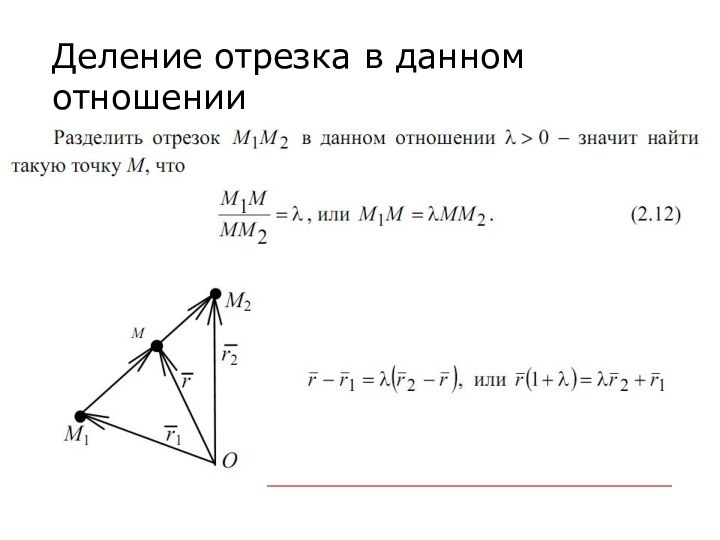
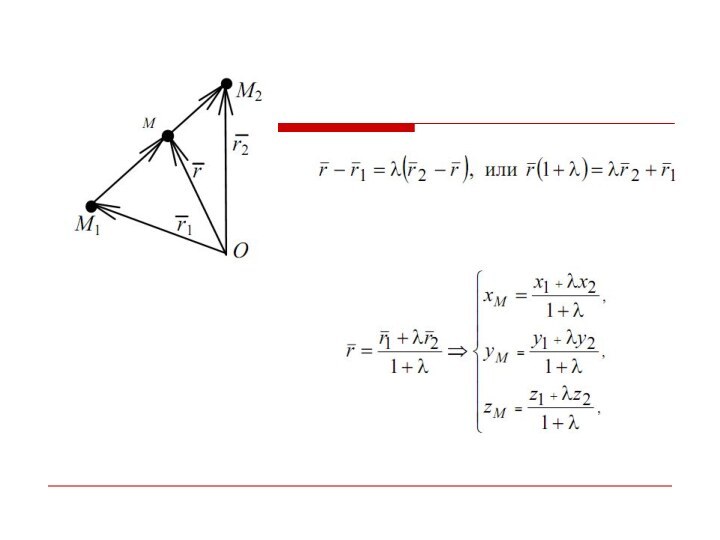
- 29. Деление отрезка в данном отношении
- 31. Скалярное произведение
- 32. Свойства скалярного произведения
- 34. Вычисление проекции вектора на вектор
- 35. Скалярное произведение в декартовой системе координат
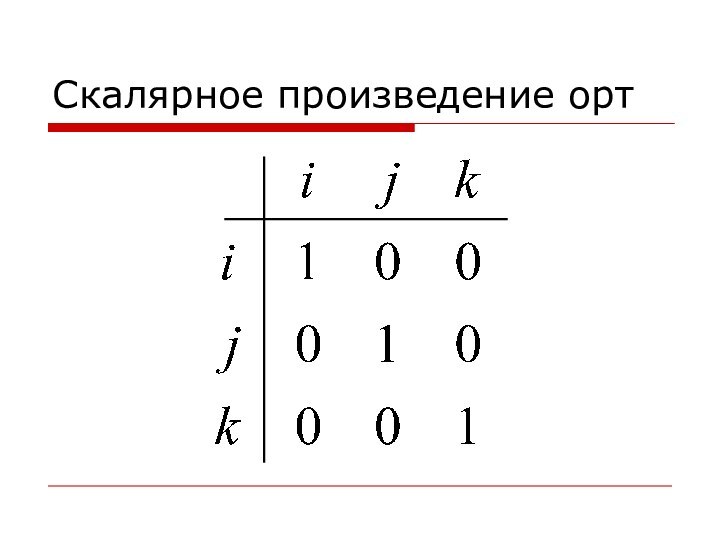
- 36. Скалярное произведение орт
- 37. Скалярное произведение векторов равно сумме произведений их одноименных проекций
- 38. Итоговые формулы
- 39. Векторное произведение
- 40. Модуль векторного произведения
- 41. Основные свойства векторного произведения
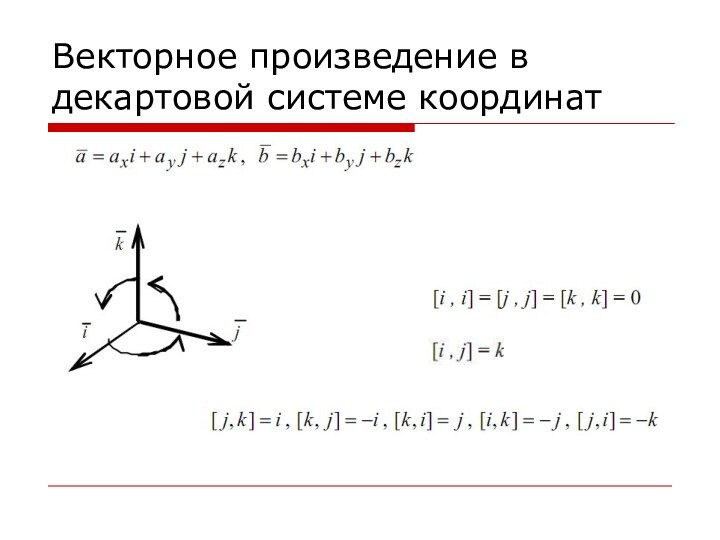
- 43. Векторное произведение в декартовой системе координат
- 44. Векторное произведение орт
- 46. С помощью определения векторного произведения можно решать
- 48. Смешанное произведение трёх векторов
- 49. Смешанное произведение в декартовой системе координатВычислим предварительно векторное произведение
- 51. Геометрический смысл смешанного произведенияПостроим на векторах как на рёбрах параллелепипед
- 53. Вывод: модуль смешанного произведения трёх векторов равен
- 54. Свойства смешанного произведения Все свойства смешанного произведения доказываются с помощью свойств определителя!
- 55. Скачать презентацию
- 56. Похожие презентации
Векторы Определение. Вектором назовём направленный отрезок, т.е. отрезок прямой, ограниченный двумя точками, одна из которых называется начальной, а другая конечной.