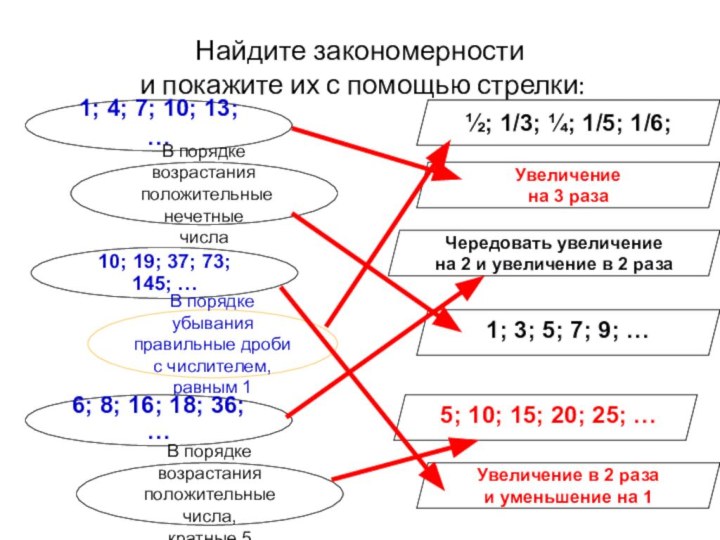
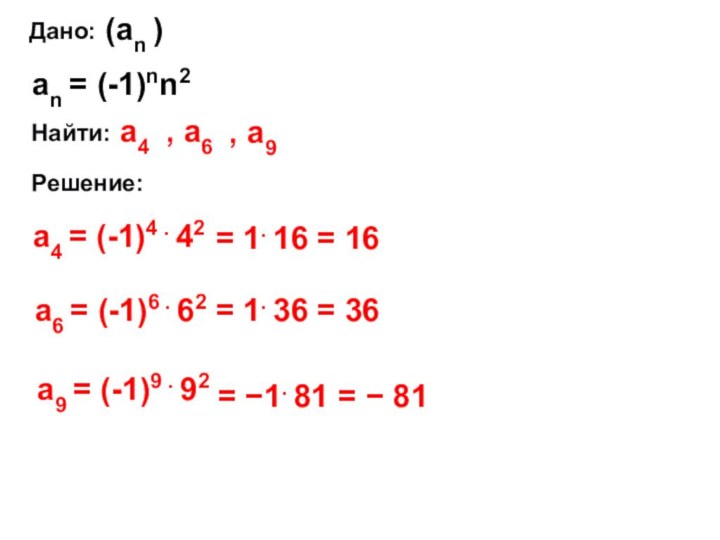последовательности.
2. Какие способы задания числовой последовательности вы знаете? (Приведите
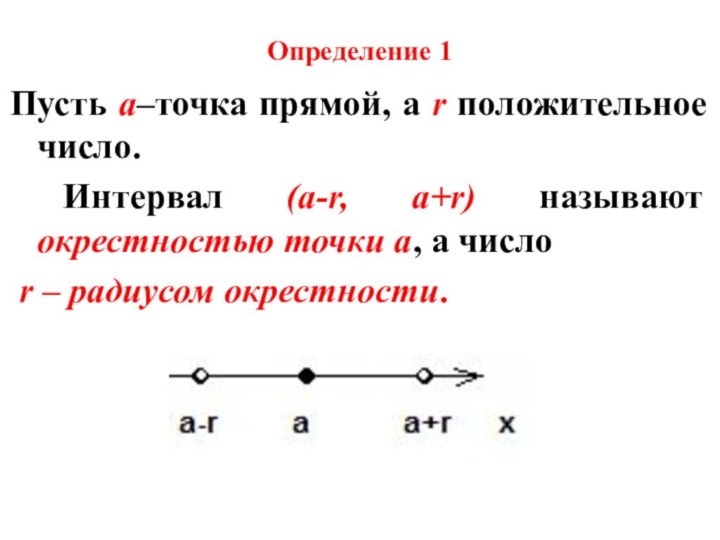
примеры)3. Дайте определение ограниченной сверху и снизу числовой последовательности. (Приведите примеры)
4. Какую последовательность называют возрастающей и убывающей? (Приведите примеры)