Презентация на тему Мастер – класс по математике

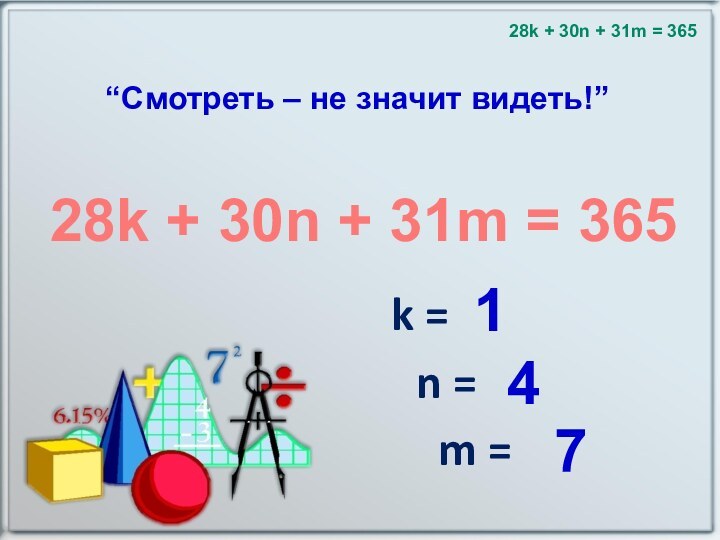
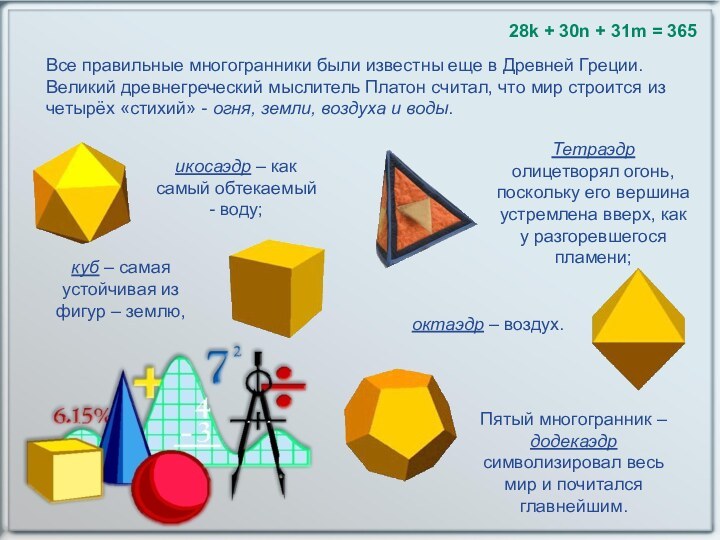
мой друг, суха, но
зеленеет жизни древо.
И.В.Гете

Известно несколько различных способов решения логических задач:

Метод рассуждений;
Метод таблиц;
Метод графов;
Метод блок-схем;
Метод бильярда;
Метод кругов Эйлера.

вызывает сомнение,
но итогом сомнения
может быть озарение!
28k +

30n + 31m = 365

ума через решение задач.
2. Ситуации в жизни такие: либо

сложные, либо простые.
3. Без логики нет математики.
4. В технологию тропинки одолеем без запинки.
5. Точка соприкосновения: “Где же зарыта кошка?”
6. И фокусы покажем,
и секрет расскажем.

28k + 30n + 31m = 365

брат слепой, но у слепого нет
зрячих братьев.

Как это может быть?

11 класс.
Известно, что бумеранг можно бросить
так, что он вернется обратно.
А можно как-то ухитриться
и бросить теннисный мяч так,
чтобы он вернулся обратно?

I этап. Развиваем гибкость ума через решение задач.

28k + 30n + 31m = 365

либо простые
7 класс.
Трём приятелям вручили четыре

яблока. Как, не разрезая и не выбрасывая яблок, разделить их между приятелями так, чтобы каждый получил не больше остальных?

11класс
Какое из чисел больше:
3111 или 1714?

28k + 30n + 31m = 365

В трех мешках находится крупа, вермишель и сахар. На

одном мешке написано “крупа”, на другом “вермишель”, на третьем “крупа или сахар”. В каком мешке что находится, если содержимое каждого для них не соответствует действительности?

11 класс.
Лошадь съедает воз сена за месяц,
коза — за два месяца, овца —
за три месяца.
За какое время лошадь, коза и
овца вместе съедят такой же
воз сена?

28k + 30n + 31m = 365

7класс
В кафе предлагают два первых блюда: борщ,

рассольник и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из первого и второго блюд, которые может заказать посетитель. Проиллюстрируйте ответ, построив дерево возможных вариантов (метод графов)

11класс
В кафе имеются три первых блюда,
пять вторых и два третьих. Сколькими
способами посетитель кафе может
выбрать обед, состоящий из первого,
второго и третьего блюд?

28k + 30n + 31m = 365

Найти величину угла между
биссектрисами смежных и
вертикальных углов.
11класс
Представьте

себе, что вы охватили
земной шар по экватору. А теперь
прибавьте к длине окружности 1 метр
и снова охватите земной шар,
у вас должен получиться зазор.
Пролезет ли кошка через этот зазор?

28k + 30n + 31m = 365

Вопрос:
без чего невозможно
сделать табуретку,
даже

если есть

все-все инструменты
и все-все деревяшки,
гвозди, клей?

28k + 30n + 31m = 365

приходили в храм, то в качестве подношений приносили фигурки,

сложенные из бумаги - оригами. Недаром «ори» означает складывать, а «ками» -«бумага».
Постепенно оригами выходит за пределы храмов. Умение складывать становится одним из признаков хорошего образования. В 19 веке оригами постепенно распространяется по всему миру.
Среди любителей оригами можно
отметить Леонардо да Винчи
и Льюиса Кэролла.
Известно, что Л.Н.Толстой
был знаком с оригами.

28k + 30n + 31m = 365

+ 30n + 31m = 365

Ромбокубооктаэдр
28k + 30n + 31m = 365

30n + 31m = 365

31m = 365

себе лента Мебиуса, у которой один из концов повернули

на 180 градусов и соединили с началом.
Что произойдет, если разрезать по центральной линии ленту Мебиуса?
Сколько она имеет поверхностей: одну или две? Догадливый муравей проверит.
А если красить по поверхности, то лента закрасится с одной стороны или с двух?

n =
m =
28k + 30n

+ 31m = 365

28k + 30n + 31m = 365

1

4

7

огонь, поскольку его вершина устремлена вверх, как у разгоревшегося

пламени;

икосаэдр – как самый обтекаемый - воду;

куб – самая устойчивая из фигур – землю,

октаэдр – воздух.

Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

Все правильные многогранники были известны еще в Древней Греции. Великий древнегреческий мыслитель Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды.

вам в жизни пригодилась математика?
Вопрос детям:
Я изучаю математику, потому

что …