- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Событие. Вероятность события
Содержание
- 2. ТЕМА УРОКА: Событие, вероятность события, сложение и умножение вероятностей. Понятие о независимости событий.
- 3. ПЛАН УРОКА:1. Событие, виды событий2. Вероятность события3.
- 4. «Чтобы в математике решать успешно любую задачу, прежде всего нужно хорошо считать».60, 2830,961,4
- 5. В коробке лежат 3 красных и 5
- 7. ИССЛЕДОВАНИЕ
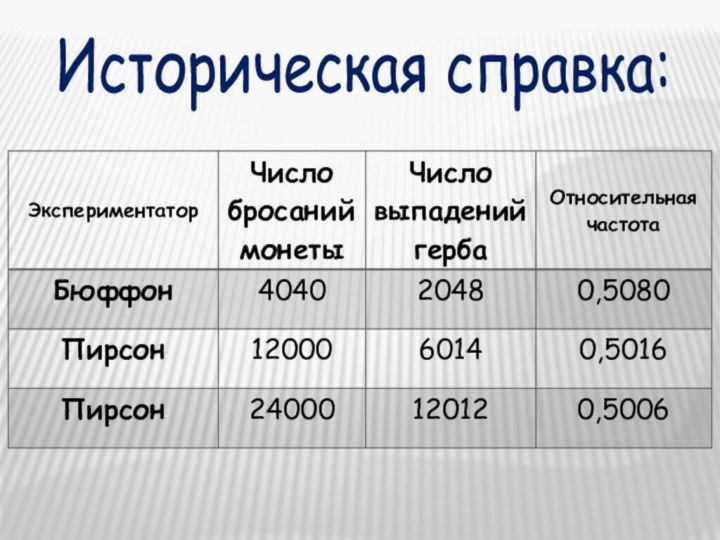
- 8. Историческая справка:
- 9. Эксперимент (опыт) – совокупность условий, при
- 10. ДостоверныеСлучайныеНевозможные
- 11. Теория вероятностей – это раздел математики, изучающий вероятностные закономерности массовых однородных случайных событий.
- 12. Предметом теории вероятностей является изучение закономерностей, которым
- 13. Блез Паскаль(19 июня1623г. – 19 августа 1662г)
- 14. «...В мире господствует случай и одновременно действует
- 15. Задание Среди следующих событий укажите случайные, достоверные,
- 16. Классическое определение вероятности события
- 17. Алгоритм решения задач на расчет вероятности по
- 19. Задача №1.В лотерее из 1000 билетов имеются
- 20. Задача №2.Из урны, в которой находятся 5
- 21. СВОЙСТВА вЕРОЯТНОСТЕЙ СОБЫТИЯ
- 22. Задача №3.На складе имеется 50 деталей, изготовленных
- 23. События А и В называются независимыми, если
- 24. Действия над вероятностями (основные теоремы)
- 25. Задача №4.Прибор, работающий в течении времени t,
- 26. Задача №5.Вероятность попадания в мишень для 1
- 27. Самостоятельная работа
- 29. Домашнее задание
- 30. Достоверное событиеСобытие называется достоверным, если оно обязательно
- 31. НЕВОЗМОЖНОЕ СОБЫТИЕСобытие называется невозможным, если оно не
- 32. СЛУЧАЙНОЕ СОБЫТИЕСобытие называется случайным, если оно может
- 33. Решения к самостоятельной работе
- 34. РЕШЕНИЯ К САМОСТОЯТЕЛЬНОЙ РАБОТЕ
- 35. Скачать презентацию
- 36. Похожие презентации
ТЕМА УРОКА: Событие, вероятность события, сложение и умножение вероятностей. Понятие о независимости событий.


































Слайд 2 ТЕМА УРОКА: Событие, вероятность события, сложение и умножение вероятностей. Понятие
о независимости событий.
Слайд 3
ПЛАН УРОКА:
1. Событие, виды событий
2. Вероятность события
3. Сложение
и умножение вероятностей
4. Понятие о независимости событий
5. Самостоятельная работа
Слайд 4 «Чтобы в математике решать успешно любую задачу, прежде
всего нужно хорошо считать».
6
0, 28
3
0,96
1,4
Слайд 5 В коробке лежат 3 красных и 5 синих
шариков. Какое наименьшее количество шариков, не глядя, нужно достать
из коробки, чтобы среди них обязательно оказалось хотя бы 2 шарика одного цвета?ЗАДАЧА:
Слайд 9 Эксперимент (опыт) – совокупность условий, при которых
рассматривается появление случайного события.
Событие – это ожидаемый результат
эксперимента (наблюдения).Слайд 11 Теория вероятностей – это раздел математики, изучающий вероятностные
закономерности массовых
однородных случайных событий.
Слайд 12 Предметом теории вероятностей является изучение закономерностей, которым подчиняются
случайные события при многократном повторении одного и того же
опыта в одних и тех же условиях.
Слайд 13
Блез Паскаль
(19 июня1623г. – 19 августа 1662г)
французский
математик, физик, философ, один из основателей теории вероятностей
Пьер де
Ферма (17 августа 1601 — 12 января 1665)
французский математик, один из теории вероятностей и теории чисел.
Слайд 14
«...В мире господствует случай и
одновременно действует порядок
и закономерность, которые
формируются из массы
случайностей, согласно законам
случайного»
Из письма Б.Паскаля П.Ферма
Париж, 19 ноября 1654 г,
Г-ну Пьеру Ферма,Тулуза.
Слайд 15
Задание
Среди следующих событий укажите случайные, достоверные, невозможные
события, заполнив при этом таблицу
1. черепаха научится говорить;
2. ваш
день рождения – 19 октября3. день рождения вашего друга – 30 февраля;
4. вы выиграете, участвуя в лотереи;
5. вы не выигрываете, участвуя в беспроигрышной лотерее;
6. вы проиграете партию в шахматы;
7. 1 июля в Новочеркасске будет солнечно;
8. вы выходите на улицу, а навстречу вам идет слон.
9. на следующей неделе наступит апрель;
10. вы нажали на звонок, а он не зазвонил;
11. после четверга будет пятница.
Слайд 17 Алгоритм решения задач на расчет вероятности по классическому
определению
1. Обозначить событие А
2. Найти число возможных исходов -
n3. Найти число исходов, благоприятствующих наступлению события А – m
4. Найти искомую вероятность по формуле:
Слайд 19
Задача №1.
В лотерее из 1000 билетов имеются 200
выигрышных. Вынимают наугад один билет. Чему равна вероятность того,
что этот билет выигрышный?
Слайд 20
Задача №2.
Из урны, в которой находятся 5 белых
и 3 черных шара, вынимают один шар. Найти вероятность
того, что шар окажется черным.
Слайд 22
Задача №3.
На складе имеется 50 деталей, изготовленных тремя
бригадами. Из них 25 изготовлено 1 бригадой, 15 –
2бригадой и 10 – 3 бригадой. Найти вероятность того, что на сборку поступила деталь, изготовленная 2 или 3 бригадой.Слайд 23 События А и В называются независимыми, если появление
события В не оказывает влияния на появление события А,
а появление события А не оказывает влияния на появление события В.
Слайд 25
Задача №4.
Прибор, работающий в течении времени t, состоит
из 3 узлов, каждый из которых, независимо от других,
может в течение времени t отказать (выйти из строя). Отказ хотя бы одного узла приводит к отказу прибора в целом. За время t вероятность безотказной работы 1 узла = 0,8, 2 узла = 0,9, 3 узла = 0,7. Найти надежность прибора в целом.
Слайд 26
Задача №5.
Вероятность попадания в мишень для 1 стрелка
0,85, а для 2 стрелка 0,8. Стрелки независимо друг
от друга произвели по одному выстрелу. Какова вероятность того, что в мишень попадет хотя бы один стрелок?
Слайд 30
Достоверное событие
Событие называется достоверным, если оно обязательно произойдет
в данном опыте.
Например:
Опыт: извлечение мяча из коробки, в
которой находятся только красные мячи.Достоверное событие: «извлеченный, на удачу, мяч окажется красным».
Слайд 31
НЕВОЗМОЖНОЕ СОБЫТИЕ
Событие называется невозможным, если оно не может
произойти в данном опыте.
Например:
Опыт: извлечение мяча из коробки, в
которой находятся только красные мячи.Невозможное событие: «извлеченный, на удачу, мяч окажется зеленым».
Слайд 32
СЛУЧАЙНОЕ СОБЫТИЕ
Событие называется случайным, если оно может произойти,
а может и не произойти в данном опыте.
Например:
Опыт: сдача
студентом экзамена по математике.Случайное событие: «студент на экзамене получит оценку отлично».