Презентация на тему к уроку по алгебре Формулы сокращенного умножения

человеческого гения! В формулах увековечены ценнейшие достижения людского рода,

в них заключено величие и могущество разума, его торжество над покоренной природой.
Из книги “Машина“ под редакцией акад. И.И.Артоболевского

Цель урока:
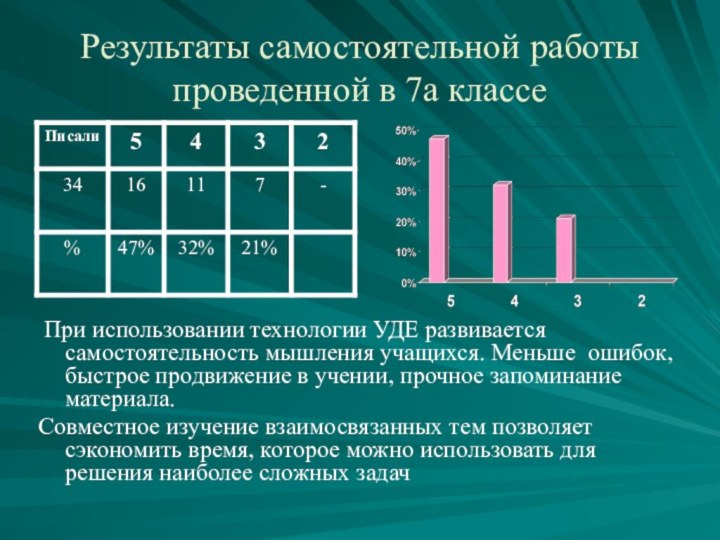
выработать у учащихся умение применять формулы (a±b)2= a2± 2ab+b2 как “слева направо”, так и “справа налево” для преобразования целых выражений и для разложения многочленов на множители.

Цели ученика:
знать формулы (a±b)2= a2± 2ab+b2, уметь читать выражения с переменными, т.е. переходить от формул к их словесному выражению и словесную формулировку записывать формулой, научиться применять эти формулы для преобразования выражений, самостоятельно составлять задания, решать их, выполнять самопроверку.

Средства обучения: средства компьютерных технологий (презентация Power Point), интерактивная доска

Приёмы обучения: приемы технологии УДЕ

выражение и результат, сделайте вывод:
(с+8)2 , (-m-10)2 , (m-n)2

,(7y+6)2 , (12-p)2

воспользовавшись формулами сокращенного умножения.
(a+b)2=
=(a+b)(a+b)=
=(a+b)a+(a+b)b=
=a2+ab+ab+b2=
=a2+2ab+b2
(a-b)2=
=(a-b)(a-b)=
=(a-b)a-(a-b)b=
=a2-ab-ab+b2=
=a2-2ab+b2
Объединяя эти две формулы, мы

можем записать совместно два тождества.
Тождеством называется равенство верное при любых значениях переменных.

(a±b)2= a2±2ab+b2


Читая эти тождества слева направо, получаем формулы сокращенного умножения

(2x+3)2=4x2+12x+9
(7y-6)2=49y2-84y+36

(a±b) (a±b)= a2±2ab+b2


Читая данные тождества справа налево, получаем формулы разложения многочлена на множители

(2x+3)(2x+3)= 4x2+12x+9
(7y-6) (7y-6)= 49y2-84y+36

слагаемых:
квадрата первого числа (a2);

удвоенное произведение первого числа на второе (±2ab);

3) плюс квадрат второго числа (b2).

Схема

a и b




а
а
b
b
=

+


+

(a+b)2

= a2 + 2ab + b2

a и b, удовлетворяющих условию a > b




а
а
b
b
=






-


+

(a-b)2

= a2 - 2ab + b2

таблицу по образцу:

- )∙( -

)=( - )2
25±10b2+b4 =( ± )2

б) +14е +е2 = 72+2∙ ∙е +е2
( - )2= 49 - +е2
( ± )2 =49±14е +е2

Выполните сокращение дробей, запишите пропущенные выражения; проверьте ответ умножением многочленов:

а) 25+ 10а+а2 = =
5+а

б) 25 - 10а+а2 = =
5-а

квадраты чисел и ответы
Образец:
а) б)



в) г)

 b2)2

2. Докажите, что (-а-b)2= (а+b)2

3. Дополните до квадрата

суммы и квадрата разности:
а) а2+2аb + =(а+b)2
б) n2- 4mn + =( - )2
в) 4а6- + b2=( - )2

4. Не выполняя вычислений, сравните значения выражений (28+72)2 и 282+722

5. Вычислите, используя формулы сокращенного умножения:
а) 422
б) 1412-2∙141∙41+412