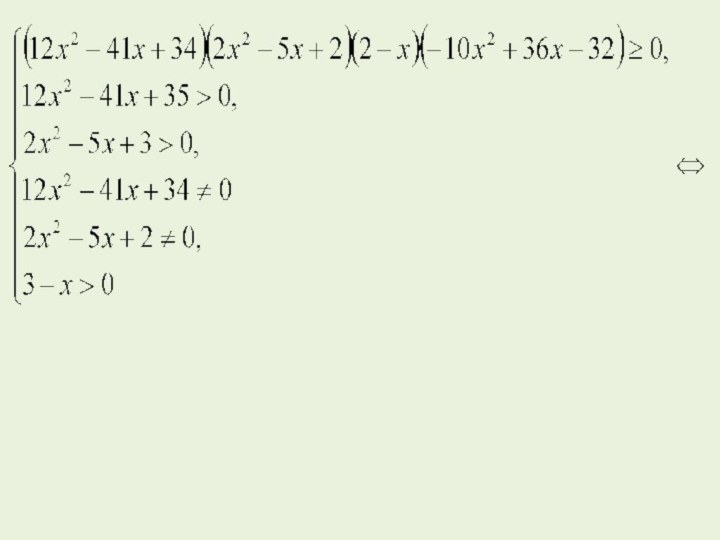Слайд 2
Область применения свойств функции при решении неравенств очень
широка. Наличие свойств (ограниченность, монотонность и т.д.) функций, входящих
в неравенства позволяет применить нестандартные методы решения к стандартным по формулировке задачам – неравенствам. Начнем с примера, связанного с композицией функций.
Пример 28. (МИЭТ, 2002). Пусть
2. Функционально-графические
методы решения
Слайд 3
Решение. Так как,
Так как то неравенство
примет вид
Сделав замену получим систему
Слайд 4
Возвращаясь к переменной x , получим
Слайд 5
2.1. Использование области
определения функции
Предварительный анализ области допустимых значений
неизвестной неравенства иногда позволяет получить решения без преобразований неравенства.
Пример
29. (МИЭТ, 1998). Решите неравенство
Решение. Область определения неравенства задается условием:
Для этих значений x получаем:
Слайд 6
т.е. правая часть исходного неравенства отрицательна на его
области определения. Следовательно, неравенство справедливо при всех
Пример 30. Решите
неравенство
Решение. Область определения неравенства задается условиями:
Слайд 7
Подставляя полученные значения в данное неравенство, получим: при
x = 1 что исходное неравенство примет
Вид т.е. будет
неверно;
при x = 5 имеем верное неравенство
Слайд 8
2.2. Использование непрерывности
функции
Сформулируем свойство непрерывных функций: если функция
f (x) непрерывна на интервале и не обращается в
нуль, то она на этом интервале сохраняет постоянный знак.
На этом свойстве основан метод решения неравенств с одной переменной – метод интервалов. Обобщения метода интервалов связаны с расширением класса функций, входящих в неравенство.
В основе метода интервалов лежат следующие положения:
Слайд 9
Знак произведения (частного) однозначно определяется знаками сомножителей (делимого
и делителя).
2. Знак произведения не изменится (изменится на противоположный),
если изменить знак у четного (нечетного) числа сомножителей.
3. Знак многочлена справа от большего (или единственного) корня совпадает со знаком его старшего коэффициента. В случае отсутствия корней знак многочлена совпадает со знаком его старшего коэффициента на всей области определения
4. Пусть на промежутке (a;b) задана возрастающая (убывающая) функция f (x) , причем x0 – корень уравнения f(x)=0, принадлежащий промежутку (a;b) . Тогда функция f(x) справа от корня положительна (отрицательна), слева отрицательна (положительна), т.е. при переходе через корень меняет знак.
Слайд 10
метод интервалов
Сформулируем свойство чередования знака линейного двучлена при
переходе через
значение знак выражения ax + b меняется
на противоположный. Знание свойства чередования
знака линейного двучлена ax + b позволяет в дальнейшем не приводить линейные двучлены к каноническому виду x = x0 .
Свойство двучлена ax + b лежит в основе метода интервалов и часто используется при решении алгебраических неравенств более высоких степеней.
Слайд 11
Рассмотрим функцию f (x)= f1 (x) f2 (x)
….fn (x), (*)
где fi (x) =aix + bi ,
причем выражения
aix + bi и ajx + bj попарно различны
Выражению (*) соответствует разбиение числовой прямой на интервалы точками
Метод интервалов опирается на следующее свойство чередования знака функции (*): при переходе через точку
Из одного интервала в смежный знак значения функции (*) меняется на противоположный.
Действительно, при переходе через точку
Слайд 12
в выражении (*) меняет знак только один множитель
ai x + b i .
Пример 31. Решите неравенство
Решение.
Перепишем неравенство в следующем виде
и далее используем метод интервалов.
Обозначим
2. D( f ) = R.
3. f (x) = 0;
Отсюда получаем корни уравнения: 1;
Слайд 13
4. Найдем промежутки знакопостоянства функции f (x) .
Так как f (0) > 0 , то расставляем
знаки в соответствии с правилом знакочередования, как показано на рис.
Получаем все значения
при которых f (x) < 0.
Слайд 14
Неравенство
равносильно неравенству f (x)g(x) > 0 (соответственно
f
(x)g(x) < 0 ). Нестрогое неравенство
равносильно системе
На практике неравенство
решают, не приводя
его к виду f (x)g(x) 0, где символ заменяет один из знаков неравенств:
Слайд 16
Так как f (0) > 0 , то
на промежутке (- ;1) функция
f (x) > 0 .
На остальных промежутках расставляем знаки по правилу знакочередования (см. рис.).
Следовательно, f (x) > 0 при всех значениях
x
x
Слайд 17
первое обобщение метода интервалов
Пусть дана функция вида
где fi
(x) = ai x + bi , причем выражения
ai
xi + b и aj x + bj попарно различны
k 1, k2 , ... , kn – фиксированные натуральные числа.
Для решения неравенства f (x) 0 , где выражение f (x) имеет вид (**), используется обобщенный метод интервалов, который опирается на следующее правило чередования знаков выражения: при переходе
через точку из одного интервала
Слайд 18
в смежный знак значения функции (*) меняется на
противоположный, если ki – нечетное число, и не меняется,
если ki – четное число.
Пример 33. Решите неравенство
Решение. 1. Рассмотрим функцию
2. D( f ) = R.
3. Найдем нули функции f (x) из уравнения
Слайд 19
Отсюда x = 3 или x = , или
x = 2,64.
Сравним полученные числа. Так как 7
Аналогично из неравенства
7>2,642=6,9696 получаем
4. Найдем промежутки знакопостоянства функции
f (x) 0. Так как f (0) > 0 , то далее расставляем знаки левой части исходного неравенства, учитывая кратность корней, как показано на рис.
Отсюда f (x) 0 при всех значениях
Слайд 20
второе обобщение метода интервалов
Применимость метода интервалов не ограничивается
решением рациональных неравенств.
Метод интервалов допускает обобщение на выражения вида
где
fi (x) - функции, непрерывные на своей области определения ( i = 1, 2, ... , n; k1 , k2 , ... , kn – фиксированные натуральные числа).
Пример 34. Решите неравенство
Слайд 21
Решение. Так как при x =-1 многочлен x4
+ 4x + 20 принимает наименьшее значение 17 (докажите
с помощью производной), то неравенство x4 + 4x + 20 > 0 выполняется при всех значениях х. Тогда данное
неравенство принимает вид
Используем метод интервалов.
Рассмотрим функцию
2. Функция f (x) не существует при x = 0 и x=log 38 .
Слайд 22
3. Функция f (x) обращается в нуль при
x = 2,5 или
x= log38. Отметим, что в
точке x = 2,5 равны нулю
два множителя
4. Найдем промежутки знакопостоянства функции
f (x) . Так как 0 f (x) 0 при всех значениях
Слайд 23
Пример 35. Решите неравенство
Решение. Обозначим
Тогда данное неравенство примет
следующий вид
Используем метод интервалов.
Рассмотрим функцию
2. Найдем область определения функции
f (t) . Для этого решим неравенство
Слайд 24
3. Находим нули функции f (t) .
Из совокупности
получаем числа 1, 3, 9, нулями функции из которых
являются t = 1 или t =9 , так как 3 D( f ) .
4. Находим промежутки знакопостоянства функции
f (t) . Так как f (0) < 0 , f (10) > 0 , то получаем, что
f (t) 0 при всех значениях
f(t) не
определена
Слайд 25
Полученные решения удовлетворяют условию t 0 . Вернемся
к переменной х.
Замечание. Удобнее в алгоритм решения неравенства (*)
методом интервалов не вносить дополнительное условие t 0 , а учитывать его перед возвращением к
первоначальной переменной.
Слайд 26
рационализация неравенств
При решении неравенств методом интервалов вычисление значений
функций в промежуточных точках может вызвать трудности вычислительного характера.
С другой стороны, для рациональных функций такие вычисления несколько проще.
Чтобы расширить возможности применения метода интервалов при решении неравенств, используем идею рационализации неравенств, известную в математической литературе под другими названиями (метод декомпозиции – Моденов В.П., метод замены множителей – Голубев В.И.).
Слайд 27
Метод рационализации заключается в замене сложного выражения F(x)
на более простое выражение G(x) (в конечном счете, рациональное),
при
которой неравенство G(x) 0 равносильно неравенству F(x) 0 в области определения выражения F(x) .
Выделим некоторые выражения F и соответствующие им рационализирующие выражения G (см. табл. 1), где f , g, h, p, q – выражения с переменной x (h > 0; h 1;
f > 0; g > 0 ), a – фиксированное число ( a > 0; a 1) .
Слайд 29
Некоторые следствия (с учетом области определения неравенства):
В указанных
равносильных переходах символ заменяет один из знаков неравенств:
Слайд 30
Пример 36. Решите неравенство
Решение. Запишем неравенство в виде
и
заменим его равносильной системой, используя метод рационализации
Отсюда получаем решения
Слайд 31
Пример 37. Решите неравенство
Решение. Запишем неравенство в виде
и
заменим его равносильной системой, используя метод рационализации
Знак множителя (|
x + 2 | -1) совпадает со знаком
((x + 2)2 -1) по замене 6.
Слайд 32
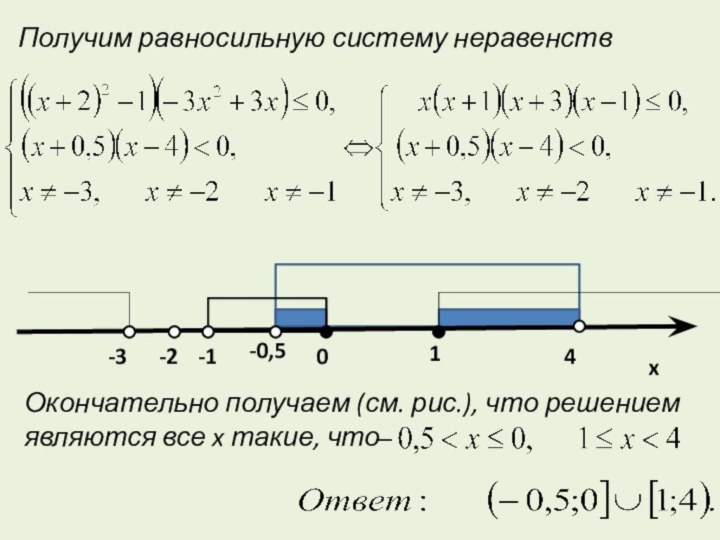
Получим равносильную систему неравенств
Окончательно получаем (см. рис.), что
решением являются все x такие, что
Слайд 33
Пример 38. Решите неравенство
Решение. Заменим данное неравенство равносильной
системой, используя метод рационализации
Слайд 34
Замечание. При решении неравенства (x -1)(x - 2)
< 0 системы учтены условия x > 3, x
> 0, x 1. Условие
1 < x < 2 позволяет исключить множитель x -1 > 0 в
первом неравенстве системы.
Слайд 35
Пример 39. Решите неравенство
Решение. Запишем неравенство в виде
и
заменим его равносильной системой, используя метод рационализации
Слайд 37
Для решения первых трех неравенств системы используем метод
интервалов.
Самостоятельно рассмотрите рисунки и выберите общую часть для решения
системы.
Слайд 38
Пример 40. Решите неравенство
Решение. Область определения неравенства задается
системой
Слайд 39
Учитывая, что при x > 1 выражение log1,9
x положительно, преобразуем данное неравенство на его области определения
Далее
используем метод рационализации
Слайд 41
Решение. Учитывая, что - 3,5 - x >
0, получаем
Далее имеем
Для выяснения взаимного расположения точек на числовой
прямой, сравним числа:
Слайд 42
Получаем
На рис. на числовой оси показано решение первого
неравенства системы.
На рис. на числовой оси показано решение всей
системы.
Слайд 43
метод интервалов на координатной окружности
Данный метод удобно применять
к тригонометрическим неравенствам, приводимым к виду (f 1 (x)-a1)(f2(x)
- a2) ... (f n (x)- an)\/ 0, в частности,
f1 (x ) f2(x ) ... fn(x ) \/0,
где каждая fi (x) – одна из простейших
тригонометрических функций, ai – действительные числа, i=1, 2, ... , n .
В случае, когда наименьший общий период T тригонометрических функций, входящих в данное неравенство, не превосходит 2 ,
Слайд 44
решение неравенства можно рассмотреть на числовой окружности на
промежутке, равном по длине периоду. Далее при записи ответа
следует учесть, что решением данного неравенства будут
являться все числа, отличающиеся от по-
лученных на nT , где n Z .
Пример 42. Решить неравенство
Решение. Для решения неравенства используем метод интервалов.
Пусть
Найдем нули знаменателя
Слайд 45
3. Найдем нули числителя
4. Найдем промежутки знакопостоянства функции
f (x) Так как нули тригонометрических функций (sin x
, sin 3x , cos x , sin2 x ), входящих в данное неравенство, повто-
ряются с периодами
Слайд 46
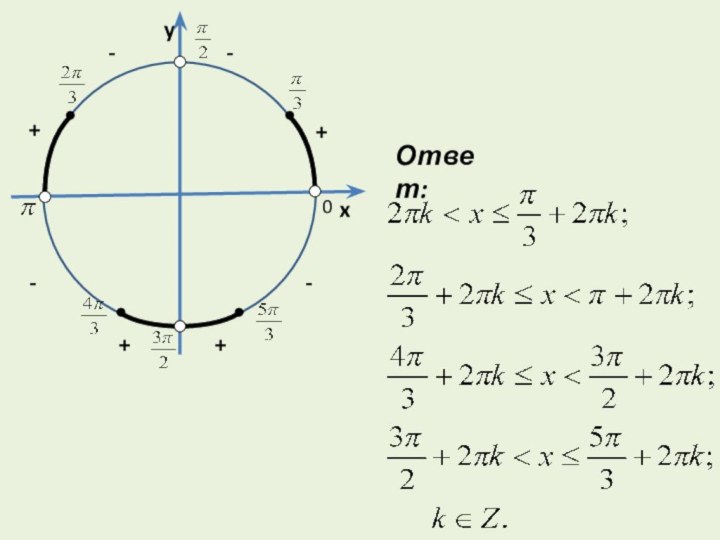
кратными 2 , то изобразим множество решений на
числовой окружности, выделив промежуток [0; 2 ) .
На
промежутке [0; 2 ) функция f (x) не определена в
Точках и обращается в нуль в точках
При этом – точки четной
кратности, остальные – нечетной кратности.
Так как то расставляем знаки в
соответствии с правилом знакочередования, как показано на рис.
Слайд 48
2.3. Использование ограниченности функций
Для использования ограниченности функции необходимо
уметь находить множество значений функции и знать оценки области
значений стандартных функций (например,
метод оценки
Иногда неравенство f (x) \/ g(x) устроено так, что на всей ОДЗ неизвестной имеют место неравенства
при некотором А. В этом случае: а) решение неравенства
сводится к нахождению тех значений x , для которых одновременно f (x) = A и g(x) = A ;
Слайд 49
б) решение неравенства
сводится к нахождению тех решений неравенства
f (x) A, для которых определена функция g(x) .
Пример
43. Решите неравенство
Решение. Область определения неравенства задается
условиями:
Для всех x из полученного множества имеем
Следовательно, решением этого неравенства является промежуток (0;1].