Слайд 2
ЦЕЛЬ
Познакомиться с творчеством художника Мориса Эшера.
Выделить в его
картинах некоторые математические идеи.
- «Автопортрет» (1923).
Слайд 3
«Математика владеет не только истиной,
но и высшей красотой отточенной и строгой, возвышенно
чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства»
Бертран Рассел.
Математик, так же как и художник или поэт, создаёт узоры, и если его узоры более устойчивы, то лишь потому, что они составлены из идей.
Слайд 4
Работы известного голландского художника Мориса Корнемуса Эшера
(1898 – 1971) обладают какой–то магической притягивающей силой. Творчество
Эшера оправдывает многие математические идеи. Так, например, его орнаменты могут напоминать опытному математику о кристаллографических группах.
Слайд 5
Несколько вариаций на тему Эшера
Литография «ВОДОПАД» (1961)г
«Вода всё
время течёт вниз – и бесконечно движется по кругу»
Слайд 6
Литография «Поднимаясь и опускаясь»
Литография
«Поднимаясь и опускаясь» (1960)г
«Монахи идут по замкнутой лестнице: одни всё время вверх,
другие – вниз (бессмысленную работу голландцы называют – «Монашеский труд»).
Слайд 7
«Одним из главных предметов исследования являются такие
объекты, которые локально устроены одинаково, а глобально – по-разному»
Например, окружность и прямая: локально, устроены одинаково (если разрешить изгибание), но в целом – «глобально» – совершенно различны.
Слайд 8
«Лента Мебиуса»
Если бросить из прямой точку, то прямая
распадается на два куска; окружность же остаётся связной. Или
например знаменитая лента Мебиуса
- «Лента Мебиуса» (1963)г.
Слайд 9
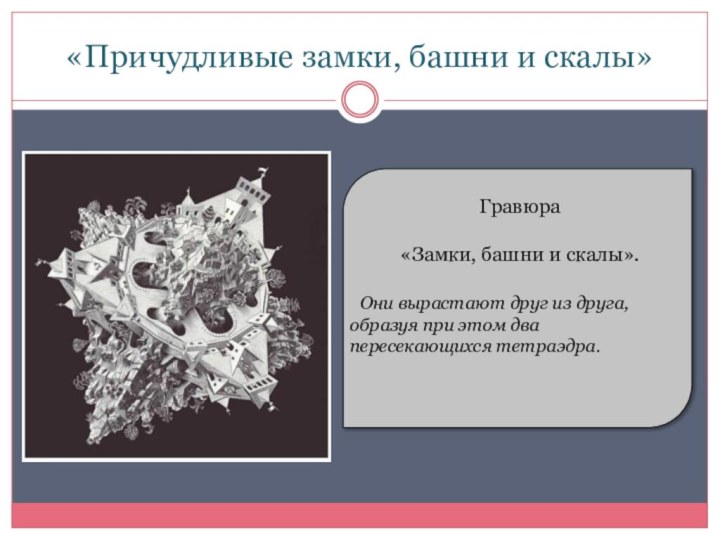
«Причудливые замки, башни и скалы»
Гравюра
«Замки, башни и скалы».
Они вырастают друг из друга,
образуя при этом два пересекающихся тетраэдра.
Слайд 11
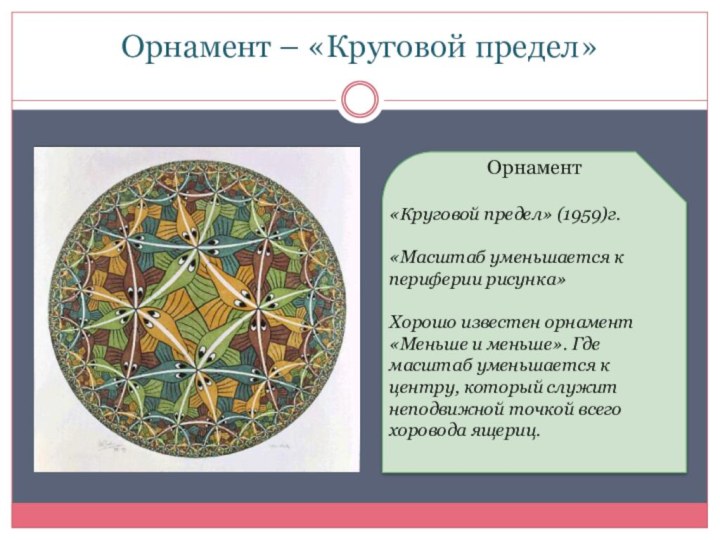
Орнамент – «Круговой предел»
Орнамент
«Круговой предел» (1959)г.
«Масштаб уменьшается к
периферии рисунка»
Хорошо известен орнамент «Меньше и меньше». Где масштаб
уменьшается к центру, который служит неподвижной точкой всего хоровода ящериц.
Слайд 12
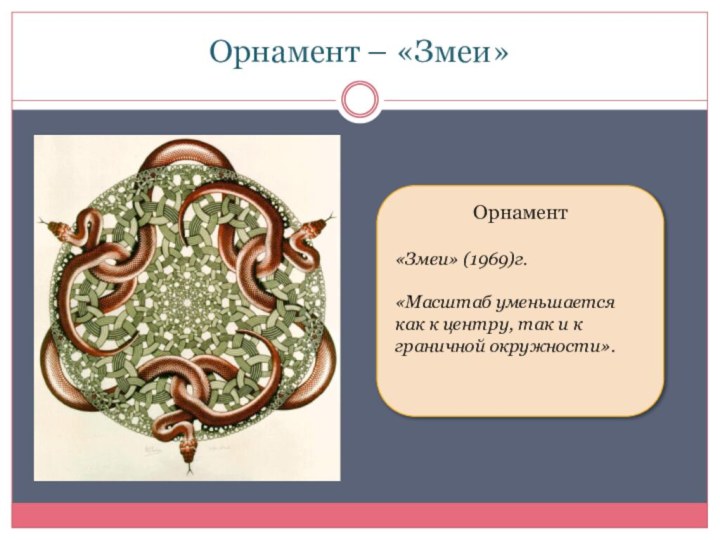
Орнамент – «Змеи»
Орнамент
«Змеи» (1969)г.
«Масштаб уменьшается как к центру,
так и к граничной окружности».
Слайд 13
«Идея о неподвижной точке – одна
из основных в математике:
отображение, уменьшающее масштаб, имеет единственную
неподвижную точку. В действительности неподвижную точку имеет любое непрерывное отображение круга (или шара) в себя».
Слайд 14
«Идея взаимодействия объекта и обозначающего его знака
– это ещё одна математическая идея, которая присутствует в
картинах Эшера. Рисунок, на таких картинах, покидает плоскость и превращается в реальное трёхмерное тело, а затем снова возвращается в плоскость».
Слайд 15
«Рисующие руки»
«Рисующие руки» (1948)г.
Слайд 17
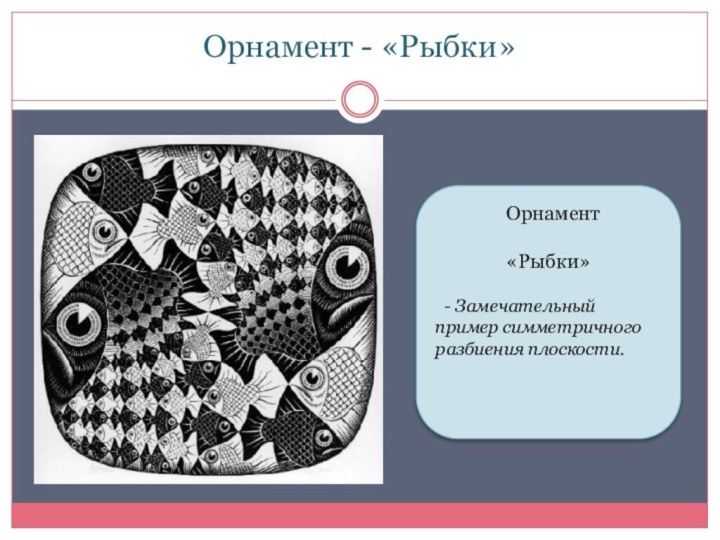
Орнамент - «Рыбки»
Орнамент
«Рыбки»
- Замечательный пример симметричного
разбиения плоскости.
Слайд 18
Орнамент – «Лебеди»
Орнамент
«Лебеди»
Идея: Периодическое заполнение плоскости
одинаковыми фигурами. Повторяющиеся элементы – реальное изображение.
Слайд 19
В итоге можно сказать, что:
«Каждый художник
выбирает те законы и те методы при создании картины,
которые на его взгляд наиболее точно и наиболее красиво передадут его замысел».
Слайд 20
Заключение:
1. Данная работа преследует много целей:
- развивает интерес к изучению математики;
- расширяет кругозор учащихся;
- выделяет математические основы восприятия прекрасного;
- показывает конкретную связь искусства и математики.
2. В процессе исследования данной темы, были выделены математические идеи, которые присутствуют в картинах Мориса Эшера.
3. В перспективе, можно:
- глубже рассмотреть одну из математических закономерностей в работах художника.
- суметь составить программу для построения каких-либо орнаментов или литографии на компьютере.
- продолжать искать математические закономерности в работах современных дизайнеров, в созданиях архитекторов и скульпторов, в творениях природы.