Презентация на тему по алгебре на тему Геометрический смысл производной. Уравнение касательной

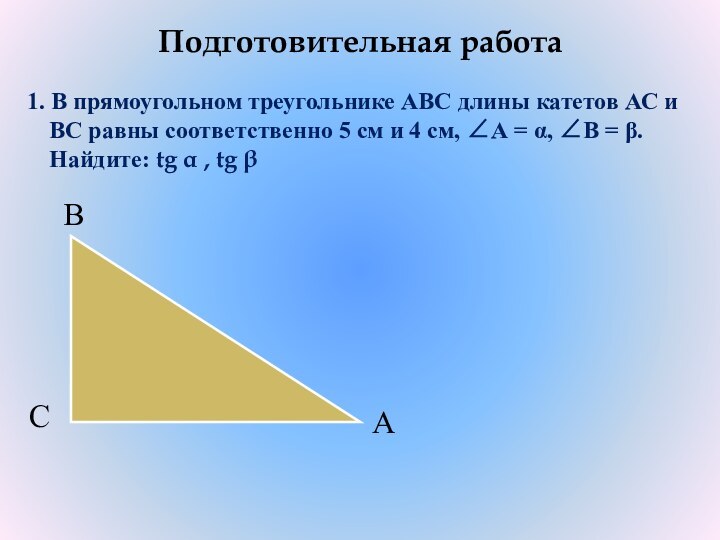
катетов АС и ВС равны соответственно 5 см и

4 см, ∠А = α, ∠В = β. Найдите: tg α , tg β

А

В

С

2, у = -х + 3, отметить угол α

между каждой прямой и положительным направлением оси абсцисс и какую-нибудь точку М на стороне угла α, не лежащей на оси абсцисс.

3. Спроектировать точку М на ось абсцисс и найти tgα.

4. Сделать вывод.

Тангенс угла, образованного прямой у = kx + b и положительным направлением оси абсцисс, равен k.
tg α = k
Число k называется угловым коэффициентом прямой y = kx + b.

с ней, то угол между прямой и осью считается

равным нулю, т. е. в этом случае тангенс угла равен угловому коэффициенту прямой
у = b
у = 0x + b, k =0

Каков характер изменения функции?

Если k > 0, то функция возрастает.
Если k < 0, то функция убывает.
Если k = 0, то функция постоянна.

функции:
а) у = х + 4;
б) у = -2х

+ 1;
в) у = 3;

Найдите угол между прямой и осью абсцисс:
а) у = х + 1;
б) у = -х + 2;

функций:

изменения функций
Охарактеризовать доходы мальчиков

рисунков изображена касательная

= f(x).
Пусть функция y = f(x) определена в некоторой

окрестности точки х0 и существует f′(x0).
Рассмотрим график дифференцируемой функции y = f(x).

В

А

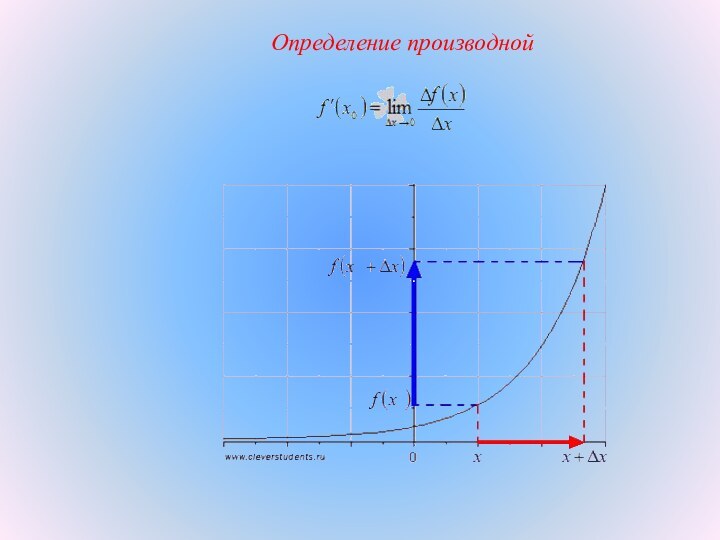
f(x0)

f(x0+h)

x0 + Δх

x0

C

Δх

f(x0+Δх) – f(x0)

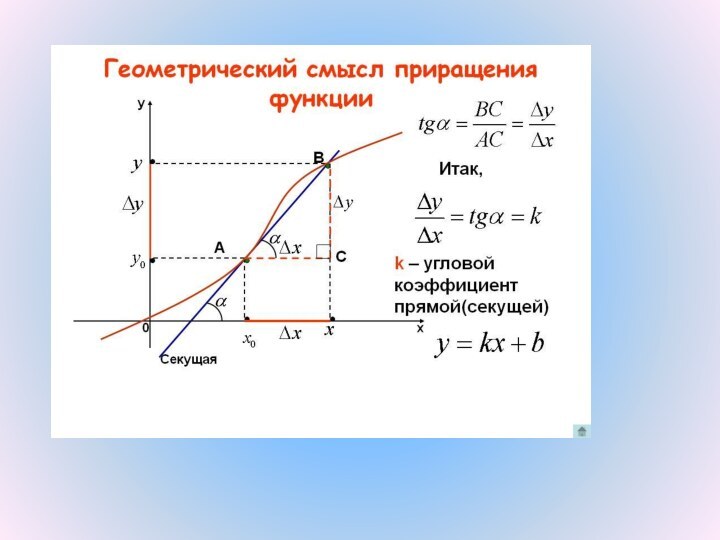
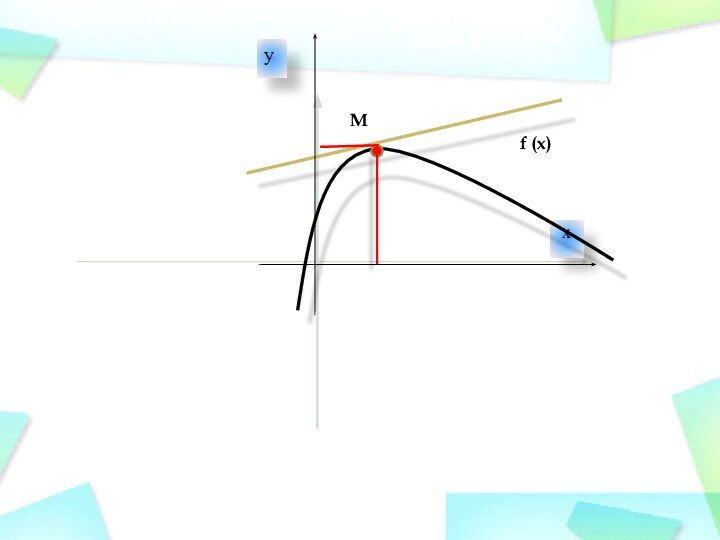
Прямая АВ называется секущей к графику функции y = f(x).
Угловой коэффициент прямой АВ k равен

y = f(x)

двигаясь по графику, приближается к точке А,
а секущая

поворачивается вокруг точки А.
Если существует
т.е. существует предельное положение секущей , то
прямая
называется касательной к графику
функции y = f(x) в точке (х0; f(x0)).
Итак, касательная к графику функции
y = f(x) в точке (х0; f(x0)) − предельное
положение секущей ВА при Δх → 0.

В

А

f(x0)

f(x0+Δх)

x0 + Δх

x0

C

Δх

y = f(x)

то


где α − угол, образуемый касательной с положительным направлением

оси Ох.
Итак,

Геометрический смысл производной
состоит в том, что значение
производной функции f(x) в точке х0
равно угловому коэффициенту
касательной к графику функции
у = f(x) в точке (х0; f(x0)).

В

А

f(x0)

f(x0+Δх)

x0 + Δх

x0

C

Δх

f(x0+Δх) – f(x0)

y = f(x)

в точке с абсциссой х0= - 2.

линейных функций
y = 8х+12 и

y = kх – 3 параллельны.

Ответ: 8.

(а, б)
Учебник 10 – 11 класс / А. Н.

Колмогоров

?
2. В любой ли точке графика можно провести

касательную? Какая функция называется
дифференцируемой в точке?

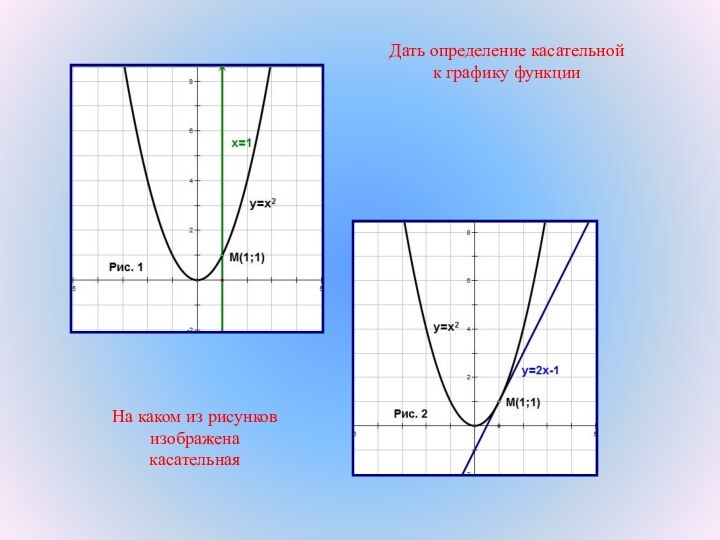
3. Касательная наклонена под тупым углом к
положительному направлению оси Ох.
Что можно сказать о знаке производной и характере монотонности функции?

4. Касательная наклонена под острым углом к
положительному направлению оси Ох.
Что можно сказать о знаке производной и характере монотонности функции?

5. Касательная наклонена под прямым углом к
положительному направлению оси Ох.
Что можно сказать о производной?

180°, α ≠ 90°
α - тупой
tg α

0
f ´(x₀) < 0

α – острый
tg α >0
f ´(x1) >0

положение
касательной не
определено
tg α не сущ.
f ´(x3) не сущ.

α = 0
tg α =0
f ´(x2) = 0

x0) + f(x0)
(x0; f(x0)) – координаты точки касания
f´(x0)

= tgα =k – тангенс угла наклона касательной в данной точке или угловой коэффициент
(х;у) – координаты любой точки касательной

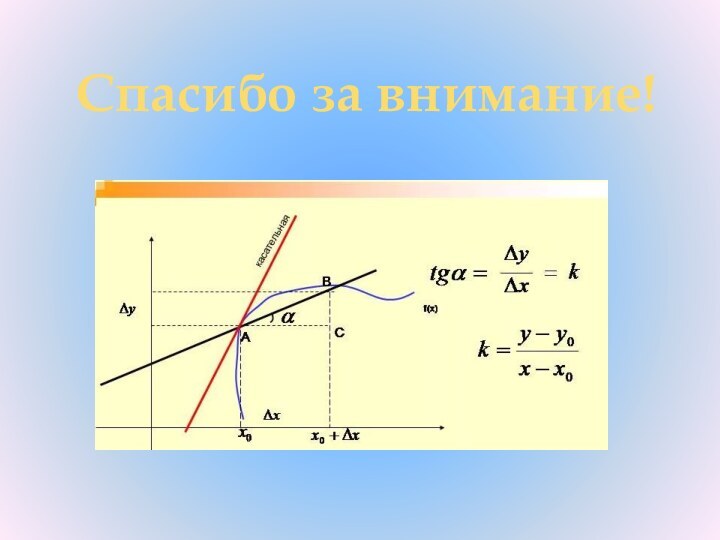
Уравнение касательной

в точке с абсциссой х0= - 2.

10 – 11 класс / А. Н. Колмогоров

257 (в, г)
№ 255 (в, г), 256 (в,

г)
Учебник 10 – 11 класс / А. Н. Колмогоров